32. Опытные законы теплопроводности и внутреннего трения. Коэффициенты теплопроводности и внутреннего трения

1). Внутреннее трение. Это явление переноса наблюдается в том случае, когда в жидкости или газе происходит направленное движение вещества, причем в разных местах скорость движения разная.

Рассмотрим, например, движение жидкости или газа в трубе (рис. 2.13). Вдоль оси трубы модуль скорости _н направленного движения максимален, а вблизи стенок минимален. Градиент модуля скорости направленного

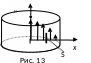движения направлен против оси х (в сторону нарастания модуля _н). Между слоями жидкости (то есть на воображаемую площадку S) параллельную оси трубы) действует сила внутреннего трения. Её величина, в соответствии с опытом, равна (закон Ньютона)

.

Рассмотренное свойство движущихся жидкостей и газов называют также вязкостью.

2). Теплопроводность. Явление теплопроводности имеет место в том случае, когда в системе установлен градиент температуры.

Пусть, например, на противоположных стенках тела поддерживаются разные температуры Т₁ > Т₂ (рис. 14). Градиент температуры всегда направлен в сторону наиболее быстрого её возрастания. Теплота будет передаваться от горячей стенки к холодной (плотность теплового потока направлена в сторону, обратную градиенту температуры).

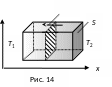Количество перенесенной теплоты Q через площадку S за время t, а также проекция плотности теплового потока j_Q на ось x определяются законом Фурье

,

(36)

Коэффициент теплопроводности , как следует из (36), имеет смысл количества теплоты, переносимой через единичную площадку в единицу времени при градиенте температуры равном единице.

Физические механизмы теплопроводности в газах и твердых телах, как отмечалось, разные. Объяснение явлений переноса в газах мы дадим в следующем параграфе на основе МКТ. Теплопроводность твердых тел рассматривается в одном из заключительных разделов курса физики.

Для коэффициента внутреннего трения в газах МКТ предлагает следующую формулу:

.  Температурная зависимость коэффициента вязкости аналогична зависимости для коэффициента теплопроводности:  , и этот коэффициент, также как и теплопроводность, не зависит от концентрации молекул газа (плотности газа).      Независимость коэффициента вязкости от плотности газа имеет то же объяснение, что и для теплопроводности. С повышением плотности увеличивается число молекул, переносящих импульс, но уменьшаются расстояния, на которые этот перенос осуществляется.

Для коэффициента теплопроводности в газах получается

Из этой формулы следует, что с повышением температуры, коэффициент теплопроводности тоже увеличивается:  . Но в отличие от коэффициента диффузии, этот коэффициент не зависит от концентрации молекул газа.      Эта особенность связана с тем, что в более плотном газе в теплопроводности участвует большее количество молекул. Но при этом, вследствие меньшей длины свободного пробега  , энергия передается на меньшие расстояния. Для более разреженного газа ситуация обратная: в переносе энергии участвует меньшее число молекул, но этот перенос осуществляется на большие расстояния.      Отметим так же, что независимость теплопроводности от концентрации молекул газа справедлива только в том случае, если в нем отсутствует макроскопическое перемешивание, и перенос энергии осуществляется без переноса вещества

В формулах (40) и (41) использованы обозначения:  – плотность газа, с_V – удельная теплоемкость.
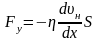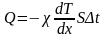