29. Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.

При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям делалось предположение, что внешние силы не действуют на молекулы газа, поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Сила тяжести, с одной стороны, и тепловое движение молекул — с другой, приводят газ к некоторому стационарному состоянию, при котором давление газа с высотой уменьшается.  Выведем закон изменения давления с высотой, предполагая при этом, что масса всех молекул одинакова, поле тяготения однородно и температура постоянна.

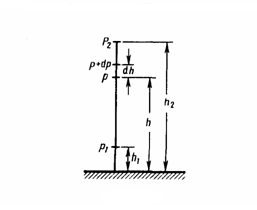Если атмосферное давление на высоте h равно р (рис. 1), то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой уменьшается). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м²:    где ρ — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом интервале плотность газа можно считать постоянной). Значит,   (1)  Зная уравнение состояния идеального газа pV=(m/M) RT (m — масса газа, М — молярная масса газа), находим, что    Подставив это выражение в (1), получим   или    С изменением высоты от h₁ до h₂ давление изменяется от р₁ до р₂ (рис. 67), т. е.    или   (2)  Выражение (2) называется барометрической формулой. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту: Так как высоты считаются относительно уровня моря, где давление считается нормальным, то выражение (2) может быть представлено в виде   (3)  где р — давление на высоте h.  Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на применении формулы (3). Из этой формулы следует, что чем тяжелее газ, тем давление с высотой убывает тем быстрее.  Барометрическую формулу (3) можно преобразовать, если воспользоваться формулой p=nkT:    где n – концентрация молекул на высоте h, n₀ – то же, на высоте h=0. Так как M=m₀N_A (N_A – постоянная Авогадро, m₀ – масса одной молекулы), a R=kN_A, то   (4)  где m₀gh=P — потенциальная энергия молекулы в поле тяготения, т. е.   (5)  Выражение (5) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.  Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и , то распределение Больцмана (5) применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести

30) Среднее число столкновений и средняя длина свободного пробега молекул.

Средние скорости молекул, газа очень велики - порядка сотен метров в секунду при обычных условиях. Однако процесс выравнивая неоднородности в газе вследствие молекулярного движения протекает весьма медленно. Это объясняется тем, что молекулы при перемещении испытывают соударения с другими молекулами. При каждом соударении скорость молекулы изменяется по величине и направлению. Вследствие этого, скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения. Для оценки скорости движения молекул вводится понятие средней длины свободного пробега. Таким образом, средняя дли свободного пробега   - это среднее расстояние, которое проходит молекула от столкновения до столкновения.

Для определения   вычислим сначала среднее число соударений   выбранной молекулы с другими молекулами за единицу времени. Будем считать, что молекула после соударения продолжает двигаться по прямой со средней скоростью движения   .

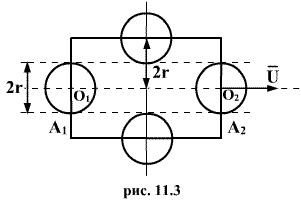
Молекулы, с которыми соударяется выбранная молекула, в первом приближении считаем неподвижными и принимаем их за сферические тела радиуса r. Пусть выбранная молекула движется вправо из положения   в положение   по прямой   (рис.11.3). При своем движении она испытывает соударения с теми неподвижными молекулами, центры которых лежат не дальше чем 2r от траектории   . Иными словами, движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной   , т.е.

.

Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное

Это число   и определяет среднее число соударений за единицу времени.

Предположение о том, что все молекулы, кроме одной, неподвижны, является, конечно не верным. В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости   должны входить средняя относительная скорость молекул   . Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в   раз превышает   . Таким образом, среднее число соударений должно быть увеличено в   раз

(11.7)

Средний путь, проходимый молекулой за единицу времени, численно равен   . Поэтому средняя длина свободного пробега равна   или

(11.8)

Таким образом, средняя длина свободного пробега   не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают и   , и   . При подсчете числа соударений и средней длины свободного пробега молекул за модель молекулы было принято шарообразное упругое тело. В действительности каждая молекула представляет собой сложную систему элементарных частиц и при рассмотрении упругого соударения молекул имелось в виду, что центры молекул могут сблизиться до некоторого наименьшего расстояния. Затем возникает силы отталкивания которые вызывают взаимодействие, подобное взаимодействию при упругом ударе. Среднее расстояние между центрами молекул, взаимодействующих, как при упругом ударе, называют эффективным диаметром   . Тогда

(11.9)