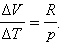- •1.Механическое движение как простейшая форма движения материи. Преставления о формах пространства и времени, лежащие в основе классической механики. Границы применимости классической механики.
- •2. Элементы кинематики материальной точки. Скорость и ускорение точки, как производные радиуса вектора по времени.
- •Кинематические уравнения движения
- •3) Нормальное и тангенциальное ускорения. Радиус кривизны траектории.
- •4.Элементы кинематики вращательного движения. Угловая скорость и угловое ускорение их связь с линейными скоростями и ускорениями точек вращающегося тела.
- •5. Динамика материальной точки и поступательного движения твёрдого тела. Сила. Закон инерции и инерциальные системы отсчета. Закон динамики материальной точки (2 и 3 законы Ньютона)
- •7.Работа консервативных и неконсервативных сил. Определение работы через интеграл, графически и через изменение энергии.
- •8. Кинетическая и потенциальные энергии. Понятие о градиенте потенциала. Закон сохранения механической энергии. Диссипация энергии. Консервативные и неконсервативные силы.
- •9. Поле как форма материи, осуществляющая силовое взаимодействие между частицами вещества. Вес и невесомость. Потенциальная энергия тяготения.
- •10. Применение законов сохранения к абсолютно неупругому удару. Энергия идущая на деформацию. Примеры неупругого удара.
- •11. Применение законов сохранения к абсолютно упругому удару. Частные случаи и их конкретные проявления.
- •12. Динамика вращательного движения абсолютно твердого тела. Момент силы. Основной закон вращательного движения. Момент инерции.
- •13.Момент инерции. Зависимость момента инерции твердого тела от его характеристик. Теорема Штейнера и ее применение на конкретном примере
- •14. Кинетическая энергия вращательного движения. Закон сохранения момента импульса и его проявление.
- •15. Неинерциальные системы отсчета. Силы инерции в поступательно движущейся неинерциальной системе. Эквивалентность сил инерции и гравитационных сил.
- •16. Силы инерции во вращающейся системе отсчета и их применение. Сила Кориолиса.
- •17. Преобразование координат Галилея. Механический принцип относительности. Закон сложения скоростей. Инварианты преобразования.
- •18. Постулаты специальной теории относительности. Преобразования Лоренца. Относительность одновременности.
- •20. Элементы релятивистской динамики. Закон взаимодействия массы и энергии. Изменение массы тела со скоростью. Границы применимости классической механики.
- •Релятивистский импульс
- •Закон взаимосвязи массы и энергии
- •Изменение массы тела со скоростью
- •Закон сложения скоростей
- •21) Термодинамический и молекулярно-кинетический методы исследования. Термодинамические параметры. Равновесные состояния и процессы, и их изображение на термодинамической диаграмме.
- •23. Число степеней свободы молекул. Закон равномерного распределения энергии по степеням свободы молекул. Внутренняя энергия идеального газа.
- •24) Работа газа при изменении его объема. Количество теплоты. Теплоемкость.
- •25.Первое начало термодинамики и применение его к изопроцессам. Работа в изопроцессах.
- •26. Применение первого начала термодинамики к адиабатному процессу. Уравнение Пуассона. Работа газа в адиабатном процессе.
- •27) Теплоемкость. Зависимость теплоемкости идеального газа от вида процесса. Свободная и связанная энергия.
- •28.Закон Максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная квадратичная и средняя арифметическая скорости молекул. Опытное подтверждение.
- •Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.
- •30) Среднее число столкновений и средняя длина свободного пробега молекул.
- •31.Явления переноса в термодинамически неравновестных системах. Коэффициент диффузии
- •32. Опытные законы теплопроводности и внутреннего трения. Коэффициенты теплопроводности и внутреннего трения
- •33) Обратимые и необратимые процессы. Круговые процессы (циклы) и их изображение на термодинамической диаграмме. Принцип Томпсона. Тепловые двигатели и холодильные машины.
- •34.Принцип Томсона. Цикл Карно и его кпд, работа за цикл. Ход цикла Карно в термодинамической диаграмме.
- •35.Второе начало термодинамики. Молекулярно-кинетическая картина равновесных состояний. Энтропия идеального газа.
- •36) Отступление от законов идеальных газов. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.
- •37.Уравнение Ван-дер-Вальса
- •38.Сравнение изотерм Ван-дер-Ваальса с экспериментальными. Критическое состояние.
- •39) Фазовые переходы I и II рода. Уравнение Клапейрона-Клаузиуса.
27) Теплоемкость. Зависимость теплоемкости идеального газа от вида процесса. Свободная и связанная энергия.
Теплоёмкость. Зависимость теплоёмкости идеального газа от вида процесса.
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
|
Во многих случаях удобно использовать молярную теплоемкость C:
|
где M – молярная масса вещества.
Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.
Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp –молярная теплоемкость в изобарном процессе (p = const).
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
|
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
|
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
|
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
pV = RT, |
где R – универсальная газовая постоянная. При p = const
|
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
Cp = CV + R. |
Молярная теплоемкость Cp газа в процессе с постоянным давлением всегда больше молярной теплоемкости CV в процессе с постоянным объемом (рис. 3.10.1).
|
Рисунок 3.10.1. Два возможных процесса нагревания газа наΔT = T2 – T1. При p = const газ совершает работуA = p1(V2 – V1). Поэтому Cp > CV |
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
|
В частности, это отношение входит в формулу для адиабатического процесса .
Свободная и связанная энергия.
В обратимом процессе
|
|
|
|
Это равенство можно переписать в виде
|
|
|
|
Обозначим: ![]() ,
где F – разность двух функций состояний,
поэтому сама является также функцией
состояния. Ее назвали свободной
энергией.
Тогда
,
где F – разность двух функций состояний,
поэтому сама является также функцией
состояния. Ее назвали свободной
энергией.
Тогда
|
|
|
(6.6.1) |
Если тело совершает обратимый изотермический процесс, то
|
|
|
|
|
|
|
|
т.е. ![]() . Следовательно, свободная
энергия есть
та работа, которую могло бы совершить
тело в обратимом изотермическом процессе,
или свободная энергия есть максимальная
возможная работа, которую может совершить
система, обладая каким-то запасом
внутренней энергии. Внутренняя
энергия системы U равна
сумме свободной (F)
исвязанной энергии (TS):
. Следовательно, свободная
энергия есть
та работа, которую могло бы совершить
тело в обратимом изотермическом процессе,
или свободная энергия есть максимальная
возможная работа, которую может совершить
система, обладая каким-то запасом
внутренней энергии. Внутренняя
энергия системы U равна
сумме свободной (F)
исвязанной энергии (TS):
|
|
|
(6.6.2) |
Связанная энергия – та часть внутренней энергии, которая не может быть превращена в работу, – это обесцененная часть внутренней энергии. При одной и той же температуре связанная энергия тем больше, чем больше энтропия. Таким образом, энтропия системы есть мера обесцененности ее энергии (т.е. мера той энергии, которая не может быть превращена в работу). В термодинамике есть еще понятие – энергетическая потеря в изолированной системе:
|
|
|
(6.6.3) |
где Tмин - температура окружающей среды.
При любом необратимом процессе энтропия увеличивается до того, пока не прекратятся какие-либо процессы, т.е. пока не станет F = 0. И это произойдет при достижении замкнутой системой равновесного состояния, т.е. когда все параметры состояния системы (Р, Т) во всех точках системы станут одинаковыми. Вывести систему из этого равновесного состояния, можно только затратив энергию извне.