25.Первое начало термодинамики и применение его к изопроцессам. Работа в изопроцессах.
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
а) изохорный процесс (V= const). Диаграмма этого процесса (изохора) в координатах P и Vизображается прямой, параллельной оси ординат. При изохорном процессе газ не совершает работу над внешними телами, т.е.dA = PdV=0, dQ =dU. Учитывая, что dUμ =CvdT, получаем для произвольной массы газа
.
б) изобарный процесс (P=const). Диаграмма этого процесса (изобара) в координатах P,Vизображается прямой, параллельной оси V.При изобарном процессе работа газа при расширении объёма от V1 до V2 равна
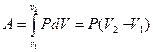
и определяется площадью прямоугольника. Используя уравнение Менделеева – Клапейрона для выбранных нами двух состояний PV1 = mRT1/µ и PV2 = mRT2/µ , имеем V2 – V1 = mR(T2 – T1)/Pµ. Тогда выражение (3.12) для работы изобарного расширения примет вид
.
Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 – T1 = 1K, то для одного моля газа R = A, т.е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1К.
В изобарном процессе при сообщении газу массой m количества теплоты dQ=mCpdt /μ его внутренняя энергия возрастёт на величину dU = mCvdT /μ.
в) изотермический процесс (T = const).Изотермический процесс описывается законом Бойля-Мариотта: PV = const. Диаграмма этого процесса (изотерма) в координатах P, V представляет собой гиперболу. Работа изотермического расширения газа будет:
.
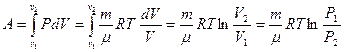Так как при T = const внутренняя энергия идеального газа не изменяется: dU = mCvdT /μ = 0, то следует, что для изотермического процесса dQ = dA, т.е. всё количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
.
Следовательно, для того чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
г) адиабатический процесс – это процесс, при котором отсутствует теплообмен (dQ = 0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Такой же процесс происходит в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д.
Из первого начала термодинамики для адиабатического процесса следует что dA = - dU, т.е. внешняя работа совершается за счёт изменения внутренней энергии системы. Для данного процесса можно записать, что
PV γ = const. – уравнение Пуассона.
Для перехода к переменным T,V или P,T исключим из уравнения с помощью
уравнения Менделеева – Клапейрона соответственно давление и объём, тогда:
TV γ-1 =const, T γ P 1-γ =const
тоже будут представлять уравнения адиабатического процесса. Диаграмма данного процесса в координатах P,V изображается гиперболой. Работа, совершаемая газом в адиабатическом процессе, записывается как
.