20. Элементы релятивистской динамики. Закон взаимодействия массы и энергии. Изменение массы тела со скоростью. Границы применимости классической механики.

Согласно представлениям классической механики масса тела есть величина постоянная. Однако в конце XIX столетия на опытах с быстро движущимися электронами было установлено, что масса тела возрастает с увеличением скорости по закону:  , (17)

где   - масса покоя.

Н а рис. 4 представлена зависимость   отV/c.

Релятивистский импульс

Он равен произведению релятивистской массы на скорость

. (18)

Основное уравнение релятивистской динамики имеет вид

 или  . (19)

В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса:

"релятивистский импульс замкнутой системы сохраняется".

Из этого закона следует закон сохранения релятивистской массы:

"полная релятивистская масса замкнутой системы сохраняется".

Закон взаимосвязи массы и энергии

Важным результатом теории относительности Эйнштейна является универсальное соотношение между энергией т ела и его массой

. (20)

Уравнение (20) выражает фундаментальный закон природы - закон взаимосвязи массы и энергии. В силу однородности времени в релятивистской механике, как и в классической, выполняется закон сохранения энергии:

"полная энергия замкнутой системы сохраняется".

Разложив (20) в ряд и пренебрегая членами второго порядка малости, получим

 (21)

Величина   (22)

называется энергией покоя.

В общем случае кинетическая энергия

.

Из формул (20) и (18) следует, что

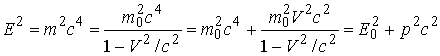, т.е.

. (23)

Анализируя уравнение (20), отметим, что оно имеет универсальный характер, применимо ко всем формам энергии и можно утверждать, что с энергией связана масса

т = Е/с² (24)

и, наоборот, со всякой массой связано определенное количество энергии (20). Закон взаимосвязи массы и энергии подтверждается при протекании ядерных реакций.

Изменение массы тела со скоростью

Второй закон Ньютона, выражающий связь силы, массы и ускорения - F = ma - может быть записан и через импульс:

F = ma = m(dv/dt) = d(mv)/dt = dP/dt,

где Р - это импульс - произведение массы на скорость. Такая запись второго закона Ньютона, где сила определяется как производная от импульса, называется дифференциальной записью.

При ускорении электрона под действием электромагнитного поля выяснилось, что при скоростях, близких к скорости света второй закон Ньютона в дифференциальной форме остается справедливым в том случае, если импульс записывать не как P = mv, а следующим образом:

P = mvγ = mv/√(1-v²/c²)

где γ - лоренцев множитель. Если определять импульс как произведение массы на скорость, то тогда получится, что масса тел зависит от их скорости:

m = m₀γ = m₀/√(1-v²/c²)

Где m₀ - это масса тела, когда его скорость равна нулю. Ее называют масса покоя. Согласно этой формуле теории относительности, когда тело неподвижно, его масса минимальна, при малых скоростях изменение массы практически незаметно, а при скоростях, приближающихся к скорости света, масса тел всё более растет, и при скорости, равной скорости света, получается бесконечно большая масса. Поэтому двигаться со скоростью света нельзя. Единственнным исключением является частица света - фотон. Он движется со скоростью света, поскольку его масса покоя равна нулю. Это значит, что фотон может существовать, только двигаясь со скоростью света. Если фотон остановить, то он исчезает, а его энергия поглощается.