8. 1. Поставим между точечным источником и точкой наблюдения непрозрачный экран с круглым отверстием.

Согласно Френелю, действие такого препятствия сходится к тому, что экран как-бы устраняет часть волнового фронта.

Будем предпологать, кроме того, что размеры отверстия можно менять, что дает возможность открывать любое число зон Френеля.

Если открыть первую зону Френеля, то амплитуда и интенсивность света в той же точке будут .

При удалении от центра интенсивность будет монотонно убывать. При расширении отверстия в точку начнут проходить вторичные волны. Их интерференция с ранее пришедшими волнами вызовет уменьшение интенсивности в той же точке. Когда отверстие откроет две первые зоны Френеля, то их действия в точке практически полностью уничтожат друг-друга из-за интерференции. В точке получиться темный кружок , окруженный светлым кольцом.

Вообще, при нечетном количестве открытых зон центр дифракционных колец светлый, при четном темный.

2 Определим теперь размеры и число зон Френеля, укладывающихся в отверствии . Пусть -диаметр отверствия, а и - расстояние от его центра до точек и . Из точек и как из центров опишем сферы, проходящие через край отверстия . Пренебрегая квадратами отрезков и , по известной теореме можно написать:

Отсюда

Число найдется делением этого отрезка на . Оно равно

Если целое, то будет диаметром, a - радиусом -ой, точнее ее внешнего края. Следовательно

9. Дифракция Фраунгофера (или дифракция плоских световых волн, или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию.

Д ля наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели ( ), - длина, b - ширина. Разность хода между лучами 1 и 2 в направ­лении φ

Разобьём волновую поверхность на участке щели МN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уложится   зон. Т.к. свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Число зон Френеля   укладывающихся на ширине щели, зависит от угла φ.

Условие минимума при дифракции Френеля:

Если число зон Френеля четное

или

то в т. Р наблюдается дифракционный минимум.

Условие максимума:

Если число зон Френеля нечетное

то наблюдается дифракционный максимум.

10. Дифракция света на дифракционной решетке

      Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками (рис. 9.6).

      Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

      Обозначим: b – ширина щели решетки; а – расстояние между щелями;  – постоянная дифракционной решетки.

      Линза собирает все лучи, падающие на нее под одним углом и не вносит никакой дополнительной разности хода.

Рис. 9.6	Рис. 9.7

      Пусть луч 1 падает на линзу под углом  φ (угол дифракции). Световая волна, идущая под этим углом от щели, создает в точке  максимум интенсивности. Второй луч, идущий от соседней щели под этим же углом φ, придет в ту же точку . Оба эти луча придут в фазе и будут усиливать друг друга, если оптическая разность хода будет равна mλ:

      Условие максимума для дифракционной решетки будет иметь вид:

,

(9.4.4)

      где m = ± 1, ± 2, ± 3, … .

      Максимумы, соответствующие этому условию, называются главными максимумами. Значение величины m, соответствующее тому или иному максимуму называется порядком дифракционного максимума.

      В точке F₀ всегда будет наблюдаться нулевой или центральный дифракционный максимум.

      Так как свет, падающий на экран, проходит только через щели в дифракционной решетке, то условие минимума для щели и будет условием главного дифракционного минимума для решетки:

.

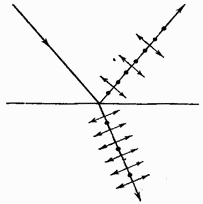
11. Если угол падения света на границу раздела двух диэлектриков (например, на поверхность стеклянной пластинки) отличен от нуля, отраженный и преломленный лучи оказываются частично поляризованными . В отраженном луче преобладают колебания, перпендикулярные к плоскости падения (на рис. 135.1 эти колебания обозначены точками), в преломленном луче — колебания, параллельные плоскости падения (на рисунке они изображены двусторонними стрелками). Степень поляризации зависит от угла падения.

Обозначим через угол, удовлетворяющий условию

 

( — показатель преломления второй среды относительно первой). При угле падения равном отраженный луч полностью поляризован (он содержит только колебания, перпендикулярные к плоскости падения). Степень поляризации преломленного луча при угле падения, равном достигает наибольшего значения, однако этот луч остается поляризованным только частично.

Соотношение (135.1) носит название закона Брюстера, а угол называют углом Брюстера. Легко убедиться в том, что при падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.

Степень поляризации отраженного и преломленного лучей при различных углах падения можно получить с помощью формул Френеля.

12. Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора.

где  — интенсивность падающего на поляризатор света,  — интенсивность света, выходящего из поляризатора,  — коэффициент пропускания поляризатора.

13.   Дисперсией света называется зависимость показателя преломления n вещества от частоты ν (длины волн λ) света или зависимость фазовой скорости  световых волн  от их частоты.

Классическая теория дисперсии, развитая Лоренцом для среды без поглощения, дает:

,

(4.1)

где - концентрация атомов среды, e, и m - заряд и масса электрона, - электрическая постоянная, - циклическая частота собственных колебаний электрона в атоме и - циклическая частота падающего излучения. Графическое изображение (4.1) дано на рисунке 4.1.

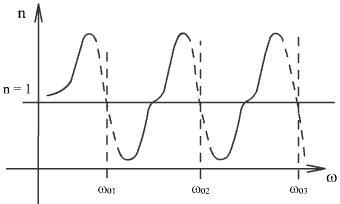Рис. 4.1 Дисперсионные спектры призм

При прохождении светового потока сквозь призму белый свет разлагается в многоцветный спектр, который называют призматическим, или дисперсионным спектром.

14. Теплово́е излуче́ние — электромагнитное излучение, возникающее за счёт внутренней энергии тела^[1]. Имеет сплошной спектр, максимум которого зависит от температуры тела. При остывании последний смещается в длинноволновую часть спектра.

Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:

Мощность излучения абсолютно чёрного тела прямо пропорциональна площади поверхности и четвёртой степени температуры тела:

где - степень черноты (для всех веществ , для абсолютно черного тела ). При помощи закона Планка для излучения, постоянную можно определить как

Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.

λ_max = b/T ≈ 0,002898 м·К × T ⁻¹ (K),

где T — температура, а λ_max — длина волны с максимальной интенсивностью. Коэффициент b, называемый постоянной Вина, в системе СИ имеет значение 0,002898 м·К.

Для частоты света (в герцах) закон смещения Вина имеет вид:

где

α ≈ 2,821439…  — постоянная величина (корень уравнения ),

k — постоянная Больцмана,

h — постоянная Планка,

T — температура (в кельвинах).