1.Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1] Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции 

 — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. 

Энергию магнитного поля в катушке индуктивности можно найти по формуле:

Зако́н Ампе́ра  — закон взаимодействия электрических токов. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Модуль силы Ампера можно найти по формуле:

2. Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q - заряд частицы; V - скорость заряда;  B - индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции.

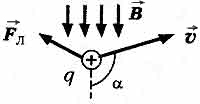
Направление силы Лоренца определяется по правилу левой руки:

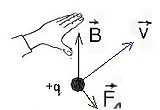
3. 1. Линии индукции направлены перпендикулярно скорости заряда:  B = const. Ускорение заряда:  ; так как вектор ускорения a, то ускорение является нормальным:  . Частица движется по окружности радиуса 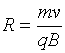 . Время одного оборота: 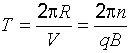 . Время Т не зависит от скорости.

2. Скорость v параллельна B. В этом случае sin(vB) = 0, F = qvBsin(vB) = 0,  . Частица движется равномерно и прямолинейно, вдоль вектора B.

Рассмотренные свойства движущихся в магнитном поле заряженных частиц находят широкое применение в технике. В 1932 г. Э.О. Лоуренс (Калифорнийский университет в Беркли) разработал циклотрон для ускорения заряженных элементарных частиц типа протонов и ионов. Использование ускоренных до высоких энергий частиц в качестве «снарядов» при изучении столкновений ядерных частиц позволило получить информацию об атомных ядрах и элементарных частицах. В 1879 г. был открыт так называемыйэффект Холла, суть которого заключается в следующем. Если проводник, по которому течет ток, жёстко закреплен в магнитном поле, это поле оказывает на заряды, движущиеся в проводнике, силовое воздействие, перпендикулярное их движению.

Если, например, электроны движутся в прямоугольном проводнике вправо, то магнитное поле, направленное перпендикулярно движению электронов, будет создавать силу, направленную вниз. В результате электроны будут двигаться вблизи нижней поверхности, поэтому между поверхностями возникнет разность потенциалов. Она будет увеличиваться до тех пор, пока обусловленное ею электрическое поле не уравновесит силу, действующую на движущиеся заряды со стороны магнитного поля. В большинстве случаев ток отрицательных зарядов вправо эквивалентен току положительных зарядов влево. Однако эффект Холла позволяет различать эти два случая. Движущиеся влево положительные заряды будут отклоняться вниз, так что нижняя поверхность приобретает положительный потенциал по отношению к верхней. Именно по полярности эдс Холла впервые удалось установить, что в проводниках носители имеют отрицательный заряд. Величина эдс Холла пропорциональна силе тока и магнитной индукции.  Поэтому эффект Холла может быть использован для измерения магнитных полей. Вначале проводник (датчик Холла) калибруется в известных магнитных полях. Если поддерживать силу тока в нем постоянной, то, измеряя эдс Холла, можно определить индукцию магнитного поля В. Датчики Холла очень удобны, они имеют малые размеры и обеспечивают высокую точность измерений.

4.Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).

.

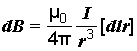
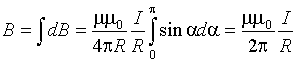
5. Индукция магнитного поля в произвольной т. А, созданного бесконечно длинным прямым проводником с током,

6. Магнитная индукция поля в центре кругового тока радиусом R

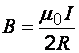
7.  В произвольной точке конечного соленоида магнитную индукцию можно найти по формуле

     Магнитная индукция поля внутри соленоида

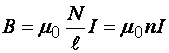
8. Два параллельных бесконечно длинных и тонких проводника с токами I₁ и I₂, расположенные на расстоянии а друг от друга, взаимодействуют с силой на единицу длины 

Это вытекает из закона Ампера. Причем, когда токи в проводниках параллельны, проводники притягиваются, а когда токи в проводниках антипараллельны - проводники отталкиваются.

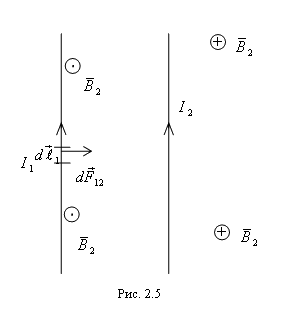Рис. 2.5

Рассмотрим задачу (рис. 2.5). Первый проводник находится во внешнем поле, созданном вторым проводником. Тогда 

или 

.

Направления   и   взаимно перпендикулярны и 

,

и, окончательно: 

или 

.

Пусть теперь второй проводник находится в поле, созданном первым проводником. Рассуждая по такой же схеме, получим: 

или 

,

.

9. Магни́тный пото́к — поток   как интеграл вектора магнитной индукции   через конечную поверхность  . Определяется через интеграл по поверхности

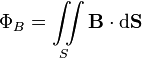
Тогда суммарный магнитный поток будет равен интегралу по площади S

10. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле   , перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор    сонаправлен с   .

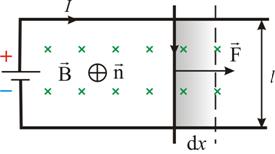
Рис. 2.17

      На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:

      Пусть проводник l переместится параллельно самому себе на расстояние  dx. При этом совершится работа:

      Итак,

      Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.

      Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.

11.   Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток   , пронизывающий контур, направлен по нормали    к контуру, поэтому   .

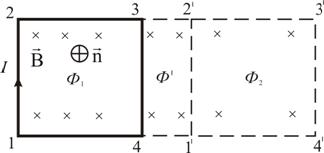
Рис. 2.18

      Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и  новый контур будет пронизан магнитным потоком   .

      Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком   .

      Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:

где   ,    равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).

 .

      Провод 1–2 перерезает поток (   ), но движется против сил действия магнитного поля.

 .

      Тогда общая работа по перемещению контура

  или

,

здесь    – это изменение магнитного потока, сцепленного с контуром.

      Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.

      Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле

,

12. Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы(ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле.Электрический ток, вызванный этой ЭДС, называется индукционным током.

Согласно закону электромагнитной индукции Фарадея (в СИ):

Знак «минус» в формуле отражает правило Ленца, Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

13. Вихревое электрическое поле  Перейдем в систему отсчета, связанную с подвижной стороной рамки.

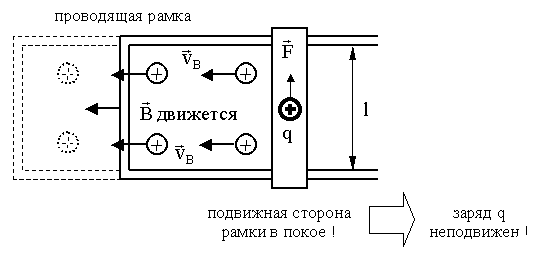
В этой системе отсчета v = 0,  , но магнитное поле движется со скоростью  .  Так как заряд q неподвижен и на неподвижный заряд q действует сила величиной  , значит, эта сила действует со стороны ЭЛЕКТРИЧЕСКОГО ПОЛЯ напряженностью (9.3.3.):

.

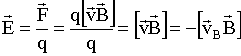Источником этого электрического поля является не заряд, как в статическом случае (9.3.1), а движущееся магнитное поле. Такое электрическое поле называют вихревым, т. к. его линии напряженности замкнуты. Работа вихревого поля по перемещению заряда по замкнутому контуру не равна нулю (в отличии от электростатического поля).

14. Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция)  , которая выражается в системе СИ в тесла [Тл], внутри катушки является фактически постоянной и (приближённо) равна

где   − магнитная постоянная,   − число витков,   − ток, записанный в амперах [А] и   − длина катушки в метрах [м]. Пренебрегая краевыми эффектами на концах соленоида, получим^[16], что потокосцепление через катушку равно плотности потока   [Тл], умноженному на площадь поперечного сечения   [м²] и число витков  :

Отсюда следует формула для индуктивности соленоида (без сердечника):

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель   — относительную магнитную проницаемость^[17] сердечника:

В случае, когда  , можно (следует) под S понимать площадь сечения сердечника [м²] и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

15. Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем больше часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощьютрансформатора.

 Самоиндукция  Контур с током I по (11.4) создает В ~ I, по (11.9.3) - магнитный поток Ф через контур пропорционален току I.

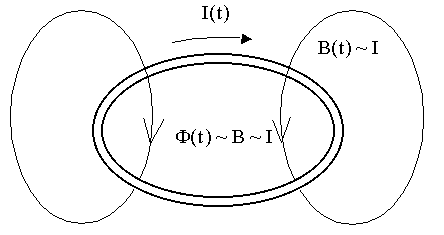
Можно записать связь между потоком и током:

,

здесь L - индуктивность контура, [L] = Гн (генри).  Если I ≠ const, I = I(t), то Ф = Ф(t), и возникает ЭДС индукции, по (11.10.1)

,

если L = const, то

.

16. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна    Значит, энергия магнитного поля, которое связано с контуром,   (1)  Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем    Так как I=Bl/(μ₀μN) и В=μ₀μH , то   (2)  где Sl = V — объем соленоида.  Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью   (3) 

17. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества. Опыт позывает, что все вещества, помещенные в магнитное поле, намагничиваются. Природа молекулярных токов стала понятной после того как опытами Резерфорда было установлено, что атомы всех веществ состоят из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов. Движение электронов в атомах подчиняется квантовым законам. Магнетизм вещества удается объяснить посредством модели Бора, согласно которой электроны в атомах движутся по стационарным круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом: P_m = ISn, модуль которого

 P_m = IS = eS, где I = e – сила тока;  – частота вращения электрона по орбите; S – площадь орбиты. Если электрон движется по часовой стрелке (рис. 5.1), то ток направлен против часовой стрелки и вектор P_m (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона.

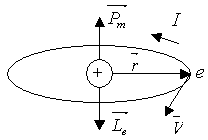
Рис. 5.1. Орбитальные магнитный момент P_m и механический момент L_e электрона

С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса L_e, модуль которого

L_e = mV = 2mS,                                                                                                    (5.2)

где V = 2r, r² = S. Вектор L_e (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона. Из рис. 5.1 следует, что направление P_m и L_e противоположны, поэтому, учитывая выражение (5.1) и (5.2), получим

 P_m  L_e = gL_e,                                                                                                (5.3)

 где величина

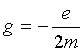                                                                                                          (5.4)

 называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком << - >>, указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения V и r различны. Формула (5.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.

18. Диамагне́тики — вещества, намагничивающиеся против направления внешнего магнитного поля. В отсутствие внешнего магнитного поля диамагнетики немагнитны. Под действием внешнего магнитного поля каждый атом диамагнетика приобретает магнитный момент I (а каждая единица объёма —намагниченность M), пропорциональный магнитной индукции B и направленный навстречу полю. Поэтому магнитная восприимчивость   = M/H у диамагнетиков всегда отрицательна. По абсолютной величине диамагнитная восприимчивость   мала и слабо зависит как от напряжённости магнитного поля, так и оттемпературы.

Другими словами, магнитная проницаемость   и слабо зависит как от напряжённости магнитного поля, так и от температуры.

Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля (J↑↑H) и имеют положительнуюмагнитную восприимчивость. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы  .

Термин «Парамагнетизм» ввёл в 1845 году Майкл Фарадей, который разделил все вещества (кроме ферромагнитных) на диа- и парамагнитные.

Атомы (молекулы или ионы) парамагнетика обладают собственными магнитными моментами, которые под действием внешних полей ориентируются по полю и тем самым создают результирующее поле, превышающее внешнее. Парамагнетики втягиваются в магнитное поле. В отсутствии внешнего магнитного поля парамагнетик не намагничен, так как из-за теплового движения собственные магнитные моменты атомов ориентированы совершенно беспорядочно.

Для количественного описания намагничивания магнитиков вводят векторную величину – намагниченность, определяемую магнитным моментом единицы объема магнетика:

 J = P_m /V = P_a /V,                                                                                                        (5.7)

 где P_m = P_a – магнитный момент магнетика, представляет собой векторную сумму магнитных моментов отдельных молекул [см. (5.6)].

Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда можем записать, что вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукции внешнего поля B₀ (поля, создаваемого намагничивающим током в вакууме) и поля микротоков B (поля, создаваемого молекулярными токами):

 B = B₀ + B ,                                                                                                            (5.8)

где B₀ = ₀H. Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поле с индукцией B₀. Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис. 5.3). Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.

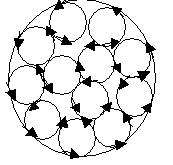
Рис. 5.3. Молекулярные токи

Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле, магнитную индукцию B которого можно вычислить, учитывая формулуB = NI/l для N = 1 (соленоид из одного витка):

 B´= I´/l,                                                                                                              (5.9)

 где I´ – сила молекулярного тока; l – длина рассматриваемого цилиндра, а магнитная проницаемость  принята равной единице. С другой стороны, I´/l – ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока: P = I´lS/l = I´V/l, где V – объем магнетика. Если P – магнитный момент магнетика объемом V, то намагниченность магнетика J

 J = P/V = I´/l.                                                                                                      (5.10)

 Сопоставляя (5.9) и (5.10), получим

B´= ₀J

или в векторной форме

 B´= ₀J.                                                                                                       (5.11)

Подставив выражение для B₀ и B в (5.11), получим

 B = ₀H + ₀J = ₀ (H + J).                                                                                   (5.12)

Как показывает опыт, в несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничивание, т. е.

 J = H,                                                                                                          (5.13)

где  – безразмерная величина, называемая магнитной восприимчивостью среды. Используя формулы (5.13) и (5.12), это выражение можно записать в виде

 B = ₀(1 + )H,                                                                                                    (5.14)

откуда

H = B /( ₀ (1 + )).

Безразмерная величина

  = ( 1+ )                                                                                                        (5.15)

 представляет собой магнитную проницаемость вещества. Подставив (5.15) в (5.14) придем к соотношению

 B = ₀H.                                                                                                       (5.16)

 Основными характеристиками магнитных свойств веществ являются магнитная восприимчивость  и магнитная проницаемость . Вещества с отрицательными значениями магнитной восприимчивости:  < 0 ( < 1) называют диамагнетиками. Вещества с небольшими, но положительными значениями магнитной восприимчивости:  > 0 ( > 1) называют парамагнетиками

19. Ферромагнетики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или моментов коллективизированных электронов (в металлических кристаллах). Иными словами, ферромагнетик — такое вещество, которое при температуре ниже точки Кюри, способно обладать намагниченностью в отсутствие внешнего магнитного поля.

Домен — макроскопическая область в магнитном кристалле, в которой ориентация вектора спонтанной однородной намагниченности^[1] или вектора антиферромагнетизма^[2] (при температуре ниже точки Кюри или Нееля соответственно) определенным образом повернута или сдвинута относительно направлений соответствующего вектора в соседних доменах. Домены существуют в ферро- и антиферромагнитных, сегнетоэлектрических кристаллах и других веществах, обладающих спонтанным дальним порядком. Точка Кюри, или температура Кюри, — температура фазового перехода II рода, связанного со скачкообразным изменением свойств симметрии вещества (например, магнитной — в ферромагнетиках, электрической — в сегнетоэлектриках, кристаллохимической — в упорядоченных сплавах). Названа по имени П. Кюри^[1]. При температуре   ниже точки Кюри   ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью и определённой магнитно-кристаллической симметрией. В точке Кюри ( ) интенсивность теплового движения атомов ферромагнетика оказывается достаточной для разрушения его самопроизвольной намагниченности («магнитного порядка») и изменения симметрии, в результате ферромагнетик становится парамагнетиком. Аналогично уантиферромагнетиков при   (в так называемой антиферромагнитной точке Кюри или точке Нееля) происходит разрушение характерной для них магнитной структуры (магнитных подрешёток), и антиферромагнетики становятся парамагнетиками. В сегнетоэлектриках и антисегнетоэлектриках при  тепловое движение атомов сводит к нулю самопроизвольную упорядоченную ориентацию электрических диполей элементарных ячеек кристаллической решётки. В упорядоченных сплавах в точке Кюри (её называют в случае сплавов также точкой Курнакова) степень дальнего порядка в расположении атомов (ионов) компонентов сплава становится равной нулю. Магнитный гистерезис — явление зависимости вектора намагничивания и вектора напряженности магнитного поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках — Fe, Co, Ni и сплавах на их основе. Именно магнитным гистерезисом объясняется существование постоянных магнитов.

Явление магнитного гистерезиса наблюдается не только при изменении поля H по величине и знаку, но также и при его вращении (гистерезис магнитного вращения), что соответствует отставанию (задержке) в изменении направления M с изменением направления H. Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H.

Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания. Эти изменения обусловлены смещением доменных границ и ростом одних доменов за счёт других, а также вращением вектора намагниченности в доменах под действием внешнего магнитного поля. Всё, что задерживает эти процессы и способствует попаданию магнетиков в метастабильные состояния, может служить причиной магнитного гистерезиса.

В однодоменных ферромагнитных частицах (в частицах малых размеров, в которых образование доменов энергетически невыгодно) могут идти только процессы вращения M. Этим процессам препятствует магнитная анизотропия различного происхождения (анизотропия самого кристалла, анизотропия формы частиц и анизотропия упругих напряжений). Благодаря анизотропии, M как-будто удерживается некоторым внутренним полем   (эффективным полем магнитной анизотропии) вдоль одной из осей лёгкого намагничивания, соответствующей минимуму энергии. Магнитный гистерезис возникает из-за того, что два направления M(по и против) этой оси в магнитоодноосном образце или несколько эквивалентных (по энергии) направлений М в магнитомногоосном образце соответствуют состояниям, отделённым друг от друга потенциальным барьером (пропорциональным  ). При перемагничивании однодоменных частиц вектор M рядом последовательных необратимых скачков поворачивается в направлении H. Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M коэрцитивная сила  . Более универсальным является механизм неоднородного вращения M. Однако наибольшее влияние на   он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом   может быть существенно меньше эффективного поля анизотропии формы. Сегнетоэлектрический гистерезис — неоднозначная петлеобразная зависимость поляризации P сегнетоэлектриков от внешнего электрического поля E при его циклическом изменении. Сегнетоэлектрические кристаллы обладают в определенном температурном интервале спонтанной (самопроизвольной, то есть возникающей в отсутствие внешнего электрического поля) электрической поляризацией P_c. Направление поляризации может быть изменено электрическим полем. При этом зависимость P(E) в полярной фазе неоднозначна, значение P при данном E зависит от предыстории, то есть от того, каким было электрическое поле в предшествующие моменты времени. Основные параметры сегнетоэлектрического гистерезиса:

• остаточная поляризация кристалла P_ост, при E = 0

• значение поля E_Kt(коэрцитивное поле) при котором происходит переполяризация

20. Получим закон изменения тока и напряжения для идеального контура. Поскольку в колебательном контуре конденсатор подключен параллельно катушке индуктивности, то напряжение на конденсаторе   должно равняться ЭДС самоиндукции   и по законам электродинамики

                                             ,                                                (3.6)

где q – заряд на обкладке конденсатора. Учтем, что по определению сила тока

                                                       .                                                                 (3.7)

Подстановкой силы тока в равенство (3.6) после простых преобразований получим

                                             ,                                                                    (3.8)

где                                                                                            (3.9)

называется циклической частотой колебаний. Здесь T – период колебаний, а   – частота колебаний или число колебаний в единицу времени.

    Уравнение (3.8) называется дифференциальным уравнением колебаний, в котором зависимость заряда от времени явно не видна. Получение такой зависимости принято называть решением дифференциального уравнения. Подстановкой в него можно убедиться что решением является зависимость заряда от времени

                                             ,                                                        (3.10)

где   – амплитуда заряда;  – начальная фаза колебания. Данное уравнение описывает гармоническое колебание заряда в колебательном контуре, а циклическая частота этих колебаний   носит название собственной частоты колебательного контура.

    Подставив уравнение (3.10) в формулы (3.6) и (3.7), получим законы изменения напряжения

                                                                                                            (3.11)

с амплитудой   и тока

                                         ,                          (3.12)

с амплитудой  . Таким образом, напряжение и ток в колебательном контуре изменяются по гармоническому закону.

21-22. В реальном контуре имеют место следующие потери энергии:

1) тепловые потери, так как  ;

2) потери в диэлектрике конденсатора;

3) гистерезисные потери в сердечнике катушки;

4) потери на излучение и др.

Уравнение колебаний можно получить, исходя из того, что сумма падений напряжения на ёмкости, индуктивности и активном сопротивлении должна быть равна нулю:

  .                                                                                                      (8.7)

Разделив это выражение на L и заменив I через  , а   через  , получим

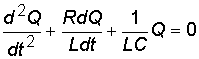  .                                                                                                 (8.8)

Беря во внимание, что   равно квадрату собственной частоты контура ₀, вводим обозначение:  , после этого уравнение принимает вид

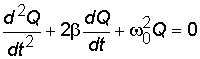  .                                                                                                 (8.9)

При условии, что  , т. е. 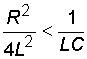 , уравнения имеет вид

  ,                                                                                             (8.10)

где  . Подставив значение для ₀ и для , находим :

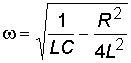  .                                                                                                         (8.11)

Таким образом, частота затухающих колебаний меньше собственной частоты ₀. Разделив выражение (8.10) на емкость С, получим напряжение на конденсаторе:

  .                                                                            (8.11)

 Амплитуда затухающих колебаний изменяется по закону  , где А₀ – начальная амплитуда. Зависимость амплитуды показана на рис. 8.3.

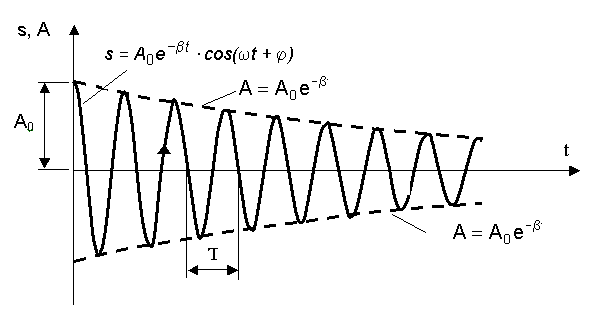
Рис. 8.3. График затухающих колебаний

Промежуток времени  , в течение которого амплитуда уменьшается в e раз, называется временем релаксации. Если А(t) и А(t + Т) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

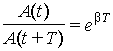                                                                                                         (8.12)

называется декрементом затухания, а его логарифм –

                                                                                               (8.13)

логарифмическим декрементом затухания; N – число колебаний, совершаемых за время уменьшения амплитуды в e раз. Для характеристики колебательной системы пользуются понятием добротности, которая при малых значениях логарифмического декремента равна:

  .    

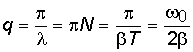23. Если рассматривать колебательный контур, то для получения вынужденных колебаний (рис. 8.4), нужно включить последовательно с элементами контура переменную эдс или, разорвав контур, подать напряжение:

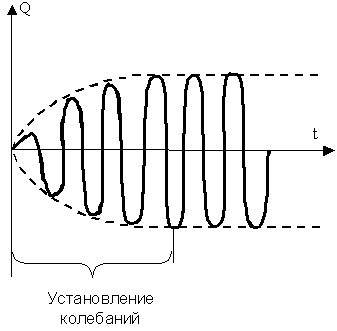
Рис. 8.4. Вынужденные колебания в колебательном контуре

U = U_mcos, тогда уравнение будет иметь вид:

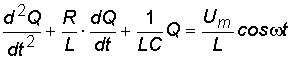  ,                                                                                                           (8.15)

 

после замены получим

  .                                                                                     (8.16)

Решение полученного неоднородного дифференциального уравнения находим прибавлением к его частному решению общего решения соответствующего однородного уравнения. Частное решение имеет вид

,

где  .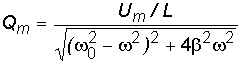

Подставив в эти выражения значения  , получим:

  .                                                                                            (8.17)

 Разделив заряд на емкость, получим напряжение на конденсаторе:

,

где 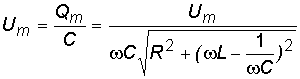 . Установившийся ток в контуре  . Амплитуда тока имеет вид

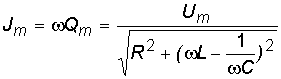  .                                                                                     (8.18)

 

Резонансная частота для контура

  .                                                                           (8.19)

Резонансные кривые для U_C и тока I имеют такой вид, как показано на рис. 8.5.

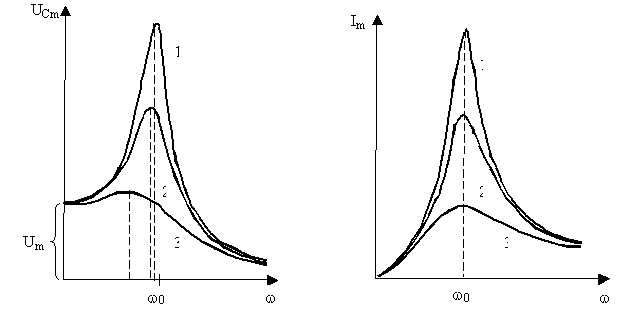
Рис. 8.5. Явление резонанса напряжений и токов в колебательном контуре: кривые 1, 2, 3 соответствуют всё бóльшему активному сопротивлению контура

 

При   резонансные кривые стремятся к U_m – напряжению, возникающему на конденсаторе при подключению его к источнику постоянного напряжения. Максимум при резонансе получается тем выше и острее, чем меньше  , т. е. чем меньше активное сопротивление и больше индуктивность контура. Тогда амплитуда силы тока имеет максимальное значение при  . Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура  .

Мы рассмотрели вынужденные колебания, возникающие при включении внешнего напряжения последовательно с элементами колебательного контура. Явление резонанса используется для выделения из сложного напряжения нужной составляющей, настроив контур на одну из частот   и т. д. (т. е., подобрав соответствующим образом его параметры С и L, можно получить на конденсаторе напряжение, в несколько раз превышающее величину данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляющими, будет слабым. Такой процесс имеет место, например, при настройке радиоприемника на нужную длину волны.

24. Ток смещения или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

Введение тока смещения позволило устранить противоречие^[1] в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.

Строго говоря, ток смещения не является^[2] электрическим током, но измеряется в тех же единицах, что и электрический ток.

В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения   (с точностью до универсального постоянного коэффициента) называется^[3] поток вектора быстроты изменения электрического поля   через некоторую поверхность^[4]  :

25. Электромагни́тное по́ле — фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, а также с телами, имеющими собственные дипольные и мультипольные электрические и магнитные моменты. Представляет собой совокупность электрического и магнитного полей, которые могут, при определённых условиях, порождать друг друга, а по сути являются одной сущностью, формализуемой через тензор электромагнитного поля.

Электромагнитное поле (и его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это ещё одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.

В современной формулировке электромагнитное поле представлено тензором электромагнитного поля, компонентами которого являются три компонентанапряжённости электрического поля и три компонента напряжённости магнитного поля (или — магнитной индукции)^{[~ 1]}, а также четырёхмерным электромагнитным потенциалом — в определённом отношении ещё более важным.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированныеДжеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служитьспециальная теория относительности). Используя Гаусса- Остроградского формулу и С такса формулу, ур-ниям (1) - (4) можно придать формуинтегральных:

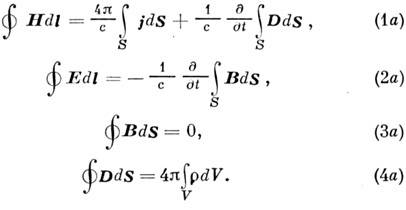
26. Особенности электромагнитных волн:

• наличие трёх взаимноперпендикулярных векторов: волнового вектора, вектора напряжённости электрического поля E и вектора напряжённости магнитного поля H.

Волновые свойства Править

Электромагнитные волны — это поперечные волны (волны сдвига), в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны.

Квантовые свойства Править

Квантовые свойства излучения проявляются при взаимодействии излучения с веществом — в частности, испускание и поглощение излучения происходит дискретными порциями.

Энергия кванта электромагнитного излучения определяется выражением:

     где   = 6,63×10⁻³⁴ Дж·с (постоянная Планка),   — частота волны.

Полезно заметить, что для длины волны   = 1000 нм энергия соответствующего кванта составляет 1,24 эВ, то есть приблизительно один электрон-вольт. На красном конце видимого спектра формула даёт 1,6 эВ, на фиолетовом — 3 эВ

Для фиксированного момента времени t₁ векторы  и  плоской гармонической электромагнитной волны могут быть изображены следующей диаграммой:

27. Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях.

В курсе электричества и магнетизма было показано, что объемная плотность энергии электрического поля равна

а магнитного поля –

где   и   – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна

Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением  , то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля:

Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры».

Плотность энергии электромагнитного поля можно представить в виде:

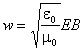
Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства.

Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку пройдет энергия  , равная

,

где   – скорость электромагнитной волны в вакууме.

Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:

Подставляя в последнее соотношение выражения для   и  , получим

.

Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

 (в системе СГС),

 (в СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответственно.

2. Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

      Итак, необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны – неограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Спектр частот реальной волны имеет конечную ширину . Если в какой-то момент времени волны были в фазе, через некоторое время  разность фаз будет уже равна π (волны в противофазе). Такую волну можно приближенно считать монохроматической только в течение времени

,

4. интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при , где  — длина волны. Если  нм, то толщина плёнки равняется 550:4=137,5 нм.

учи соседних участков спектра по обе стороны от  нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей

 — условие максимума;

 — условие минимума,

где k=0,1,2… и  — оптическая длина пути первого и второго луча, соответственно.

Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.

5. Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Кольца Ньютона. Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами^[2].