Вопросы для закрепления теоретического материала к практической работе.
Укажите необходимые и достаточные признаки максимума и минимума функций.
В каких случаях функция не имеет ни максимума, ни минимума?
Какие точки графика называют точками перегиба?
Сформулируйте правила исследования функций на точки перегиба.
Что необходимо знать для построения графика функции?
Инструкция по выполнению практической работы.
На выполнение практической работы дается 1 час 30 мин.(90 мин.). Работа состоит из 10 заданий. При их выполнении надо записать обоснованное решение. За выполнение работы выставляется оценка.
Методика анализа результатов, полученных в ходе практической работы.
Оценка тестовых заданий производится в соответствии с утвержденными критериями:
№ |
Процент правильных ответов |
Оценка по общепринятой шкале |
1 |
85-100 % |
Отлично |
2 |
70 – 84 % |
Хорошо |
3 |
50 – 69 % |
Удовлетворительно |
4 |
0 – 49 % |
Неудовлетворительно |
|
|
|
Порядок выполнения отчета по практической работе
Прочитать методические указания.
Решить определенный вариант.
Ответить на контрольные вопросы.
Вариант I
Найдите промежутки монотонности следующих функций:
а) f(x)=x2-6x+5; б) f(x)=2x2-4x+5;
в)
f(x)=
-
;
г)
y=lnx2;
д)
y=
2.
2. Исследуйте на экстремум следующие функции:
а) f(x)=x2-x; б) f(x)=x2-8x+12;
в)
f(x)=
x3-
4x.
Найти точки перегиба:
а)
(x)=x³-x;
б) y= x³-x²+8x-4
Вариант II
1.Найдите промежутки монотонности следующих функций:
а)
f(x)=-x2+4x+1;
б) f(x)=
-
x4-x+1;
в)
f(x)=
-2x3+15x2-36x+20;
г) y=
x2-lnx;
д)
y=
.
2.Исследуйте на экстремум следующие функции:
а) f(x)=x2+3x; б) f(x)=x2-4x+3;
в) f(x)= - x4+8x.
Найти точки перегиба:
𝑓 (x)=
-10x³+36x²-100;𝑓 (x)= -8x³+18x²-48x+31;
Вариант III
1.Найдите промежутки монотонности следующих функций:
а) f(x)=x3-3x2+1; б) f(x)==2x3-9x+12x-15;
в)
f(x)=
.;
г) y=e-x;
д) y=ln .².
2.Исследуйте на экстремум следующие функции:
а) f(x) = -x2+2x; б) f(x)=-x2+2x+3;
в) f(x)=2x3+9x2+12x-2.
3.Найти точки перегиба:
a) 𝑓 (x)= -6x³+12x²-10;
b)
𝑓
(x)=x
Вариант IV
1.Найдите промежутки монотонности следующих функций:
а)
f(x)=--
x3+
x2+2
; б) y=ln
x
x3;
в) f(x)=-x2-x; г) y=ex2;
д) f(x)= -2x2+x+1.
2.Исследуйте на экстремум следующие функции:
а)
f(x)=
23-3x2-12x+8;
б) f(x)
x3
–x2.;
в) f(x)= -x2-x+6. 3.
3.Найти точки перегиба:
a)
𝑓
(x)=
;
b)
𝑓
(x) =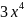
-2x³+6x²-5;
Вариант V
1.Найдите промежутки монотонности следующих функций:
а) f(x) = x4-4x+3; б) f(x)=4x4-32x+40;
в) f(x)= -2x2-3x+6; г) y=2ex2;
д) y=e1/x
2.Исследуйте на экстремум следующие функции:
а) f(x)=x2-10x+9; б) f(x)=2x4-x;
в) f(x)=2x3-9x2+12x-8.
3.Найдите точки перегиба:
a)
𝑓
(x) =
;
b)
𝑓
(x) =
-4x³+8x²-10;
Вариант I
Исследуйте функции и постройте их графики:
1)
y
=
2)
y
=
Вариант II
Исследуйте функции и постройте их графики:
1)
y
=
2)
y
=
Вариант III
Исследуйте функции и постройте их графики:
1
) y
=
2) y
=
Вариант IV
Исследуйте функции и постройте их графики:
1)
y
=
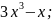2) y
=
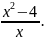
Вариант V
Исследуйте функции и постройте их графики:
1)
y
=
2)
y
=
