Вопросы для закрепления теоретического материала к практической работе.
Какое уравнение называется дифференциальным?
Что такое решение дифференциального уравнения?
Каких порядков бывают дифференциальные уравнения?
Какие решения уравнений вы знаете?
Инструкция по выполнению практической работы.
На выполнение практической работы дается 1 час 30 мин.(90 мин.). Работа состоит из 4 заданий. При их выполнении надо записать обоснованное решение. За выполнение работы выставляется оценка.
Методика анализа результатов, полученных в ходе практической работы.
Оценка тестовых заданий производится в соответствии с утвержденными критериями:
№ |
Процент правильных ответов |
Оценка по общепринятой шкале |
1 |
85-100 % |
Отлично |
2 |
70 – 84 % |
Хорошо |
3 |
50 – 69 % |
Удовлетворительно |
4 |
0 – 49 % |
Неудовлетворительно |
|
|
|
Порядок выполнения отчета по практической работе
Прочитать методические указания.
Решить определенный вариант.
Ответить на контрольные вопросы.
Вариант I
1)Найдите общие решения уравнений:
а)
(1=y²)dx-
б)
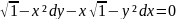
2)Найдите частные решения уравнений, удовлетворяющие указанным
начальным условием:
а)
= ctg
x
sin
y
dy;
y
при x
=
б) xdy = ydx; y = 6 при x = 2
Вариант 2
1) Найдите общие решения уравнений:
а)
x²dx
= 3y²dy;
б)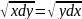
2) Найдите частные решения уравнений, удовлетворяющие указанным
начальным условием:
а) ydy = xdx; y = 4 при x = -2; 2 б) xdy = ydx; y = 6 при x = 2
Вариант 3
1) Найдите общие решения уравнений:
а)
=
;
б) (1+y)dx
= (x-1)dy
2) Найдите частные решения уравнений, удовлетворяющие указанным
начальным условием:
а)
ds
= (3t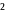
-2t)
dt;
s
= 4 при t
= 2; б)
=
;
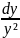y
= 2 при x
=0
Вариант 4
1) Найдите общие решения уравнений:
а) xy dx = (1+x²) dy; б) y²dx=(x-2)dy = 0
2) Найдите частные решения уравнений, удовлетворяющие указанным
начальным условием:
а)
=
;
y
= 4 при x
= 0 б) (1+y)dx
= (1-x)
dy;
y=3
при x
= -2
Вариант 5
1) Найдите общие решения уравнений:
а) (x²-yx²)dy+(y²+xy²)dx = 0; б) x²dy-(2xy+3y)dx = 0
2) Найдите частные решения уравнений, удовлетворяющие указанным
начальным условием:
а) = ; y = 2 при x =0 б) = ; y = 4 при x = 0