1 .Построение кривых свободной поверхности

.

i₀<i_к , h₀>h_кр.

РИСУНОК (лекции прошлый год)

- h>h₀ и k>k₀, => числитель > 0, и П_к<1 – знаменатель >0. => - функция возрастает – глубина возрастает вниз по течению – кривая подпора а₁.

- h<h₀ и h>h_кр, k<k₀, => числитель <0, и П_к<1 – знаменатель >0, => - глубина потока уменьшается вниз по течению – выпуклая кривая спада b₁.

- h<h_кр, h<h₀, k<k₀, П_к>1 –числитель и знаменатель <0, => - глубина потока возрастает вниз по течению – вогнутая кривая подпора с₁.

i₀>i_к. h₀<h_кр

РИСУНОК (лекции прошлый год)

- h>h_кр, h>h₀ и k>k₀, П_к<1 – числитель и знаменатель <0, => - происходит подпор – кривая подпора а₂.

- h>h_0, h<h_кр, k>k₀, П_к>1 – числитель >0, знаменатель <0, => - глубина уменьшается вниз по течению – кривая спада b₂.

- h<h₀, k<k₀, П_к>1 – числитель и знаменатель <0, => - глубина потока возрастает вниз по течению – кривая подпора с₂.

i₀=i_{к ,}h₀=h_кр.

РИСУНОК(лекции прошлый год)

- h>h₀ и k>k₀, П_к<1 – числитель и знаменатель >0 , => - глубина возрастает вниз по течению - прямая а₃.

- h<h_кр, k<k₀, П_к>1, => - кривая подпора, с₃ –прямая.

2.Типы задач на неравномерное движение.

Первый тип: известны глубины h₁ и h₂, требуется определить расстояние l между этими сечениями. В зависимости от уклона дна потока l определяется по формулам:

При прямом уклоне: ,

При нулевом уклоне: ,

При обратном уклоне: . Для определяем , , , , , .

Второй тип: известна глубина в одном из сечений (2-2), задано расстояние l между сечениями, необходимо определить глубину в сечении 1-1. решение методом последовательных приближений. Преобразуем: . Задаваясь произвольными h₁, определяем левую часть уравнения. Далее задаваясь величиной η₁, определяем φ(η₁), подставляем в правую часть, пока уравнение не превратится в тождество. -> h₁= η₁h₀ – первое приближение.

3.Определение длины кривой свободной поверхности потока при неравномерном движении по уравнению Бахметева.

Для русла с положительным уклоном дна: , где . После преобразования : , где . Выразим коэффициент Шези по формуле Маннинга, тогда: . Для широких и неглубоких русел В=Х, R=h. . При этом дифференциальное уравнение примет вид: . После ряда последовательного разделения переменных и интегрирования, получим: .

Для дна с горизонтальным руслом дна: равномерного движения не может быть, поэтому нормальная глубина отсутствует. После интегрирования получим: .

4.Уравнение Чарномского. Расчет кривых в естественных руслах.

РИСУНОК (стр. 237, Константинов)

Составим уравнение Бернулли для сечений 1—1 и 2—2 относительно

выбранной плоскости сравнения О2—О2,: Э+i₀Δl=Э+Δ hf. После приведения: i₀Δl = ΔЭ + Δh_f.

На участке между сечениями 1—1 и 2—2 движение жид­кости является плавноизменяющимся, поэтому энергия потока расходуется на преодоление сопротивлений по дли­не, а потери энергии на местные сопротивления можно счи­тать пренебрежимо малыми, т. е. Δhf=Δht. Отношение потерь напора к длине участка является средним значением гидравлического уклона на участке:

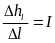, тогда или .

Для непризматических русл с уклонами дна i₀=O и i₀<0 уравнение и

Уравнения записаны в конечных разностях. В такой форме они впервые были приведены В. И. Чарномским.

При бесконечно малом расстоянии dl между сечениями 1—1 и 2—2 можно получить урав­нения в дифференциальной форме: , ,
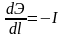