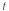5.3.3 Разложение булевой функции по переменным

Одной из задач булевой алгебры является задача представить произвольную булеву функцию, в том числе заданную таблично, используя только переменные, их отрицания, булевы суммы и булевы произведения. Для того, чтобы доказать такую возможность, сделаем предварительно несколько замечаний.

Определим . Из этого определения следует, что . Легко заметить, что тогда и только тогда, когда ; в противном случае .

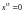Определение. Элементарной конъюнкцией (минитермом) переменных называется выражение , где равно 0 или 1. Выражение, представляющее собой булеву сумму элементарных конъюнкций, называется дизъюнктивной нормальной формой (суммой произведений), так что, если есть элементарные конъюнкции, то – дизъюнктивная нормальная форма. Запись может иметь вид или .

Лемма. Пусть – произвольный фиксированный набор значений переменных . Тогда, если хотя бы одно значение равно нулю, то и булево произведение равно нулю.

Это утверждение следует из закона ассоциативности и закона доминирования.

Лемма. Пусть – произвольный фиксированный набор значений переменных . Тогда, если хотя бы для одного значения верно, что , то выражение равно нулю.

Для доказательства используем предыдущую лемму и сделанное в начале параграфа наблюдение.

Лемма. Пусть есть элементарные конъюнкции и одна из них принимает значение единица на фиксированном наборе . Тогда дизъюнктивная нормальная форма равна единице на этом наборе.

Доказательство следует из закона доминирования для булевой суммы.

Теорема. Любая ненулевая булева функция может быть представлена в виде совершенной дизъюнктивной нормальной формы (СДНФ)

,

где суммирование происходит по тем и только тем наборам , на которых функция принимает значения, равные единице.

Доказательство. Зафиксируем произвольный набор . Докажем, что для этого набора значения в левой и правой части равенства одинаковы.

Пусть (значение в левой части равенства). В правой части равенства имеем . Поскольку суммирование ведётся по всем наборам, на которых функция принимает значения, равные единице, то для одного из них будет выполняться . Для этого набора . В силу последней из лемм и вся булева сумма, стоящая в правой части равна единице. Следовательно, если , то равенство выполняется.

Пусть (значение в левой части равенства). В левой части равенства имеем . Поскольку суммирование ведётся только по тем наборам, на которых функция принимает значения, равные единице, то любой из них будет отличаться от хотя бы по одной позиции. Это означает, что существует номер , для которого . В силу второй из лемм равно нулю. Поскольку булева сумма нулей равна нулю, то и значение в правой части равенства равна нулю, что соответствует значению в левой части.

В силу произвольности набора равенство справедливо для всех значений переменных , что и доказывает теорему.

Следствие 1. Любая булева функция может быть выражена через отрицание, булеву сумму и булево произведение.

Если функция отлична от тождественного нуля, то её можно представить, как показано выше, в виде СДНФ. Тождественный ноль можно выразить как .

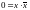Следствие 2. Любая булева функция может быть выражена через отрицание и булеву сумму.

Выразим булеву функцию через отрицание, сумму и произведение, а затем, используя закон де Моргана и закон двойного отрицания, выразим произведение через отрицание и сумму и применим это соотношение ко всем конъюнкциям (более того, по индукции можно доказать свойство , так что выражение измениться не сильно).

Аналогично можно доказать и следующее следствие.

Следствие 3. Любая булева функция может быть выражена через отрицание и булево произведение.

Пример. Найти СДНФ функции, заданной таблично

0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

Так как равны единице 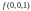, , , то, в соответствии с теоремой

или, используя определение ,

.

Возможно также, используя принцип двойственности, представить булеву функцию в виде совершенной конъюнктивной нормальной формы (СКНФ)

.
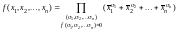