
- •Глава 5. Элементы дискретной математики
- •5.1.2 Операции над множествами
- •5.1.3 Представление множеств в компьютере
- •5.2.2 Свойства отношений
- •5.2.3 Операции над отношениями
- •5.2.5 Отношение эквивалентности
- •5.2.6 Отношение частичного порядка
- •5.3.3 Разложение булевой функции по переменным
- •5.3.4 Минимизация дизъюнктивных нормальных форм
- •5.3.5 Функциональная полнота
5.2.5 Отношение эквивалентности
Определение. Отношение на множестве есть отношение эквивалентности, если это отношение рефлексивно, симметрично и транзитивно.
Из рассмотренных в параграфе 5.2.1 отношений отношениями эквивалентности являются отношение равенства квадратов чисел и отношение «быть однофамильцем».
Ещё одним примером отношения эквивалентности является следующее отношение.
Определение. Пусть
─ множество целых чисел. Определим
отношение
 как множество пар чисел
как множество пар чисел
 таких, что
таких, что
 где
где
 ─ натуральное число, большее единицы,
─ натуральное число, большее единицы,
 ─ целое. В этом случае числа
и
называются сравнимыми
по модулю
(
─ целое. В этом случае числа
и
называются сравнимыми
по модулю
(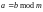 ).
Например,
).
Например,
 так как
так как

Покажем, что отношение сравнения по модулю является отношением эквивалентности.
Так как
 то отношение сравнения по модулю является
рефлексивным.
то отношение сравнения по модулю является
рефлексивным.
Если
 то
то
 и наоборот, что доказывает симметричность
отношения.
и наоборот, что доказывает симметричность
отношения.
Если
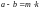 и
и
 то
то
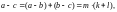 что свидетельствует о транзитивности
этого отношения.
что свидетельствует о транзитивности
этого отношения.
Поскольку доказано,
что отношение
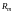 является рефлексивным, симметричным и
транзитивным, то оно является отношением
эквивалентности.
является рефлексивным, симметричным и
транзитивным, то оно является отношением
эквивалентности.
Пусть на множестве
определено отношение эквивалентности
 Возьмём произвольный элемент
Возьмём произвольный элемент
 принадлежащий множеству
принадлежащий множеству

Определение. Классом
эквивалентности элемента
по отношению эквивалентности
(обозначается
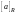 )
называется множество
)
называется множество

Пример. Рассмотрим
введённое выше отношение сравнения по
модулю
Положим
 Тогда всё множество целых чисел можно
разбить на три не пересекающих класса
эквивалентности:
Тогда всё множество целых чисел можно
разбить на три не пересекающих класса
эквивалентности:



Элементы класса
 похожи в том смысле, что каждый из них
кратен трём. Элементы любого другого
класса также похожи в том смысле, что
имеют один и тот же остаток при делении
на три.
похожи в том смысле, что каждый из них
кратен трём. Элементы любого другого
класса также похожи в том смысле, что
имеют один и тот же остаток при делении
на три.
Как видно из
приведённого выше примера, совокупность
классов эквивалентности разделяет всё
множество целых чисел
 на непустые не пересекающиеся подмножества.
Докажем следующее утверждение.
на непустые не пересекающиеся подмножества.
Докажем следующее утверждение.
Теорема. Пусть
─ отношение эквивалентности на множестве
Тогда для двух произвольных элементов
и
справедливо, что или
 или
или

Доказательство.
Пусть
 Тогда существует элемент
такой, что
Тогда существует элемент
такой, что
 и
и
 ,
то есть
,
то есть
 и
и
 Поскольку
─ отношение эквивалентности, то
─ симметричное отношение и, следовательно,
Поскольку
─ отношение эквивалентности, то
─ симметричное отношение и, следовательно,
 Так как
и
Так как
и
 то,
в силу транзитивности,
то,
в силу транзитивности,

Возьмём произвольный
элемент
 Тогда
Тогда

 поэтому
поэтому
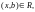 то
есть
то
есть
 В силу
произвольности
имеем включение
В силу
произвольности
имеем включение

Аналогично доказывается
и включение

Следовательно, верно
утверждение
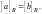
Пусть
─ отношение эквивалентности на множестве
В силу
рефлексивности
любой элемент
множества
принадлежит классу эквивалентности
и поэтому из равенства
 следует, что объединение всех классов
эквивалентности по отношению
даёт всё множество
следует, что объединение всех классов
эквивалентности по отношению
даёт всё множество
 то есть
то есть

Кроме того, из доказанной теоремы следует, что различные классы эквивалентности либо равны, либо не пересекаются, так что множество разбивается на не пересекающиеся подмножества.
Определение. Множество
 где
где
 – непустые подмножества
называется разбиением множества
если выполнена два условия:
– непустые подмножества
называется разбиением множества
если выполнена два условия:
а)
 для всех
для всех
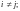
б)

Мы видим, что заданное на исходном множестве отношение эквивалентности формирует разбиение множества . Подмножествами такого разбиения являются соответствующие классы эквивалентности. И наоборот, каждое разбиение множества можно использовать для того, чтобы сформировать отношение эквивалентности: два элемента будут эквивалентными, если они принадлежат одному и тому же подмножеству разбиения.
Для того, чтобы
обосновать это, предположим, что
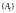 – разбиение множества
Пусть отношение
состоит из всех пар
– разбиение множества
Пусть отношение
состоит из всех пар
 таких, что
и
таких, что
и
 принадлежат одному и тому же подмножеству
разбиения. Для того, чтобы убедиться в
том, что
отношение эквивалентности, требуется
доказать, что оно рефлексивно, симметрично
и транзитивно.
принадлежат одному и тому же подмножеству
разбиения. Для того, чтобы убедиться в
том, что
отношение эквивалентности, требуется
доказать, что оно рефлексивно, симметрично
и транзитивно.
Очевидно, что для
любого элемента
выполняется
.
Следовательно,
рефлексивно. Если
то
и
принадлежат одному и тому же подмножеству
разбиения, так что и
 Следовательно,
симметрично. Если
и
Следовательно,
симметрично. Если
и
 то
элементы
и
находятся в одном и том же подмножестве
,
а элементы
и
– в подмножестве
то
элементы
и
находятся в одном и том же подмножестве
,
а элементы
и
– в подмножестве
 Так как подмножества разбиения не
пересекаются и элемент
принадлежит одновременно
и
Так как подмножества разбиения не
пересекаются и элемент
принадлежит одновременно
и
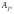 то
то
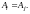 Таким образом,
транзитивно.
Таким образом,
транзитивно.
Всё вышесказанное можно объединить в следующей теореме.
Теорема. Пусть – отношение эквивалентности на множестве Тогда классы эквивалентности отношения формируют разбиение множества И наоборот, при заданном разбиении множества определено отношение эквивалентности такое, что подмножества разбиения являются классами эквивалентности.
