5.2.2 Свойства отношений
Отношение на множестве называется
рефлексивным, если
для всех
;антирефлексивным, если
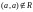для любого
;симметричным, если для всех и , принадлежащих , из следует, что
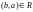;антисимметричным, если для всех и , принадлежащих , из и следует, что
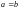;асимметричным, если для всех и , принадлежащих , из следует, что
;транзитивным, если для любых , и
,
принадлежащих
,
из
и
следует, что
.
Заметим, что отношение является асимметричным тогда и только тогда, когда оно одновременно антирефлексивно и антисимметрично.
Если рефлексивное отношение задано ориентированным графом, то каждая вершина имеет петлю, то есть дугу, начинающуюся и заканчивающуюся в одной и той же вершине.
У графа, представляющего антирефлексивное отношение, наоборот, отсутствует петля у любой вершины.
Граф симметричного отношения вместе с дугой из вершины в вершину имеет дугу, направленную в обратную сторону,
Если граф представляет антисимметричное отношение, то при наличии дуги из вершины в несовпадающую с ней вершину , дуга из в обязательно будет отсутствовать.
Для графа асимметричного отношения, кроме отсутствия взаимно обратных дуг между любыми двумя вершинами, у каждой из вершин отсутствуют петли (в графе для антисимметричного отношения у некоторых или у всех вершин петли могут присутствовать).
И, наконец, граф транзитивного отношения устроен так, что вместе с дугами из вершины в вершину и из в у него обязательно будет дуга из в .
Перечислим особенности
матриц, отражающие соответствующие
свойства отношений. Так, если отношение
рефлексивно, то на главной диагонали
матрицы все элементы
равны
единице; в случае, если отношение
антирефлексивно, то элементы
в матрице отношения равны нулю.
Матрица симметричного
отношения будет симметричной, то есть
для любых
выполняется
,
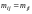или, в матричной записи,
.
В матрице
антисимметричного отношения выполняется
условие: если
и
,
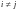то
.
В матрице асимметричного отношения, кроме предыдущего условия, требуется, чтобы на главной диагонали стояли нулевые элементы.
Свойство для матрицы транзитивного отношения будет получено в следующем пункте.
Пример. Свойства отношений из примера в предыдущем параграфе сведены в таблицу
Пример |
Рефл. |
Антир. |
Симм. |
Антис. |
Асимм. |
Транз. |
1 |
+ |
- |
- |
+ |
- |
+ |
2 |
+ |
- |
+ |
- |
- |
+ |
3 |
- |
+ |
- |
+ |
+ |
+ |
4 |
- |
+ |
+ |
- |
- |
- |
5 |
+ |
- |
+ |
- |
- |
+ |
Заметим, что асимметричное отношение всегда будет антисимметричным, обратное утверждение в общем случае будет неверно (см. пример 1).