
- •Глава 5. Элементы дискретной математики
- •5.1.2 Операции над множествами
- •5.1.3 Представление множеств в компьютере
- •5.2.2 Свойства отношений
- •5.2.3 Операции над отношениями
- •5.2.5 Отношение эквивалентности
- •5.2.6 Отношение частичного порядка
- •5.3.3 Разложение булевой функции по переменным
- •5.3.4 Минимизация дизъюнктивных нормальных форм
- •5.3.5 Функциональная полнота
Глава 5. Элементы дискретной математики
5.1 МНОЖЕСТВА
5.1.1 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определённая совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.
Если объект
 является
элементом множества
является
элементом множества
 ,
то говорят, что
принадлежит
и обозначают
,
то говорят, что
принадлежит
и обозначают
 ;
в противном случае говорят, что
не
принадлежит
и обозначают
;
в противном случае говорят, что
не
принадлежит
и обозначают
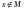 .
.
Пример:
множество натуральных чисел
 ;
;множество целых чисел
 ;
;множество рациональных чисел
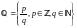 ;
;множество действительных чисел
 .
.
Множество, не
содержащее элементов, называется пустым
и обозначается
 .
.
Основными способами задания множеств являются
перечисление элементов;
характеристический предикат;
порождающая процедура.
Заметим, что перечислением элементов можно задавать только конечные множества, с помощью характеристического предиката и порождающей процедуры можно задавать как конечные так и бесконечные множества. В качестве примера рассмотрим задание множество ненулевых цифр различными способами:
перечисление
элементов
 ;
;
характеристический
предикат:
 ;
;
порождающая процедура:
а)
 ;
;
б) если
и
 ,
то
,
то
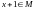 .
.
Множество
 называется
подмножеством
множества
называется
подмножеством
множества
 (обозначается
(обозначается
 ),
если каждый элемент множества
является также элементом множества
.
Если одновременно выполняются включения
и
),
если каждый элемент множества
является также элементом множества
.
Если одновременно выполняются включения
и
 ,
то множества
и
называются равными.
,
то множества
и
называются равными.
Пусть
– конечное множество. Число элементов
множества
называется мощностью
множества и обозначается
 .
.
Множество всех подмножеств множества называется булеаном.
Теорема.
Мощность булеана конечного множества
равно
 .
.
Доказательство данной теоремы будет проведено позднее.
Декартово произведение множеств и – это множество всех упорядоченных пар элементов, первый из которых принадлежит множеству , а второй – множеству :
 .
.
5.1.2 Операции над множествами
Пусть и – множества. Тогда над этими множествами можно определить определённые операции.
Объединением
множеств
и
называется множество, обозначаемое
 ,
содержащее все элементы, которые
принадлежат или множеству
,
или множеству
,
или обоим множествам одновременно.
,
содержащее все элементы, которые
принадлежат или множеству
,
или множеству
,
или обоим множествам одновременно.
Например, объединением
множеств и
и
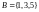 будет
будет
 .
.
Пересечением
множеств
и
называется множество, обозначаемое
 ,
содержащее все элементы, которые
принадлежат обоим множествам
и
одновременно.
,
содержащее все элементы, которые
принадлежат обоим множествам
и
одновременно.
Так, пересечением
множеств
и
будет
 .
.
Разностью множеств
Разностью множеств
и
будет
 .
Заметим, что в общем случае
.
Заметим, что в общем случае .
В данном примере
.
В данном примере
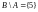 .
.
Симметрической
разностью
и
называется множество, обозначаемое
 ,
содержащее все элементы, только одному
из множеств
или
.
,
содержащее все элементы, только одному
из множеств
или
.
Симметрической
разностью множеств
и
будет .
.
Легко заметить (и
доказать), что выполняются соотношения .
.
Дополнением множества
называется множество
 ,
которое содержит все элементы, не
принадлежащие
.
В этом случае, заранее должно быть
определено некоторое универсальное
множество
,
которое содержит все элементы, не
принадлежащие
.
В этом случае, заранее должно быть
определено некоторое универсальное
множество
 ,
содержащее все возможные элементы.
,
содержащее все возможные элементы.
Для иллюстрации операций над множествами часто используются диаграммы Венна (называемые также кругами Эйлера), в которых исходные множества изображаются фигурами, а результат операции каким-либо образом выделяется.
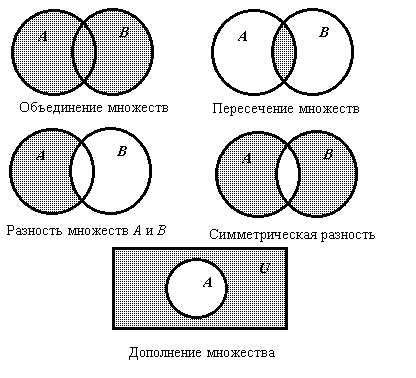
Рис.5.1
Операции над множествами обладают следующими важными свойствами:
свойства идентичности:
 ;
;свойства доминирования:
 ;
;свойства идемпотентности:
 ;
;свойства дополнения:
 ;
;свойства коммутативности:
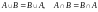 ;
;свойства ассоциативности:
 ;
;
свойства дистрибутивности:
 ;
;
законы де Моргана:
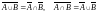 .
.
Так как операции
объединения и пересечения обладают
свойствами ассоциативности, то можно
ввести операции объединения и пересечения
нескольких множеств. Так, объединением
множеств
 называется множество
называется множество
 ,
содержащее все элементы, принадлежащие
хотя бы одному из множеств. Аналогично,
пересечением множеств
называется множество
,
содержащее все элементы, принадлежащие
хотя бы одному из множеств. Аналогично,
пересечением множеств
называется множество
 ,
содержащее все элементы, принадлежащие
всем множествам.
,
содержащее все элементы, принадлежащие
всем множествам.
