Московский Государственный Университет Приборостроения и Информатики

Кафедра: «Инновационные технологии в приборостроении, микро- и оптоэлектронике»

Дюжиков В.И.

Оптическое материаловедение

Курс лекций

часть 2

Направление подготовки 200400 «Оптотехника»

Профиль подготовки бакалавров 200.400.04

Оптические технологии и материалы

Москва 2012

Оптические кристаллы

В современной оптоэлектронике они являются основными оптическими материалами, так как обладают многими специфическими свойствами, которые не свойственны традиционному оптическому стеклу. Одновременно расширяется их применение в классической оптике, так как их оптические свойства изменяются в более широких пределах, чем у оптического стекла.

Структура кристалла

Оптическими кристаллами называют вещества, имеющие правильное периодическое внутреннее расположение частиц (молекул, атомов, ионов) и прозрачные в определенной части светового излучения.

Кристаллы в отличие от стекла обладают так называемым дальним порядком. В стекле же, как и в жидкости наблюдается только ближний порядок, дальний порядок нарушен.

В кристалле правильные ряды частиц в пространстве образуют кристаллическую структуру.

Во всех кристаллах частицы выстраиваются симметричными правильными рядами. В реальных же кристаллах это закономерное чередование частиц всегда немного нарушено из-за их теплового движения, возбуждения и т.д.

Будем рассматривать кристаллы идеальными, когда в его структуре нет нарушений. Все одинаковые частицы расположены одинаковыми параллельными рядами, которые надо представлять себе бесконечными. Расстояние между частицами в большинстве кристаллов составляет несколько десятых долей нанометра.

1нм=10^-9 м; 1нм=10^-3 мкм

Поэтому даже при длине 1мм в кристалле располагается 10⁷атомов.

Кратчайшее расстояние между одинаковыми точками в ряду называется элементарной трансляцией или периодом идентичности.

Рисунок 1. Симметричный бесконечный ряд с трансляцией «а».

Иногда употребляют название период трансляции или параметр ряда.

Если в этом ряду все точки сдвинуть на один период идентичности, то все одинаковые точки передвинутся, ряд совмещается сам с собой, так что вид его не нарушится. Так производятся симметричные преобразования: ряд симметрично сдвинут на один период трансляции a.

Характеристикой этого ряда являются кратчайшие трансляции а. Одинаковые точки, связанные между собой трансляциями а в бесконечном ряду, называются узлами ряда.

Узлы не обязательно должны совпадать с материальными частицами, это могут быть одинаковые точки между частицами.

Т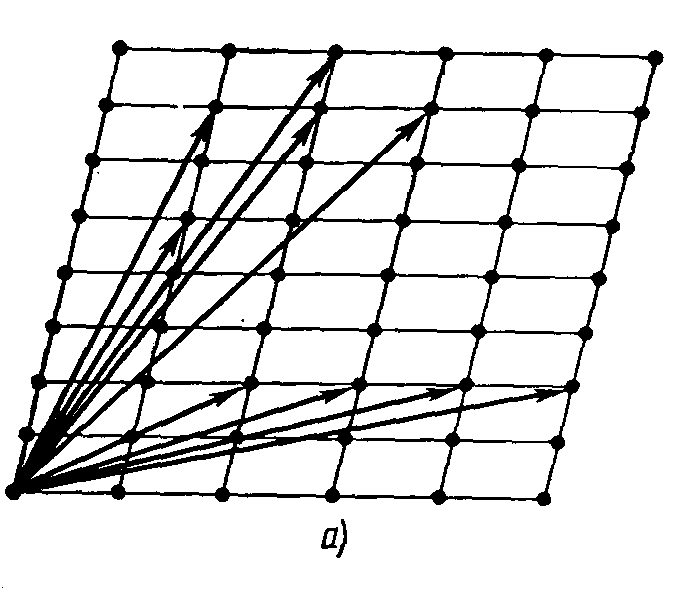 рансляцию можно осуществить не только в ряду, но и между рядами. Так образуется плоская двукоординатная сетка.

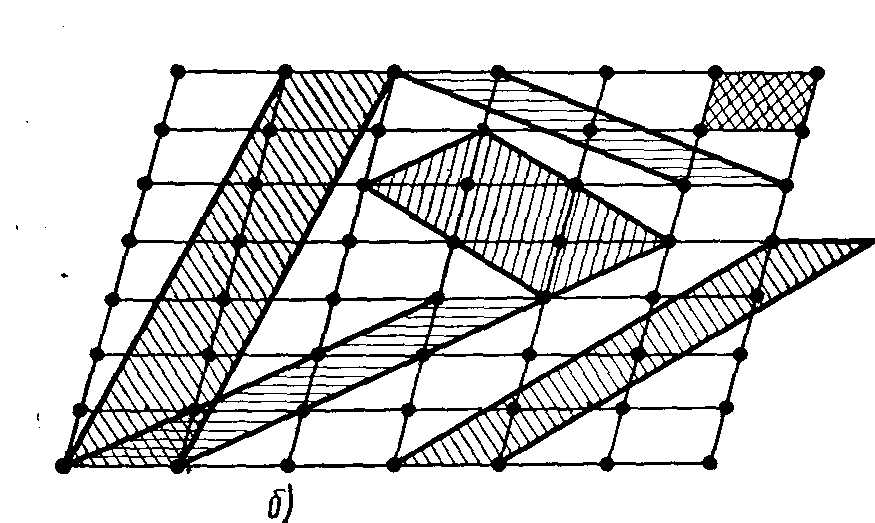
Рисунок 2. Плоская сетка.

а – различные основные трансляции; б - различные элементарные ячейки.

Совокупность этих точек образует трехмерную пространственную решетку.

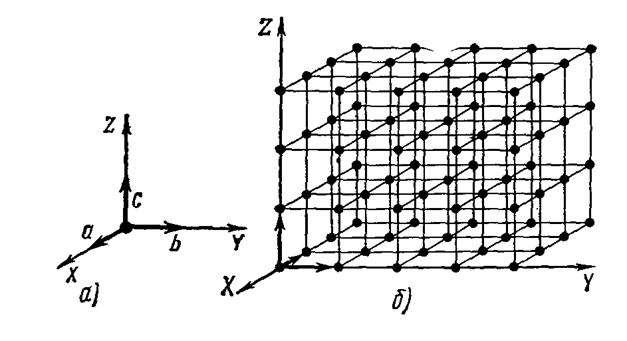
Рисунок 3. Пространственная решетка

Наименьшая часть решетки, отображающая форму всей кристаллической структуры вещества (кристалла) называется элементарной ячейкой, как правило это параллепипед.

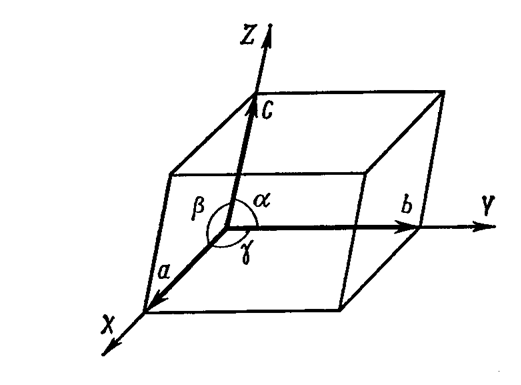
Рисунок 4. Элементарный параллелепипед.

Структура кристалла – это конкретное расположение частиц в пространстве. Пространственная решетка – это способ представления периодичности повторения в пространстве отдельных частиц или групп частиц.

Закон постоянства углов кристалла. Формула Вульфа-Брэгга.

Когда образуется кристалл, частицы выстраиваются в закономерные симметричные ряды сетки решетки. Грани образующих их кристаллических многогранников соответствуют плоскостям, составленным из материальных частиц, а ребра кристалла – линиям пересечения этих плоскостей. Очевидно, любой ряд в структуре соответствует возможному ребру кристалла, а любая плоскость – возможной грани кристалла. Грани образуются параллельными самим себе.

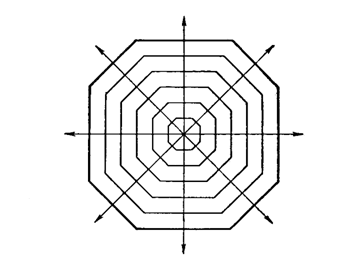
Рисунок 5. Схема параллельного нарастания граней кристалла.

Стрелками изображены нормали к граням.

Н. Стенон в 1669 году открыл закон постоянства углов: во всех кристаллах данного вещества, при одинаковых условиях, углы между соответствующими гранями кристаллов постоянны.

Кристаллы разных веществ отличаются друг от друга внешней формой, у кристаллов одного и того же вещества внешний облик (габитус) может оказаться совсем различным, но углы между соответствующими гранями останутся постоянными.

Закон постоянства углов позволяет свести все многообразие пространственных многогранников к совокупности углов между гранями и изобразить их с помощью проекции.

Этот закон сыграл огромную роль в развитии кристаллографии. До открытия отражений рентгеновских лучей кристаллы характеризовались и отличались друг от друга только по углам между их гранями.

Основным методом диагностики в кристаллографии стало измерение углов в кристалле между гранями на ренгенгониометре (отраженный или преломляющий). Схема дифракции рентгеновских лучей атомными плоскостями дана на рисунке 6.

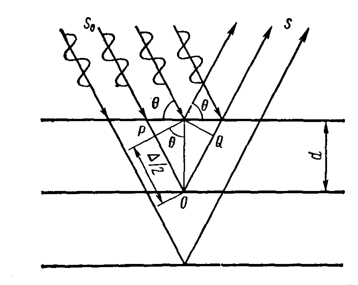
Рисунок 6. К выводу условия Вульфа-Брэгга.

Из схемы видно разность хода между падающими и отраженными лучами равна

=PO+OQ=2PQ=2dsin

Если =n, где n=1,2,3….,  - длина волны рентгеновского излучения (=0,154 нм), то наблюдается максимум интенсивности отраженных лучей. 2dsin=n (n=1,2,3…) Равенство выражает закон Вульфа—Брэгга, открытый в 1913г.

Угол падения  дает максимальное отражение не при любом значении, а при тех, когда выполняется условие Брэгга. Этот угол обозначается _Б.

Для каждого кристалла и для каждой грани этот угол имеет определенное значение. Для известных кристаллов эти значения приведены в соответствующих кристаллографических таблицах.

Измерение производится с помощью рентгеновского гониометра, принцип работы которого аналогичен гониометру, работает на отражение, только вместо источника света применяется рентгеновская вакуумная трубка, источник рентгеновского излучения, а в качестве приемника излучения применяется детектор, аналогичный камере Вильсона, счетчику Гейгера или сцинтилляционный оптический датчик.

С помощью него можно измерить межатомное расстояние a

Метод кристаллографического индицирования атомных плоскостей.

К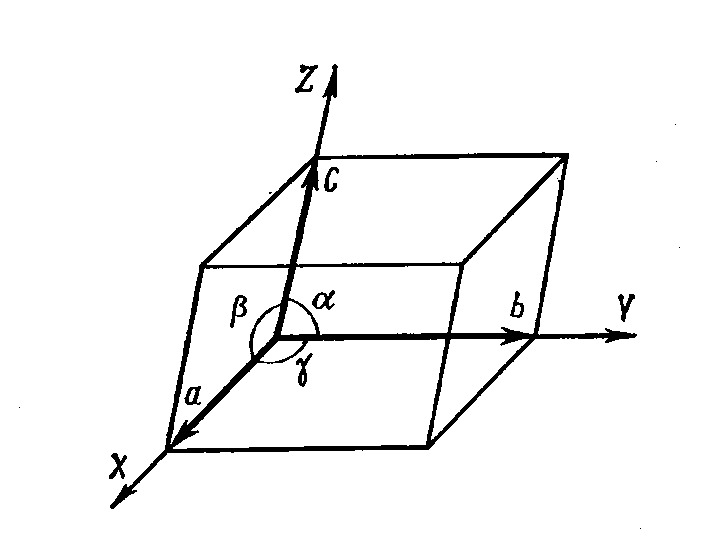 ристаллическая решетка характеризуется шестью параметрами элементами ячейки: длинами ребер a,b,c и углами ,,

В общем случае:

a≠b≠c

≠≠

Рисунок 7.Элементарный параллелепипед.

Для описания кристаллических многогранниковых структур применяется метод кристаллографического индицирования, удобный для всех кристаллографических систем, независимо от того прямоугольные они или косоугольные, одинаковые у них отрезки или разные.

Расстояние в кристаллах будем измерять в длинах ребер a,b,c. Тогда

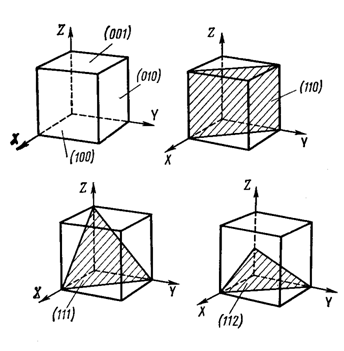
Рисунок 8. Символы некоторых плоскостей в кубической решетке

1. Плоскость или грань, перпендикулярная оси х, записывается (100)

2. Плоскость или грань, перпендикулярная оси у, записывается (010)

3. Плоскость или грань, перпендикулярная оси z, записывается (001)

Для грани перпендикулярной оси х; (hkl)=(100): h=1, k=0, l=0

hkl- атомная плоскость

a/h;b/k;c/l – отрезки, отсекаем плоскостью hkl на осях координат x,y,z

h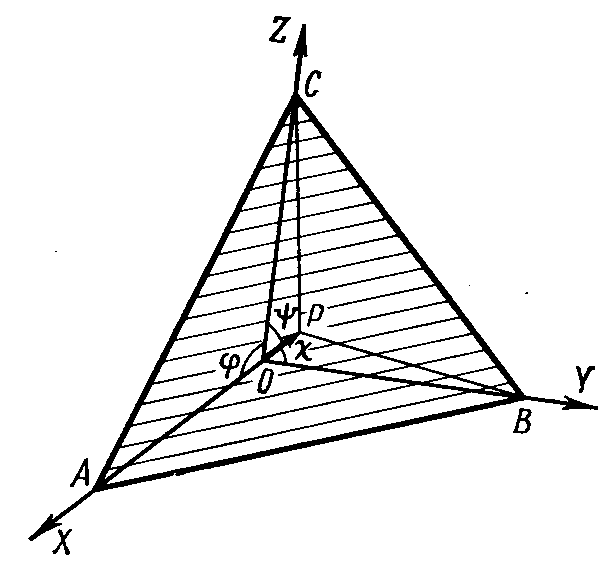 ,k,l- простые целые числа

hkl

c/l

a/h

b/k

Рисунок 9. Индексы Миллера для плоскостей hkl

Обозначение (hkl) носит название индексов Миллера. Они показывают сколько раз плоскость данного типа пересекает оси кристалла в данной элементарной ячейке.

Наряду с обозначениями кристаллографических плоскостей в круглых скобках задается направление перпендикулярное к этим плоскостям.

Индексы этого перпендикулярного направления такие, как у плоскости <hkl>,[hkl].

Символы некоторых направлений в плоской сетке и осей координат.

Все направления в кристалле равнозначны. Тогда направления ряда определяются двумя точками: началом координат и любым узлом ряда символ ряда пишут в квадратных скобках [mpn] (Рисунок 10).

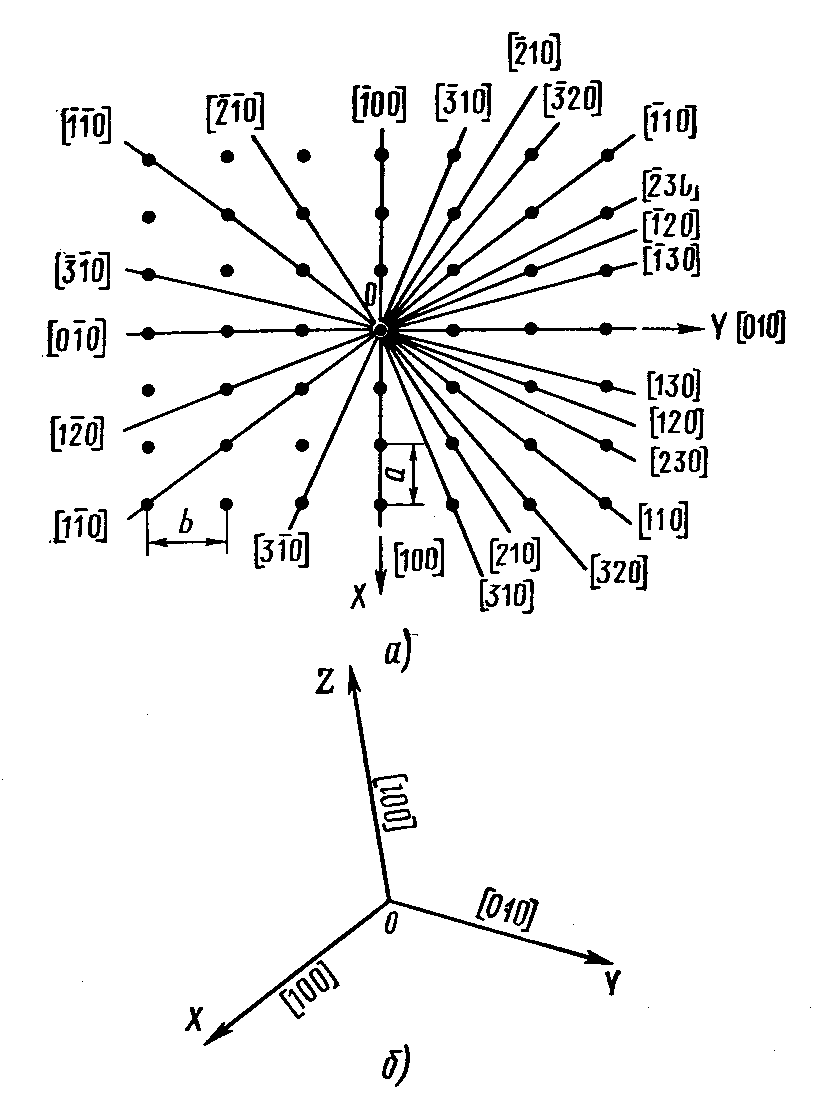
Рисунок 10. Символы некоторых направлений в плоской сетке (а) и осей координат (б)

Главное преимущество такой индексации: символы осей координат не зависят от углов между осями координат и от осевых отрезков, они одинаковы в любой системе координат.

Кристаллографические проекции.

Форму кристаллографического многогранника, расположение его элементов симметрии, анизотропию свойств, можно охарактеризовать набором углов между гранями. В кристаллографии часто пользуются углами между нормалями граней. Именно эти углы определяются по гониометрическим измерениям и рентгенограммам. В этом случае, вместо прямоугольной системы координат используются сферические координаты (Рисунок 11).

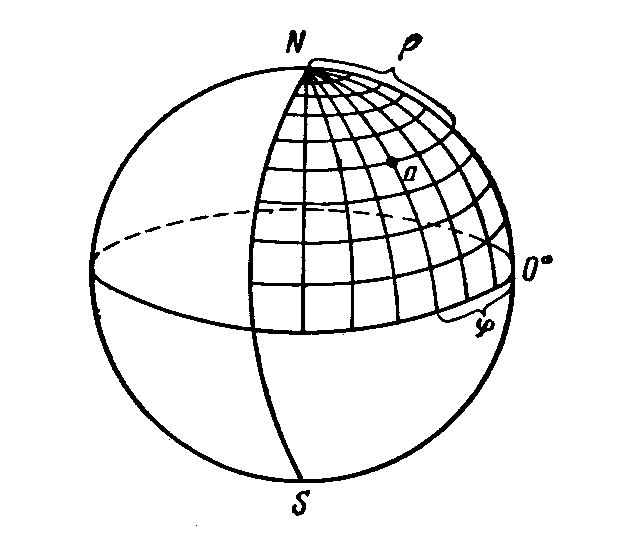
Рисунок 11. Сферические координаты на поверхности сферы проекций.

Положение любой точки в сферической системе координат характеризующимися двумя сферическими координатами (р - полярное расстояние, -долгота). При использовании сферической системы координат каждая точка проецируется на экваториальную плоскость.

Сферическая проекция кристалла наглядна, но для практического применения используются и другие проекции кристалла. Наиболее употребительна сетка Вульфа - стереографическая проекция всех меридианов и параллелей, нанесённых на поверхность сферы (Рисунок 12).

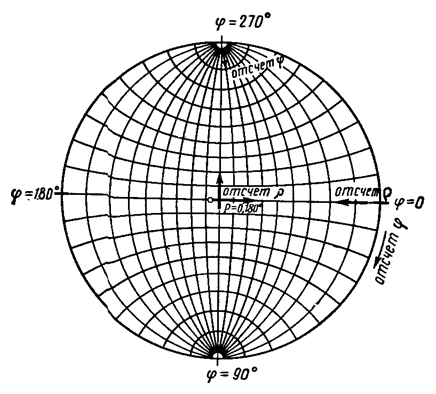
Рисунок 12. Схема сетки Вульфа и отсчёт углов по ней.

Элементы симметрии кристаллов, многогранников.

Симметрия форм кристалла отражает симметрию их физических свойств.

Симметричной фигурой называется многогранник, который может совместиться сам с собой в результате симметричных преобразований.

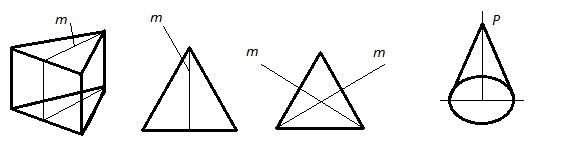
Рисунок 13. Плоскость (m) и ось (P) симметрии.

Используются понятия плоскостей симметрии, центров симметрии осей симметрии - воображаемых плоскостей, точек и линий, называемых элементарными симметриями.

Симметрия структуры кристаллов.

Все разнообразие кристаллов сводится к следующим семи основным кристаллографическим системам, или сингониям.

Сингония - сходноугольность (сходство углов).

Первая система: - Кубическая

Узлы кристаллической решетки создают куб, у которого параметры решетки одинаковы a=b=c, а углы ===90⁰

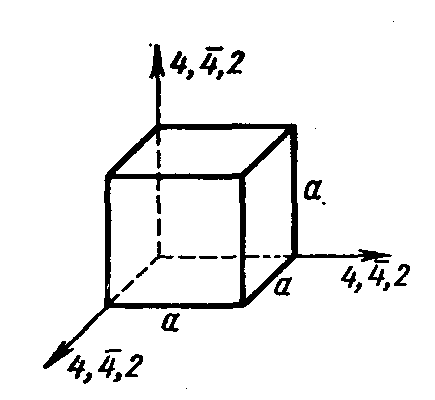
Рисунок 14. Кубическая ячейка.

В этой решетке кристаллизуются все кристаллы n-ых проводников (Si, Ge, GaAs, Cu), щелочно-галлоидные кристаллы (LiF, NaCl, KCl).

Кристаллы с кубической решеткой относятся к высшей категории симметрии. В этих кристаллах анизотропия свойств в различных направлениях выражена слабо. Многие физические свойства в этих кристаллах изотропны: теплопроводимость, электропроводимость,

показатель преломления одинаковых во всех направлениях.

Внешняя форма этих кристаллов, как правило, изометрична, т.е. развита примерно одинакова по всем направлениям. Кристаллы имеют форму куба (6-граней), октаэдра (8-граней). В этих кристаллах анизотропия таких свойств, как упругость и электрооптический эффект развиты гораздо слабее, чем у кристаллов других категорий.

Кристаллографические категории, сингонии и системы координат.

Плоскости симметрии, оси симметрии и центры симметрии образуются в кристаллах в разных сочетаниях. Например: у кристаллов с кубической решеткой (у полупроводников и щелочно-галлоидных кристаллов) один и тот же набор элементов симметрии: плоскостей симметрии m (P) - 9, 3 оси четвертого порядка 4(L₄), 4 оси третьего порядка 3(L₃), 6 осей второго порядка 2(L₂) и один центр симметрии (С), единичных направлений нет.

Категории симметрии: их три высшая, средняя и низшая. Это деление на категории происходит по симметрии и числу единичных направлений кристалла. Симметрия куба или октаэдра характерна для кристаллов высшей категории. (См. Кубическую решетку)

Кристаллы высшей категории: к ним относятся кристаллы, имеющие тетрагональную, тригональную и гексагональную решетки.

Тетрагональная – главная ось симметрии 4 или ; a=b≠c, ===90

Форма элементарной ячейки—призма с квадратным основанием.

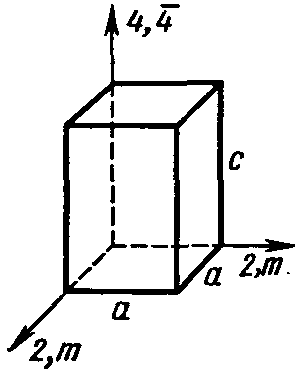
Рисунок 15. Тетрагональная ячейка.

К тетрагональной системе относятся кристаллы KDP и ADP (искусственные)

(дигидрофосфат калия и дигидрофосфат амония), селаита MgF₂.

Тригональная – главная ось симметрии 3 или ; a=b≠c, ==90, =120

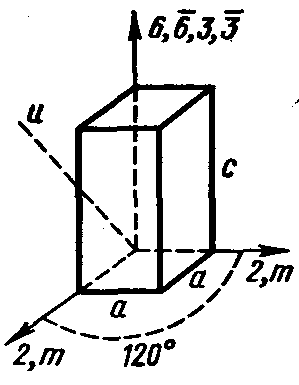
Рисунок 16. Тригональная ячейка.

Форма элементарной ячейки—призма с ромбическим основании с углом 120

К тригональной системе относятся кристаллы кальцитаCaCO₃(природные и искусственные), кварца (-SiO₂), ниобата и танталата лития(LiNbO₃ и LiTaO₃).

Гексагональная - главная ось симметрии 6 или

a=b≠c, ==90, =120

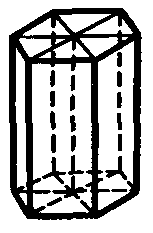
Рисунок 17. гексагональная ячейка.

Форма элементарной ячейки – призма с ромбическим основанием с углами 120. Три такие призмы составляют шестигранную призму, уже не примитивную, гексагональную ячейку. К гексагональной системе относятся кристаллы кварца (-кварц).

К низшей категории относятся три сингонии: ромбическая, моноклинная и триклинная.

Ромбическая – три оси 2 и три плоскости m симметрии a≠b≠c, ===90

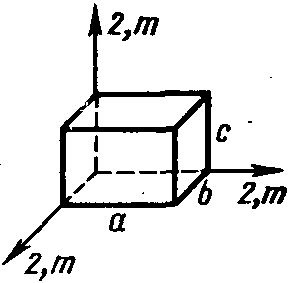
Рисунок 18. Ромбическая ячейка.

К ромбической системе относится кристаллическая сера.

Моноклинная – ось 2 или плоскость m симметрии, a≠b≠c, ===90

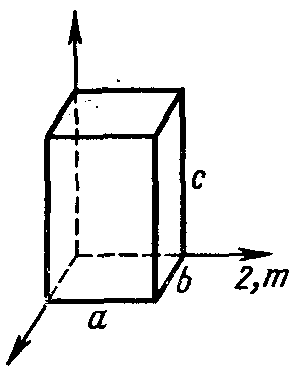
Рисунок 19. моноклинная ячейка.

К моноклинной системе относятся кристаллы слюды и гипса.

Т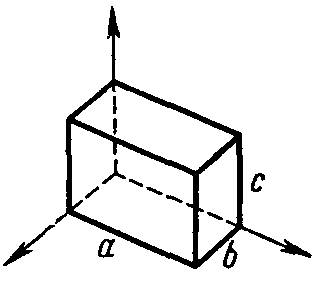 риклинная – ось 1 или симметрия, a≠b≠c, ≠≠=90

Рисунок 20. триклинная ячейка.

К триклинной системе относятся кристаллы двухромистокислого калия (K₂CrO₇)

У всех этих кристаллов наличие правильной кристаллической структуры (пространственной решетки) доказано методами рентгеноструктурного анализа. Состав атомов и структуры кристалла определяют его физико-химические свойства.