Московский государственный университет приборостроения и информатики

Кафедра ''Инновационные технологии в приборостроении, микро- и оптоэлектронике''

Дюжиков В.И

Оптическое материаловедение

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Часть 2

Специальность 200204

(ОПТИЧЕСКИЕ ТЕХНОЛОГИИ И МАТЕРИАЛЫ)

Москва, 2010г.

Дюжиков В.И.

Оптическое материаловедение: лабораторный практикум, часть 2, М.: МГУПИ, 2010, 32 с.

Лабораторный практикум предназначен для студентов специальности 200204 «Оптические технологии и материалы» и направления подготовки 200200 «Оптотехника».

©МГУПИ, 2010

Определение и исследование спектральных характеристик пропускания кристаллов.

Цель работы - изучение и освоение на практике измерения коэффициента пропускания потока излучения через оптический кристалл.

1. Основные положения

При прохождении потока излучения через оптический кристалл наблюдается его ослабление из-за потерь на отражение от поверхностей кристалла и на поглощение в его массе.

Поглощение и отражение светового потока зависят от показателя преломления оптического кристалла, длины волны падающего излучения, от примесей и других дефектов материала.

Согласно закону сохранения энергии для светового потока монохроматического излучения Ф, падающего на кристалл, выполняется условие:

Ф= Ф_ρ+ Ф_α + Ф_τ , (1.1)

где Ф_ρ- отраженный поток,

Ф_α- поглощенный поток,

Ф_τ- пропущенный кристаллом поток.

Отношение каждого из потоков Ф_ρ, Ф_α и Ф_τ к падающему потоку монохроматического излучения называется соответственно:

коэффициент отражения 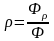; (1.2)

показатель поглощения ; (1.3)

коэффициент пропускания ; (1.4)

Следовательно: (1.5)

Различают:

1)спектральный коэффициент пропускания τ_λ излучения данной длины волны λ;

2)интегральный коэффициент пропускания τ излучения кристаллов, прозрачных в видимой части спектра (λ=380…760 нм) и кристаллов, непрозрачных в видимой части спектра (в рабочей области ультрафиолетовой или инфракрасной). Этот коэффициент характеризует прозрачность материала.

1.1. Спектральное пропускание Спектральный коэффициент пропускания τλ определяется как отношение прошедшего через кристалл потока излучения Фλτ к падающему Фλ .

(1.6)

Величина 1-τ_λ характеризует полные потери света, обусловленные поглощением и отражением.

Спектральный коэффициент внутреннего (чистого) пропускания τ_iλ определяется как отношение выходящего потока излучения (Ф_λ)_ex к входящему потоку (Ф_λ)_in . При этом потери на отражение от граничных поверхностей кристалла исключены:

(1.7)

Между коэффициентами внутреннего пропускания τ_iλ и коэффициентом пропускания τ_λ соблюдается соотношение:

, (1.8)

где R- коэффициент, учитывающий потери света, обусловленные только отражением на двух поверхностях.

Коэффициент R определяется выражением:

(1.9)

Зависимость коэффициента отражения от показателя преломления выражается уравнением Френеля (для одной поверхности раздела кристалл-воздух);

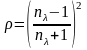, (1.10)

где n_λ –показатель преломления кристалла в рабочей области спектра: ультрафиолетовой, видимой, инфракрасной.

Граница пропускания характеризуется длиной волны λ_гр., при которой спектральный коэффициент внутреннего пропускания τ_iλ равен 0,5.

Условие прозрачности кристаллов может быть выражено соотношением:

, (1.11)

где h- постоянная Планка;

c- скорость света в вакууме;

λ- длина волны излучения;

то есть энергия кванта излучения E должна быть меньше ширины запрещенной зоны Е_g .

Из этого соотношения легко выводится граничное условие прозрачности:

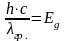(1.12)

При этом условии энергия кванта с длиной волны λ = λ_гр. окажется достаточной для возбуждения электронов и переброса их из валентной зоны в зону проводимости. Этот переброс будет сопровождаться поглощением энергии электромагнитного излучения. Из граничного условия τ_iλ=0,5 находим величину граничной длины волны λ_гр., под которой понимают границу начала пропускания света веществом. При значениях λ > λ_гр вещество прозрачно, т.к. энергия кванта излучения 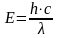окажется меньше Е_g. При значениях λ < λ_гр кристалл непрозрачен, т.к. энергия кванта излучения окажется больше ширины запрещенной зоны Е_g.

Подставляя h и c в формулу (1.12) получим соотношение:

Зная ширину запрещенной зоны, легко определить границу прозрачности любого кристалла.

Определение спектральных характеристик пропускания кристаллов производится на автоматическом спектрофотометре СФ-56А с компьютером.