
- •Прямоугольные (Декартовы) координаты на прямой, на плоскости и в пространстве. Косоугольные системы координат.
- •Расстояние между двумя точками прямой, плоскости и в пространстве.
- •Деление отрезка в заданном отношении
- •Полярная система координат. Сферическая система координат.
- •Переход от декартовой системы координат к полярной. И обратно.
- •Преобразование координат для прямоугольной системы координат.
- •Алгебраическая линия и её порядок. Теорема об инвариантности порядка
- •Уравнение прямой на плоскости, проходящей через две заданные точки.
- •Уравнение прямой с угловым коэффициентом. Пучок прямых.
- •Уравнение прямой, проходящей через заданную точку в заданном направлении.
- •Угол между двумя прямыми.
- •Условия параллельности и перпендикулярности прямых.
- •Уравнение прямой в отрезках на осях.
- •Общее уравнение прямой на плоскости.
- •Окружность. Общее и каноническое уравнения окружности.
- •Эллипс. Каноническое уравнение эллипса и его свойства.
- •Парабола. Каноническое уравнение параболы и его свойства.
- •Гипербола. Каноническое уравнение гиперболы и его свойства.
- •Окружность, эллипс, гипербола и парабола как алгебраические линии второго порядка.
- •20. Геометрический вектор (длина вектора, нуль-вектор, равенство геометрических векторов, коллинеарность и компланарность). Координатные орты.
- •21. Линейные операции с геометрическими векторами. Координаты геометрического вектора. Радиуса-вектор.
- •23. Действия с геометрическими векторами в координатной форме.
- •24. Признак коллинеарности векторов.
- •25. Скалярное произведение геометрических векторов и его свойства.
- •26. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
- •26,Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
- •27.Общее уравнение прямой на плоскости в представлении геометрических векторов.
- •28.Каноническое и параметрическое уравнения прямой в пространстве. Канонические уравнения прямой
- •29.Общее уравнение плоскости в пространстве.
- •30.Решение неравенств на плоскости
- •31.Матрицы и их классификация. Действия с матрицами. Экономические примеры.
- •32.Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».
- •33.Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.
- •34.Свойства определителя. Терема об определителе произведения квадратных матриц.
- •35.Обратная матрица. Теорема существования и единственности обратной матрицы.
- •Свойства обратной матрицы:
- •36.Элементарное преобразование матрицы. Элементарное преобразования матрицы как умножение матриц.
- •37.Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.
- •38.Транспонирование и его свойства.
- •39.Система линейных уравнений и её решение.
- •40.Теорема об элементарных преобразованиях системы линейных уравнений. Метод Гаусса для решений совместной системы линейных уравнений.
- •41.Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.
- •42.Теорема о решении однородной системы линейных уравнений.
- •43.Теорема о числе решений совместной системы линейных уравнений.
- •44.Решение квадратной системы линейных уравнений с помощью обратной матрицы.
- •Расстояние между двумя точками прямой, плоскости и в пространстве.
41.Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.
Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.
Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:
x1=0 , x2=0 , ..., xn=0.
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет не одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной , если она имеет больше одного решения.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Система линейных уравнений может быть представлена в матричной форме как:

или:
![]() .
.
Здесь ![]() —
это матрица системы,
—
это матрица системы, ![]() —
столбец неизвестных, а
—
столбец неизвестных, а ![]() —
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
—
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
42.Теорема о решении однородной системы линейных уравнений.
Теорема
(о линейном решении однородных
систем).
Пусть ![]() —
решения однородной системы (1),
—
решения однородной системы (1), ![]() —
произвольные константы. Тогда
—
произвольные константы. Тогда ![]() также
является решением рассматриваемой
системы.
также
является решением рассматриваемой
системы.
Теорема
(о структуре общего решения).
Пусть
![]() ,
тогда:
,
тогда:
если
 ,
где
,
где  —
число переменных системы, то существует
только тривиальное решение;
—
число переменных системы, то существует
только тривиальное решение;если
 ,
то существует
,
то существует  линейно
независимых решений рассматриваемой
системы:
линейно
независимых решений рассматриваемой
системы:  ,
причём её общее
решение имеет
вид:
,
причём её общее
решение имеет
вид:  ,
где
,
где  —
некоторые константы.
—
некоторые константы.
Теорема
(об общем решении неоднородных
систем).
Пусть
![]() ,тогда:
,тогда:
если , где — число переменных системы , то решение (2) существует и оно единственно;
если , то общее решение системы (2) имеет вид
 ,
где
,
где  —
общее решение системы (1), называемое общим
однородным решением,
—
общее решение системы (1), называемое общим
однородным решением,  —
частное решение системы (2),
называемое частным
неоднородным решением.
—
частное решение системы (2),
называемое частным
неоднородным решением.
43.Теорема о числе решений совместной системы линейных уравнений.
?
44.Решение квадратной системы линейных уравнений с помощью обратной матрицы.
Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X1 - n не будет равен нулю. Посчитаем этот определитель. Если он равен нулю, то система не будет иметь однозначного, единственного решения и программа не будет решать дальше и выдаст сообщение об ошибке. Если определитель не равен нулю, то будем решать дальше методом обратной матрицы. Записанную Вами систему можно представить в виде произведения матриц: A × X = B, где X - матрица, содержащая искомые Вами решения системы уравнений. Найдем матрицу, обратную матрице A, как известно - А-1 × A = E, где Е - единичная матрица (квадратная матрица с единицами на главной диагонали), эквивалент '1' в матричном исчислении. Домножим обе части уравнения слева на А-1. А-1 × A × X = А-1 × B. Е × X = А-1 × B. X = А-1 × B.
Пример
- x 1 |
+ 2x 2 |
|
= 6 |
- x 1 |
+ 3x 2 |
+ 7x 3 |
= 9 |
- x 1 |
+ x 2 |
+ x 3 |
= 3 |
Решение
Найдем определитель главной матрицы, составленной из коэффициентов при X1 - n:
|
= -8 |
|
Определитель главной матрицы системы уравнений не равен нулю, следовательно данная система уравнений имеет единственное решение. Найдем его. Согласно описанному выше методу необходимо найти матрицу, обратную матрице, составленной из коэффициентов при элементах X1 - n. Для этого достроим главный определитель единичной квадратной матрицей того же порядка справа и последовательно, при помощи элементарных преобразований перенесем единичную квадратную матрицу справа налево. Квадратная матрица, получившаяся при этом справа и будет обратной к главной. Затем домножим обратную матрицу на матрицу В (значения находящие за знаком равенства) и получим матрицу решений.
Достраиваем единичную матрицу справа.
|
|
|
Найдем обратную матрицу.
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
|
|
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1. Квадратная матрица, получившаяся правее единичной и есть обратная к главной.
|
|
|
Умножение обратной матрицы (матрицы - А-1) на матрицу значений за знаком равенства (матрицу - В).
|
× |
|
= |
|
Ответ
x 1 = 0 |
x 2 = 3 |
x 3 = 0 |
Формулы Крамера.
xi=Δi\Δ. Δ1 получена из Δ путем замены первого столбца коэффициентов столбцом из свободных членов.
Записываем матричное равенство в виде: (х1)=1\Δ (А11 А12 А13) × (b1) . записана первая строка,нижние по аналогии. Далее внесем определитель и свободные члены в основную матрицу. Отсюда следует: х1=А11b1+A12b2+… (нижние строки по аналогии). Но А11b1+A12b2+… есть разложение определителя по элементам первого столбца. Значит см.выше.
46Линейное (векторное) пространство. Линейное подпространство.
Векторное (линейное) пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трехмерного пространства.
Векторным пространством (над полем R или C) называют множество L, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные (комплексные) числа, удовлетворяющие следующим условиям:
1) x + y = y + x (коммутативность сложения);
2) (x + y) + z = x + (y + z) (ассоциативность сложения);
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x для любого вектора x;
4) для любого вектора x существует противоположный ему вектор y такой, что x + y = 0;
5) 1∙x = x;
6) α(βx) = (αβ)x (ассоциативность умножения);
7) (α + β)x = αx + βx (дистрибутивность относительно числового множителя);
8) α(x + y) = αx + αy (дистрибутивность относительно векторного множителя).
47Пространство Rn и линейные операции в этом пространстве.
Векторное пространство называют. n-мерным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e1, e2, ...en, а любые n+1 элементов линейно зависимы. Векторное пространство называют бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мерного векторного пространства образуют базис этого пространства. Если e1, e2, ...en - базис векторного пространства, то любой вектор x этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:
x = α1e1 + α2e2 + ... + αnen.
При этом числа α1, α2, ...,αn называют координатами вектора x в данном базисе.
Множество всех векторов 3-мерного пространства образует векторное пространство. Более сложным примером может служить так называемое n-мерное векторное пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел (λ1, λ2, ..., λn). Сумма двух векторов и произведение на число определяются соотношениями:
(λ1, λ2, ..., λn) + (μ1, μ2, ..., μn) =
= (λ1 + μ1, λ2 + μ2, ..., λn + μn),
α∙(λ1, λ2, ..., λn) = (α∙λ1, α∙λ2, ..., α∙λn).
Базисом в этом пространстве может служить, например, следующая система из n векторов: e1 = (1, 0, ..., 0), e2 = (0, 1, ..., 0), ...en = (0, 0, ..., 1).
Система векторов. Линейно зависимые и независимые векторы.
Пусть
имеем векторное пространство V и систему
векторов A={![]() }
(система отличается от множества тем,
что в ней могут быть одинаковые элементы).
Вектор
}
(система отличается от множества тем,
что в ней могут быть одинаковые элементы).
Вектор
![]() называется линейной комбинацией
системы векторов A. Если все скаляры α1
= α2 = α3... = αk = 0, то такая комбинация
называется тривиальной (простейшей),
(и
называется линейной комбинацией
системы векторов A. Если все скаляры α1
= α2 = α3... = αk = 0, то такая комбинация
называется тривиальной (простейшей),
(и
![]() ).
Если хотя б один скаляр отличен от 0, то
такая комбинация называется нетривиальной
).
Если хотя б один скаляр отличен от 0, то
такая комбинация называется нетривиальной
Определение
1.
Система
векторов A называется линейно-независимой,
если только тривиальная линейная
комбинация векторов системы равна
![]() (т.е.
(т.е.![]() )
)
Определение 2. система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная
Критерий линейной зависимости векторов:
Для
того чтобы векторы
![]() (r > 1) были линейно зависимы, необходимо
и достаточно, чтобы хотя бы один из этих
векторов являлся линейной комбинацией
остальных.
(r > 1) были линейно зависимы, необходимо
и достаточно, чтобы хотя бы один из этих
векторов являлся линейной комбинацией
остальных.
Размерность линейного пространства
Линейное пространство V называется n-мерным (имеет размерность n), если в нем:
1) существует n линейно независимых векторов;
2) любая система n + 1 векторов линейно зависима.
Базис линейного пространства. Примеры.
Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
1) система линейно независима.
2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов )
Базис в пространстве R в степени n (канонический базис). Примеры: Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке. Эти векторы называются базисными.
Теорема о разложении вектора по базису.
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Определение.
Пусть а – произвольный вектор ,![]() -
произвольная система векторов. Если
выполняется равенство
-
произвольная система векторов. Если
выполняется равенство
![]() (1)
(1)
то говорят, что вектор а представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора а по базису .
Коэффициенты
линейной комбинации![]() называются
в этом случае координатами вектора а
относительно базиса
называются
в этом случае координатами вектора а
относительно базиса
Линейная оболочка векторов.
Пусть
![]() -
система векторов из векторного
пространства V
над полем P.
-
система векторов из векторного
пространства V
над полем P.
Определение 2: Линейной оболочкой L системы A называется множество всех линейных комбинаций векторов системы A. Обозначение L(A).
Можно показать, что для любых двух систем A и B,
A линейно выражается через B тогда и только тогда, когда
 .
(1)
.
(1)A эквивалентна B тогда и только тогда, когда L(A)=L(B). (2)
Доказательство следует из предыдущего свойства
3 Линейная оболочка любой системы векторов является подпространством пространства V.
Доказательство
Возьмём
любые два вектора
![]() и
и
![]() из
L(A),
имеющие следующие разложения по векторам
из A:
из
L(A),
имеющие следующие разложения по векторам
из A:
![]() .
Проверим выполнимость условий 1) и 2)
критерия:
.
Проверим выполнимость условий 1) и 2)
критерия:
 ,
так как представляет собой линейную
комбинацию векторов системы A.
,
так как представляет собой линейную
комбинацию векторов системы A. ,
так как тоже представляет собой линейную
комбинацию векторов системы A.
,
так как тоже представляет собой линейную
комбинацию векторов системы A.
Рассмотрим
теперь матрицу
![]() .
Линейная оболочка строк матрицы A
называется строчечным пространством
матрицы и обозначается Lr(A).
Линейная оболочка столбцов матрицы A
называется столбцовым пространством
и обозначается Lc(A).
Обратите внимание, что при
.
Линейная оболочка строк матрицы A
называется строчечным пространством
матрицы и обозначается Lr(A).
Линейная оболочка столбцов матрицы A
называется столбцовым пространством
и обозначается Lc(A).
Обратите внимание, что при![]() строчечное
и столбцовое пространство матрицы A
являются подпространствами разных
арифметических пространств Pn
и Pm
соответственно. Пользуясь утверждением
(2),
можно придти к следующему выводу:
строчечное
и столбцовое пространство матрицы A
являются подпространствами разных
арифметических пространств Pn
и Pm
соответственно. Пользуясь утверждением
(2),
можно придти к следующему выводу:
Теорема 3: Если одна матрица получена из другой цепочкой элементарных преобразований, то строчечные пространства таких матриц совпадают.
Векторное представление системы линейных уравнений.
Теорема Кронекера-Капелли.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений
Правило решения произвольной системы уравнений. Найти ранг основной и расширенной матриц,если они не равны,то система несовместна(нет решений). Найти какой-либо базисный минор порядка r. Взять r уравнений из коэффициентов которых составлен базисный минор(остальные отбросить). Коэффициенты которые входят в базисный минор-главные,записываются слева, остальные переносятся в правые части уравнений(свободные). Далее найти выражения главных неизвестных через свободные. Получается общее решение системы. Затем придавая свободным неизвестным произвольные значения получим соответствующие значения главных неизвестных(частные решения исходной системы).
Критерий линейной зависимости векторов в пространстве Rn.
Линейная комбинация векторов Линейной комбинацией векторов называют вектор
![]()
где ![]() -
коэффициенты линейной комбинации.
Если
-
коэффициенты линейной комбинации.
Если ![]() комбинация
называется тривиальной, если
комбинация
называется тривиальной, если ![]() -
нетривиальной.
-
нетривиальной.
Линейная зависимость и независимость векторов
Система ![]() линейно
зависима
линейно
зависима ![]()
 что
что 
Система
линейно
независима 
Критерий линейной зависимости векторов
Для того чтобы векторы (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных. Размерность линейного пространства Линейное пространство V называется n-мерным (имеет размерность n), если в нем:
существует n линейно независимых векторов;
любая система n + 1 векторов линейно зависима.
Обозначения
: n =
dim V; ![]() .
.
Евклидовое пространство.
Определение вещественного евклидова пространства. Вещественное линейное пространство R называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования. I. Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом (х, у). П. Указанное правило подчинено следующим четырем аксиомам: 1°. (х, у) = (у, х) (переместительное свойство или симметрия); 2°. (x1 + x2, у) = (х1 ,у) + (х2, у) (распределительное свойство); 3°. (λх, у) = λ(х, у) для любого вещественного λ; 4°. (х, х) > 0, если х — ненулевой элемент; (х, х) = 0, если х — нулевой элемент. Подчеркнем, что при введении понятия евклидова пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов, произведения элемента на число и скалярного произведения элементов (важно лишь, чтобы эти правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам скалярного произведения). Если же природа изучаемых объектов и вид перечисленных правил указаны, то евклидово пространство называется конкретным.
Нормируемое пространство.
Линейное
пространство
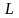 называется нормированным,
если
на нем задана неотрицательная функция
называется нормированным,
если
на нем задана неотрицательная функция
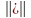 ,
называемая нормой, удовлетворяющая
условиям:
,
называемая нормой, удовлетворяющая
условиям:
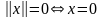 ;
; для
любого
для
любого
 и любого числа
и любого числа
 ;
;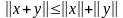 для
любых
для
любых
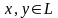 (неравенство треугольника).
(неравенство треугольника).
Ортогональное дополнение и его свойства.
Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.
|A-ᵡE|=0- характерестическое уравнение. См Уравнение в вопросе 46(оно характерестическое)
Теорема: Собственными числами матрицы А являются корни уравнения |A-ᵡE|=0 и только они.
Доказательство . Пусть столбец α -- собственный вектор матрицы А с собственным числом ᵡ . Тогда, по определению, Аα=ᵡα . Это равенство можно переписать в виде . Так как для единичной матрицы Е выполнено Еα=α , то Аα-ᵡЕα=0 . По свойству матричного умножения (А-ᵡЕ)α=Аα-ᵡЕα и предыдущее равенство принимает вид (А-ᵡЕ)α=0(1) Допустим, что определитель матрицы (А-ᵡЕ) отличен от нуля . Тогда у этой матрицы существует обратная (А-ᵡЕ) в минус первой . Из равенства ( 1 ) получим, что α=(А-ᵡЕ)в минус первой×0=0, что противоречит определению собственного вектора. Значит, предположение, что |А-ᵡЕ| неравно нулю, неверно, то есть все собственные числа должны являться корнями уравнения . Пусть ᵡ -- корень уравнения |А-ᵡЕ|=0 . Тогда базисный минор матрицы А-ᵡЕ не может совпадать с определителем матрицы и поэтому ,Rg(А-ᵡЕ)=r<n, n - порядок матрицы A . Уравнение (1) является матричной записью однородной системы линейных уравнений с неизвестными α1,α2…αn , являющимися элементами матрицы-столбца α . Число решений в фундаментальной системе решений равно n-r, что больше нуля. Таким образом, система (1) имеет хотя бы одно ненулевое решение, то есть числу ᵡ соответствует хотя бы один собственный вектор матрицы A . Определитель |А-ᵡЕ| является многочленом степени n от переменного ᵡ , так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.
Линейная функция. Билинейная форма. Квадратичная форма.
Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.
Линейная балансовая модель.
Пусть рассматривается экономическая система, состоящая из n взаимосвязанных отраслей производства. Продукция каждой отрасли частично идет на внешнее потребление ( конечный продукт ), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции ( первый столбец таблицы 1 ) и как ее потребитель ( первая строка таблицы 1 ). Обозначим через xi валовый выпуск продукции i-й отрасли за планируемый период и через yi – конечный продукт, идущий на внешнее для
рассматриваемой системы потребление ( средства производства других экономических систем, потребление населения, образование запасов и т.д. ). Таким образом, разность xi - yi составляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Будем в дальнейшем полагать, что баланс составляется не в натуральном, а в
стоимостном разрезе. Одна из задач балансовых исследований заключается в том, чтобы на базе данных об исполнение баланса за предшествующий период определить исходные данные на планируемый период.
Модель международной торговли.
В
качестве примера математической модели
экономического процесса, приводящей
к понятию собственного вектора и
собственного значения матрицы, рассмотрим
линейную модель обмена (модель
международной торговли).
Процесс
взаимных закупок товаров анализируется
с использованием понятий собственного
числа и собственного вектора матрицы.
Будем полагать, что бюджеты n стран,
которые обозначим соответственно ![]() ,
расходуются на покупку товаров.
,
расходуются на покупку товаров.
Пусть ![]() доля
бюджета
доля
бюджета ![]() ,
которую j–я
страна тратит на закупку товаров у
,
которую j–я
страна тратит на закупку товаров у ![]() -й
страны. Введём матрицу коэффициентов
-й
страны. Введём матрицу коэффициентов ![]() :
:
 .
(1)
.
(1)
Тогда, если весь бюджет расходуется только на закупки внутри страны и вне её (это можно трактовать как торговый бюджет), справедливо равенство
 (2)
(2)
Матрица
(1) со свойством (2), в силу которого сумма
элементов её любого столбца равна
единице, называется структурной
матрицей торговли.
Для
-й
страны общая выручка от внутренней и
внешней торговли выражаетсяформулой ![]() .
(3)
.
(3)
Условие
сбалансированной (бездефицитной)
торговли формулируется естественным
образом: для каждой страны её бюджет
должен быть не больше выручки от
торговли, а в силу условия (2) ![]() или
или
![]() (4)
(4)
Таким образом, условия (4) принимают вид равенств:
 .
(5)
.
(5)
Введём
вектор бюджетов ![]() ,
каждая компонента которого характеризует
бюджет соответствующей страны. Тогда
систему уравнений можно записать в
матричной форме:
,
каждая компонента которого характеризует
бюджет соответствующей страны. Тогда
систему уравнений можно записать в
матричной форме:
![]() .
(6)
.
(6)
Это
уравнение означает, что собственный
вектор структурной матрицы А,
отвечает её собственному значению ![]() ,
состоит из бюджетов стран бездефицитной
международной торговли.
,
состоит из бюджетов стран бездефицитной
международной торговли.
Перепишем
уравнение (6) в виде, позволяющем
определить
:
![]()
. (7)
Комплексные числа. Формула Эйлера. Решение комплексных неравенств на плоскости.
Запись числа z в виде z=x+iy называют алгебраической формой комплексного числа.
Модуль r и аргумент (фи) комплексного числа можно рассматривать как полярные координаты вектора r =ОМ, изображающего комплексное число z=x+iy. Тогда получаем х=rcos(фи), y=r sin(фи). Следовательно, комплексное число z=x+iy можно записать в виде z=r cos(фи)+ir sin(фи) или z=r(cos(фи) +I sin(фи)
Такая запись комплексного числа называется тригонометрической формой.
Модуль r=|z| однозначно определяется по формуле:
R=|z|=x²+y²-все под корнем
Например, |i|=0²+1²(все под корнем)=1. Аргумент фи определяется из формул:
Cos(фи)=x/r sin(фи)=у/r tg(фи)=y/х
При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа z.
Формула Эйлера:
E( в степени i умножить на фи)= cos(фи)+ isin(фи)
Комплексное число z=r(cos(фи)+isin(фи)) можно записать в так называемой показательной (или экспоненциальной) форме z=re в степени iумножить на фи. Где r=|z| - модуль комплексного числа
В силу формулы Эйлера, функция E( в степени i умножить на фи) периодическая с основным периодом 2π. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа.
Линейные операторы как отображения. Образ и ядро линейного оператора.
Определение. Если каждому элементу ᵡ из линейного постранства L ставится в соответствие единственный элемент « y» из линейного постранства M, то говорят, что задан оператор, действующий из постранства L в пространство M (или оператор, действующий в пространстве L, если L совпадает с M). Результат действия оператора A на элемент ᵡ обозначают : у=А(х). Над у,х и лямда знаки вектора. Если элементы ᵡ и у связаны соотношением у=А(х) , то у называют образом ᵡ ; а ᵡ — прообразом у. Множество элементов пространства L, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A). Множество элементов пространства M, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если у=А(х), то х принадлжежит D(A), y принадлжежит Im(A) . Ядром оператора называется множество элементов линейного пространства L, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A).
Взаимно однозначные отображения.
Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.
Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.
Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.
Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:
A(u + v) = A(u ) + A(v) , A(α·u) = α· A(u).
Произведение операторов. Обратный оператор.
Пусть А и В –
линейные операторы, причем А действует
из Е в Е1,
а В действует
из Е1 в Е2 . Произведением ВА операторов А и Вназывается
оператор С,
ставящий в соответствие
элементу ![]() элемент
элемент ![]() из Е2.
Область
определения DC оператора С=ВА состоит
из тех х
из Е2.
Область
определения DC оператора С=ВА состоит
из тех х ![]() DA ,
для которых Ах
DB.
Ясно , что оператор С линеен.
Он непрерывен, если А и Внепрерывны.
Если А и В –
ограниченные операторы, действующие
в нормированных пространствах, то и
оператор С=ВА –
ограничен,
причем
DA ,
для которых Ах
DB.
Ясно , что оператор С линеен.
Он непрерывен, если А и Внепрерывны.
Если А и В –
ограниченные операторы, действующие
в нормированных пространствах, то и
оператор С=ВА –
ограничен,
причем
![]() (3)
Действительно,
(3)
Действительно, ![]() ,
следовательно, выполняется (3).
Сумма
и произведение трех и более операторов
определяются последовательно. Обе эти
операции ассоциативны.
Произведение
оператора А на
число к (обозначается кА)
определяется как оператор, который
элементу х ставит в соответствие
элемент кАх.
Совокупность
Z(E,E1)
всех непрерывных линейных операторов,
определенных на всем Е и
отображающих Е в Е1 (
где Е и Е1
,
следовательно, выполняется (3).
Сумма
и произведение трех и более операторов
определяются последовательно. Обе эти
операции ассоциативны.
Произведение
оператора А на
число к (обозначается кА)
определяется как оператор, который
элементу х ставит в соответствие
элемент кАх.
Совокупность
Z(E,E1)
всех непрерывных линейных операторов,
определенных на всем Е и
отображающих Е в Е1 (
где Е и Е1 ![]() –
фиксированные линейные нормированные
пространства), образует, по отношению
к введенным операциям сложения и
умножения на число, линейное пространство.
При этом Z(E,
E1)
– нормированное пространстово (с тем
определением нормы оператора, которое
было дано выше).
4.
Обратный оператор
Пусть А –
линейный оператор, действующий
из Е в Е1 ,
и DA область
определения, а RA –
область значений этого оператора.
Определение
6. Оператор А называется обратимым, если
для любого у
RA уравнение Ах=у имеет
единственное решение.
Если А обратим,
то любому элементу у
RA можно
поставить в соответствие единственный
элемент х
DA ,
являющийся решением уравненияАх=у.
Оператор, осуществляющий это соответствие,
называется обратным к А и
обозначается А-1.
Теорема
3 [1]. Оператор А-1,
обратный линейному оператору А,
также линеен.
Доказательство.
–
фиксированные линейные нормированные
пространства), образует, по отношению
к введенным операциям сложения и
умножения на число, линейное пространство.
При этом Z(E,
E1)
– нормированное пространстово (с тем
определением нормы оператора, которое
было дано выше).
4.
Обратный оператор
Пусть А –
линейный оператор, действующий
из Е в Е1 ,
и DA область
определения, а RA –
область значений этого оператора.
Определение
6. Оператор А называется обратимым, если
для любого у
RA уравнение Ах=у имеет
единственное решение.
Если А обратим,
то любому элементу у
RA можно
поставить в соответствие единственный
элемент х
DA ,
являющийся решением уравненияАх=у.
Оператор, осуществляющий это соответствие,
называется обратным к А и
обозначается А-1.
Теорема
3 [1]. Оператор А-1,
обратный линейному оператору А,
также линеен.
Доказательство.
Достаточно проверить выполнение равенства
![]() .
Положим Ах1=у1 и Ах2=у2,
в силу линейности А имеем
.
Положим Ах1=у1 и Ах2=у2,
в силу линейности А имеем
![]() (*)
По
определению обратного
оператора А-1у1=х1 и А-1у2=х2,
умножим оба равенства соответственно
на
(*)
По
определению обратного
оператора А-1у1=х1 и А-1у2=х2,
умножим оба равенства соответственно
на ![]() и
и ![]() :
:
![]() .
С
другой стороны из равенства (*) следует
.
С
другой стороны из равенства (*) следует ![]() ,
следовательно,
,
следовательно, ![]() .
Теорема
доказана.
Теорема
4 [3]. (Теорема
Банаха об обратном операторе)
Пусть А –
линейный ограниченный оператор, взаимно
однозначно отображающий банахово
пространство Е на
банахово пространство Е1.
Тогда обратный оператор А-1 ограничен.
Теорема
5 [3]. Пусть Е –
банахово пространство, I –
тождественный оператор в Е,
а А –
такой ограниченный линейный оператор,
отображающийЕ в
себя, что
.
Теорема
доказана.
Теорема
4 [3]. (Теорема
Банаха об обратном операторе)
Пусть А –
линейный ограниченный оператор, взаимно
однозначно отображающий банахово
пространство Е на
банахово пространство Е1.
Тогда обратный оператор А-1 ограничен.
Теорема
5 [3]. Пусть Е –
банахово пространство, I –
тождественный оператор в Е,
а А –
такой ограниченный линейный оператор,
отображающийЕ в
себя, что ![]() .
Тогда оператор (I-A)-1 существует,
ограничен и представляется в
виде
.
Тогда оператор (I-A)-1 существует,
ограничен и представляется в
виде  .
Доказательство.
Так
как
.
Доказательство.
Так
как ![]() ,
то ряд
,
то ряд  сходится.
А так как
сходится.
А так как ![]() для
всех
для
всех ![]() ,
то ряд
,
то ряд  также
сходится. Пространство Е полно,
значит, из сходимости ряда
вытекает,
что сумма ряда
также
сходится. Пространство Е полно,
значит, из сходимости ряда
вытекает,
что сумма ряда  представляет
собой ограниченный линейный оператор.
Для любого n имеем:
представляет
собой ограниченный линейный оператор.
Для любого n имеем: ,
переходя к пределу и учитывая, что
,
переходя к пределу и учитывая, что ![]() ,
получаем
,
получаем  ,
следовательно
,
следовательно  .
Теорема
доказана.
.
Теорема
доказана.
Матричная запись линейных операторов.
Выберем
в пространстве V базис ![]() .
Пусть
.
Пусть ![]() –
произвольный элемент из V и
–
произвольный элемент из V и 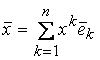 –
разложение
по
данному базису. Пусть А –
линейный оператор из
–
разложение
по
данному базису. Пусть А –
линейный оператор из ![]() .
Тогда А
.
Тогда А А
А![]() .
Полагая, что
.
Полагая, что
А![]() (7.1)
(7.1)
получим
А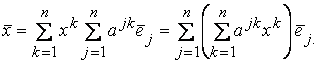
Таким
образом, если ![]() А
и
элемент
А
и
элемент ![]() имеет
координаты
имеет
координаты ![]()
![]() ,
то
,
то
![]() (7.2)
(7.2)
Рассмотрим
квадратную матрицу А
с элементами ![]() :
: ![]()
![]() Эта
матрица называется матрицей
линейного оператора в заданном базисе
Эта
матрица называется матрицей
линейного оператора в заданном базисе ![]() .
.
Наряду
с ранее указанным способом записи
линейного оператора А используется,
при заданном базисе
,
следующая матричная форма: ![]() ,
причем, если
,
причем, если ![]() ,
то
,
то ![]() ,
где
,
где ![]() ,
, ![]() ,
определяется с помощью соотношения
(7.2), а элементы
матрицы А определяются
по формулам (7.1).
,
определяется с помощью соотношения
(7.2), а элементы
матрицы А определяются
по формулам (7.1).
