1. Прямоугольные (Декартовы) координаты на прямой, на плоскости и в пространстве. Косоугольные системы координат.

Прямую линию с указанным на ней направлением, началом отчета и единицей масштаба назовем числовой осью. Каждому действительному числу Х на числовой оси соответствует единственное число, которое называется координатой данной точки.

Здесь числа х₂>х₁>0, х₃<0.

х₃, х₁, х₂, х - координаты точек Q, F, N, M соответственно. Записывают:

Q (х₃), F (x₁), N(x₂), M (x).

Точки F и N ограничивают отрезок FN. Очевидно, его длина | FN | = х₂- х_1. Две взаимно перпендикулярные оси на плоскости с общим началом и одинаковой единицей масштаба образуют декартову прямоугольную систему координат на плоскости. Одна из осей - ось абсцисс Ох, другая - ось ординат Оу.

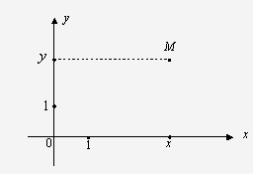
Каждой точке плоскости соответствует единственная пара чисел х, у.

x, у называют координатами точки М и записывают М (х, у).

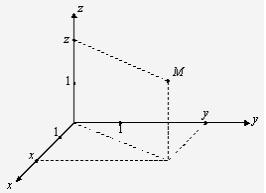
В пространстве декартова прямоугольная система координат представляет собой совокупность трех взаимно перпендикулярных осей с общим началом и одинаковой единицей масштаба. Это ось абсцисс Ох, ось ординат Оу и ось аппликат Оz. Каждая точка пространства М имеет координаты х, у, z. Записывают:М (х, у, z).

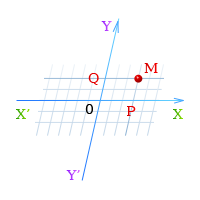
Косоугольная система координат (она наиболее сходна с прямоугольной) строится так: Проводятся две не перпендикулярные прямые X`X,Y`Y (оси координат), а дальше поступают также, как и при построении прямоугольной системы координат.

Т.е. положение точки M на плоскости в косоугольной системе координат определяется так. Проводим MP||Y`Y до пересечения с осью X`X в точке P и MQ||X`X до пересечения с осью Y`Y в точке Q, см. рисунок.

2. Расстояние между двумя точками прямой, плоскости и в пространстве.

Всякой паре точек, например, А и В на координатной прямой соответствует пара чисел х1 и х2. Найти расстояние между точками можно по формуле: р(А,В)=sqrt(xb-xa)

  Расстояние между двумя точками 

где   и   радиус-векторы точек   и  .

     В координатах:

     на прямой   

     на плоскости   

     в пространстве   

3. Деление отрезка в заданном отношении

Если точка М(x; y) лежит на прямой, проходящей через две данные точки  ( ,  ) и  ( ,  ), и дано отношение  , в котором точка М делит отрезок  , то координаты точки М определяются по формулам

,  .

Если точка М является серединой отрезка  , то ее координаты определяются по формулам

,  .

4. Полярная система координат. Сферическая система координат.

Полярная система координат. Полярная система координат задается точкой О, которая называется полюсом, лучом Ор, который называется полярной осью и единичным вектором е, того же направления что и полярная ось. Если мы возьмем на плоскости точку М, не совпадающую с О. Ее положение определяется двумя числами: ее расстоянием до r от полюса О и углом фи, который образован отрезком ОМ с полярной осью(Ор)(отсчет углов ведется по направлению противоположенному движению часовой стрелки.).

Числа rи фи- называются полярными координатами точки М. r- полярный радиус, фи- полярный угол.Чтобы получить все точки плоскости, достаточно ограничить полярный угол промежутком

Для введения сферической системы координат в пространстве выбирается плоскость (основная плоскость) и на ней задается полярная 1система координат с полюсом   (начало сферической системы координат) и полярной осью  . Через точку   перпендикулярно основной плоскости проведем ось   (ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси   происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки  , не лежащей на оси аппликат, характеризуется расстоянием   до начала координат, полярным углом   точки   - ортогональной проекции точки   на основную плоскость, и углом   между вектором   и положительным направлением оси аппликат. Таким образом, сферические координаты точки   - это упорядоченная тройка чисел   – радиус  , долгота   и широта  . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом   и широтой   для положительной части оси   и   для отрицательной ее части. Начало координат задается нулевым значением радиуса  . Иногда вместо угла   широтой называют угол  , принимающий значения 

Со сферической системой координат   можно связать прямоугольную систему координат   (рис.2.36,б), у которой начало и базисные векторы   совпадают с началом сферической системы координат и единичными векторами на полярной оси   и оси 5аппликат   соответственно, а базисный вектор   выбирается так, чтобы тройка   была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат (связанную с данной прямоугольной).