1. Матрицы и операции над ними

1) Система mn элементов a_ijнекоторого множества расположенных в виде прямоугольной таблицы из m строк и n столбцов называется матрицей размерности m×n.

Матрица строка (А=(a_ij)_1×n) Матрица столбец (A=(a_ij)_m×1)

2) Нулевая матрица (все элементы которой являются нулями)

3) Матрица А^Т называется транспонированной по отношению к любой матрице А, если её столбцами являются соответствующие строки матрицы А. (переход от А к А^Т называется транспонированием)

4) Квадратная матрица (если число её строк равно числу столбцов)

• Диагональная квадратная матрица (если все элементы вне главной диагонали равны нулю)

• Единичная матрица (все элементы главной диагонали равны 1, обозначается Е)

• Симметричная квадратная матрица (если выполняется равенство А^Т=А)

• Треугольная квадратная матрица (Если все элементы расположены по одну (в любую) сторону от главной диагонали равны нулю)

Операции над матрицами

1. Умножение матрицы на число

2. Сложение матриц

3. Умножение матриц (произведение двух матриц существует, если число столбцов первой матрицы равно числу строк второй (А_m×k * B_k×n = C_m×n)

2. Определите первого, второго и третьего порядка

Каждой квадратной матрице А ставится в соответствие единственное число, которое называется определителем (детерминантом) этой матрицы.

1. Определители первого прядка

|A|=|a₁₁|=a₁₁

2. Второго порядка

3. Третьего порядка

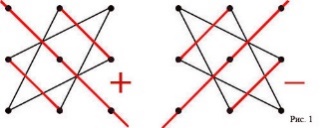
3. Миноры и алгебраические дополнения элементов. Определители n-го порядка.

• Минором элемента M_ijэлемента а_ijм. А n-го порядка (n≥2) называется определитель n-1-го порядка полученный из элементов матрицы А путем вычеркивания i-той строки и j-ого столбца, т.е. строки и столбца на пересечении которых стоит элемент a_ij.

• Алгебраическое дополнениеA_ijэлемента a_ijквадратной матрицы А n-го порядка (n≥2) – число определенное равенством: A_ij=(-1)^i+j * M_ij

• Определитель квадратной матрицы n-го порядка (n≥2) называется число |A|, определенное равенством: |A|= a₁₁A₁₁ + a₁₂A_{12 + …} + a_1nA_1n(Лаплас)

4. Свойства определителей

1. Определитель не меняется при транспонировании.

2. Определитель изменит свой знак, если поменять любые две строки.

3. Определитель n-го порядка равен сумме произведений элементов любой строки на соответствующие им алгебраические дополнения.

4. Определитель у которого две строки одинаковые равен нулю.

5. Если все элементы какой-либо строки определителя равны нулю, то и определитель равен нулю.

6. Если все элементы какой-нибудь строки определителя умножить на одно и тоже число, то значение определителя умножится на это число.

7. Определитель у которого элементы двух строк соответственно пропорциональны равен нулю.

8. Пусть каждый элемент i-ой строки определителя есть сумма двух слагаемых: a_ij=b_j+c_j (j=1, … ,n)

тогда заданный определитель равен сумме двух определителей: у одного из них i-ая строка состоит из элементов b_j, а у другого – из элементов c_j; все остальные строки этих двух определителей , кроме i-ой, имеют такие же элементы, как и исходный определитель.

9. Определитель не изменится, если к элементам какой-нибудь строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

10. Сумма произведений элементов какой-нибудь строки определителя на алгебраическое дополнение соответствующих элементов другой строки равна нулю, т.е. a_i1A_j1 + a_i2A_j2 + …+ a_inA_jn = 0