Ответы к экзамену по Математике:

1)Числовые ряды. Сходимость и сумма ряда.

Ответ: Бесконечным числовым рядом называется выражение: u₁+u₂+...+u_n+... , (1) содержащее неограниченное число членов, где: u₁ , u₂ , u₃ , ... , u_n , ... - бесконечная числовая последовательность; u_n называется общим членом ряда. Для составления ряда нужно знать закон образования общего члена. Например, если u_n = 2*n+1, то ряд имеет вид: 3, 5, 7, 9, ..., 501, 503, ..., n*2+1. Если u_n = (-1)ⁿ, то ряд имеет вид: -1, +1, -1, +1, ..., -1, +1, ..., (-1)ⁿ. Сумма первых n членов ряда обозначается символом S_n и называется частичной суммой этого ряда. Таким образом: S_n = u₁ + u₂ + ... + u_n. или, короче, Определение: Ряд называется сходящимся, если сумма первых его n членов при n®Ґ стремится к конечному пределу S, называемому суммой ряда. Если ряд (1) сходится, т.е. имеет сумму S, то пишут: S = u₁ + u₂ + ... + u_n + ... Если же при n®Ґ сумма Sn не имеет предела или то ряд (1) называется расходящимся и не имеет суммы. Типичным примером сходящегося ряда может служить ряд, полученный из бесконечно убывающей геометрической прогрессии: a + aq + aq² + aq³ + ... + aq^n-1 + ..., (2) где: -1 < q < 1. Действительно, для этого ряда Sn = a + aq + aq² + aq³ + ... + aq^n-1 = . При n®Ґ qⁿ®0 (так как | q |<1), поэтому и ряд (2) будет сходящимся. Таким образом можно написать = a + aq + aq² + aq³ + ... + aq^n-1 + ... . Если q = 1, то ряд (2) имеет вид: a + a + a + a + ... + a + ... . (3). Сумма S_n первых его n членов, равная na, по абсолютной величине неограниченно возрастает при неограниченном возрастании числа n. Таким образом, ряд (3) - расходящийся. Если q = -1, то ряд (2) примет вид: a - a + a - a + a - a +... +(-1)^n-1 a + ... . (4). Ясно, что для этого ряда: S_2n=0 , S_2n-1=a. т.е.сумма четного числа первых 2n членов ряда (4) стремится к нулю, а сумма нечетного числа первых 2n-1 его членов стремится к a. Отсюда следует, что ряд (4) расходится, так как в сходящемся ряде как S_2n так и S_2n-1 стремятся к одному и тому же пределу S. Ясно, что если | q |>1, то ряд (2) является также расходящимся.

2)Необходимый признак сходимости ряда.

Ответ: Теорема: Пусть числовой ряд: u₁+u₂+...+u_n+... , (1) сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член u_n стремится к нулю. Доказательство. Из условия теоремы имеем: , . Так как S_n - S_n-1 = u_n то . Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство а он, однако не является сходящимся. Так гармонический ряд: для которого расходится. Но согласно доказанному необходимому признаку сходимости ряда, если: ,то ряд (1) расходится. В самом деле, если бы он сходился, то равнялся бы нулю. Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы S_n, сделать заключение о расходимости того или иного ряда. Например, ряд: расходится, так как: .

3)Сравнение рядов с положительными членами.

Ответ:

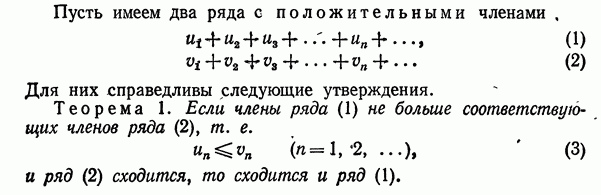
4)Признак Даламбера.

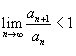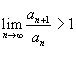Ответ: Признак Даламбера: Пусть − ряд с положительными членами. Тогда справедливы следующие свойства: 1)Если , то ряд сходится; 2)Если , то ряд расходится; 3)Если 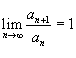, то ряд может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.

5)Признак Коши.

Ответ: Радикальный признак Коши: Снова рассмотрим ряд с положительными членами. Согласно признаку Коши: 1)Если , то ряд сходится; 2)Если , то ряд расходится; 3)Если , то вопрос о сходимости ряда , также как для признака Даламбера, остается открытым.

6)Интегральный признак сходимости ряда.

Ответ: Ряд вида: называется положительным, если все его члены неотрицательные Для определения сходимости в литературе собраны правила которые позволяют это быстро определить. Рассмотрим по очереди признаки сходимости числовых рядов Признак сравнения: Рассмотрим два ряда с положительными членами: , . Признак сравнения

Рассмотрим два ряда с положительными членами: 1)Если члены ряда не больше соответствующих членов сходящегося ряда ( ) то ряд сходится. Если каждый член ряда больше (или ровный) соответствующего члена росходящегося ряда то ряд разбегается.

Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд сходится, если сходится несобственный интеграл 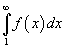, и расходится, если .
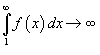