12. Оценка достоверности разности между средними арифметическими двух выборочных совокупностей с помощью нормативного распределения (1) и критерия р.

При сравнении средних арифметических двух генеральных со­вокупностей любая разность между ними будет достоверна. Поэтому необходимо установить достоверность разности между средними двух групп. Корреля́ция (от лат. correlatio — соотношение, взаимосвязь— статистическая взаимосвязь двух или нескольких случайных величин.

При этом изменения значений одной или нескольких из этих величин сопутствуют изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение , либо коэффициент корреляции (или ). В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.

Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков.

Когда повышение уровня одной переменной сопровождается повышением уровня другой, то речь идет о положительной корреляции. Если же рост одной переменной происходит при снижении уровня другой, то говорят об отрицательной корреляции. При отсутствии связи переменных мы имеем дело с нулевой корреляцией. Корреляционный анализ Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными.

Показатели корреляции Параметрические показатели корреляции Ковариация

Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация определяется как математическое ожидание произведения отклонений случайных величин.

,

где  — математическое ожидание.

Свойства ковариации:

• Ковариация двух независимых случайных величин и равна нулю.

• Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий: .

• Ковариация имеет размерность, равную произведению размерности случайных величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа.

Линейный коэффициент корреляции

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона. Коэффициент корреляции рассчитывается по формуле:

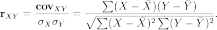
где ,  — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы.

Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где  — коэффициент регрессии,  — среднеквадратическое отклонение соответствующего факторного признака.