11.Теория ошибок (формула Гаусса нормального распределения вариант, ошибка среднего арифметического, доверительный интервал выборочной средней и доверительная вероятность). Коэффициенты Стьюдента.

В теории случайных ошибок измерений важное значение

имеет нормальный закон распределения или функция Гаусса. Он

справедлив, когда действуют сразу несколько источников оши-бок, и ни один из них не доминирует; при этом каждый источ-ник вносит лишь малую долю в общую ошибку. Нормальный

закон распределения вероятности случайных ошибок описыва-ется формулой Гаусса:

где x — случайная величина измерения; x0— ее истинное зна-чение; чаще всего неизвестно; ¾

2— дисперсия распределения; e = 2; 71928 — фундаментальная математическая постоянная.

В математической статистике показывается, что в качестве истинного значения x0 можно использовать среднее арифмети-ческое из n измерений: где x

i — значение i-го измерения случайной величины x. Чем больше проведено испытаний (n), тем лучше выполняется это утверждение. Форма кривых Гаусса устанавливает, насколько часто долж-ны появляться ошибки той или иной величины. Видно, что чем больше дисперсия случайной величины ¾, тем шире кривая и ниже ее пик. Таким образом, для большой дис-персии вероятность, пропорциональная ½(x), слабо спадает при отклонении от истинного значения x0 . Наоборот, для малой дис-персии вероятность получить такое же измерение мала. Значе-ние ¾ характеризует качество методики измерения: чем меньше дисперсия, тем лучше методика. В реальном эксперименте мы имеем конечное число испыта-ний n. Поэтому, как и для среднего арифметического, вводится величина, характеризующая среднее отклонение случайной ве-личины x от x; она называется средне-квадратичным отклоне-нием (ошибкой): Оказывается, что при сколь угодно большом числе измере-ний, средне-квадратичная ошибка стремится к дисперсии: Доверительный интервал. Доверительный интервал - интервал значений от ̄х -∆х до ̄х +∆х, в который попадает истинное значение величины. Так как ∆х является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α.

Эта вероятность называется доверительной.

Существует статистическая оценка измеряемой величины, в соответствии с которой средняя квадратичная ошибка равна средней квадратичной ошибке среднего арифметического(Sх̄).

Она рассчитывается:

- результат итого измерения

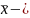среднее арифметическое полученных значений

n-число измерений

Для нахождения доверительного интервала и вероятности при небольшом числе измерений используется распределение вероятностей Стьюдента. Это распределение вероятностей случайной величины.

tαn-коэффициент Стьюдента. Он дает значение доверительного интервала ∆х в долях средней квадратичной ошибки среднего арифметического.

Распределение вероятностей этой величины не зависит от дисперсии измерений (α ²), а зависит от числа опытов (n). С увеличением числа опытов распределения Стьюдента стремится к распределению Рауса. Поскольку среднее арифметическое x имеет меньшую ошиб-ку, то надо решить задачу: насколько оно близко к истинному x0 при n измерениях. Подобно случаю нормального распределения, справедливого при n ! 1, составим отношение: Числа tg;n называются коэффициентами Стьюдента, они

зависят от выбранной (или искомой) надежности ® и числа из-мерений n. Таким образом, коэффициенты t®;n играют такую же роль, как и " ³ ¢x ¾ , но для конечного числа измерений. Для малого числа измерений использование нормального распреде-ления (5) даст ошибку, и тем большую, чем меньше n. Значит надо использовать более точное распределение вероятностей, за-висящее от n.