5.Арифметические свойства[править | править вики-текст]
Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.
Однородность. Константу можно выносить из-под знака предела.
Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.
Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
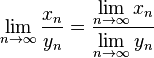
6. Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Теорема 1 (о связи предела с бесконечно малой функцией). Для того, чтобы существовал
lim x → x0 f(x) = A,
необходимо и достаточно, чтобы функцию f(x) можно было представить в виде
f(x) = A + α(x),
где α(x) — бесконечно малая функция при x → x0.
7. Функция α(x), определенная в точке (x 0), называется бесконечно малой функцией при x → x0, если
lim x → x0 α(x) = 0.
8. Теоремы:
1)Предел
суммы двух функций равен сумме их
пределов:
.
Доказательство:
Пусть 
,
.
Тогда по теореме о связи функции, её
предела и бесконечно малой функции
можно записать: 
и 
.
Следовательно, 
,
где 
-
бесконечно малая функция (по свойству
бесконечно малых функций). Тогда по
теореме о связи функции, её предела и
бесконечно малой функции можно
записать 
, или
.
2)Предел
произведения двух функций равен
произведению их пределов:
.
Доказательство:
Пусть
,
.
Тогда
и 
.
Следовательно
,
.
Выражения
в скобках, по свойствам бесконечно малых
функций, - бесконечно малая функция.
Тогда 
,
т.е.
.
2)Предел
частного двух функций равен пределу
делимого, деленного на предел делителя,
если предел делителя не равен:
.
Доказательство:
Пусть
,
.
Тогда 
и 
.
Тогда 
. По
свойствам бесконечно малых функций,
второе слагаемое – бесконечно малая
функция.
Поэтому 
,
т.е. 
9. Теорема о пределе частного двух функций.
Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен: .
Доказательство:
Пусть , . Тогда и . Тогда . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.
Поэтому , т.е.
10. Теорема о пределе промежуточной функции.
Если
функция
|
такая,
что 
для
всех 
в
некоторой окрестности точки 
,
причем функции 
и 
имеют
одинаковый предел при 
,
то существует предел функции
при
,
равный этому же значению, то есть
Доказательство
Из
неравенства
получаем
неравенство 
.
Тогда верно неравенство 
.
Условие 
позволяет
предположить, что для любого 
существует
окрестность 
,
в которой верны неравенства 
и 
.
Из изложенной выше оценки максимумом
следует, что 
при 
,
что удовлетворяет определению предела,
то есть 
11. Теорема о пределе положительной (отрицательной) фунцкии. Предел функции по Коши
Значение 
называется пределом (предельным
значением)
функции 
в
точке 
,
если для любого наперёд взятого
положительного числа 
найдётся
отвечающее ему положительное число 
такое,
что для всех аргументов
,
удовлетворяющих условию 
,
выполняется неравенство 
.[1]
12.Первый замечательный предел
Доказательство
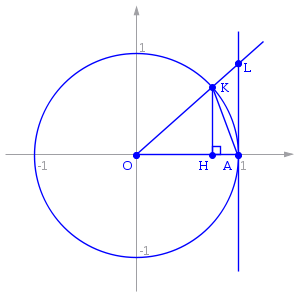
Рассмотрим односторонние
пределы 
и 
и
докажем, что они равны 1.
Пусть 
.
Отложим этот угол на единичной окружности
(
).
Точка K —
точка пересечения луча с окружностью,
а точка L —
с касательной к единичной окружности
в точке 
.
Точка H —
проекция точки K на
ось OX.
Очевидно, что:
(1)
(где 
—
площадь сектора 
)
(из 
: 
)
Подставляя в (1), получим:
Так
как при 
:
Умножаем
на 
:
Перейдём к пределу:
Найдём левый односторонний предел:
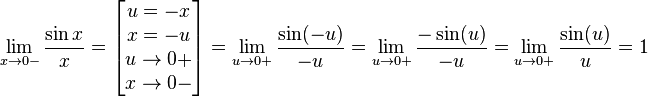
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
13.Второй замечательный предел
или 
Доказательство второго замечательного предела:
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что 
.
Рассмотрим два случая:
1.
Пусть 
.
Каждое значение x заключено между двумя
положительными целыми числами: 
,
где 
—
это целая часть x.
Отсюда
следует: 
,
поэтому
.
Если
,
то 
.
Поэтому, согласно пределу 
,
имеем:
.
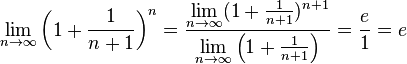
По
признаку (о пределе промежуточной
функции) существования пределов 
.
2.
Пусть 
.
Сделаем подстановку 
,
тогда
.
Из
двух этих случаев вытекает, что
для
вещественного x. 
14.Различные формы записи 2 замечательного предела
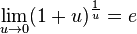
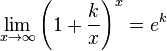
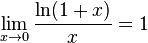
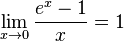
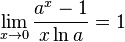для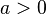 
, 
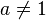
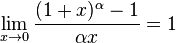
15.Различные определения непрерывности функции
Функция
называется непрерывной в точке
если:
1)Функция f (x) определена в точке x = a;
2)Предел
существует
3)Выполняется
равенство
1)Определение непрерывности по Коши
Рассмотрим
функцию f
(x),
которая отображает множество действительных
чисел
на
другое подмножество B
действительных чисел. Говорят, что
функция f
(x)
является непрерывной
в точке
,если для любого числа
существует число
,
такое, что для всех
удовлетворяющих соотношению
выполняется неравенство
2)Определение непрерывности в терминах приращений аргумента и функции Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке x = a, если справедливо равенство
где
16.Односторонние пределы,связь односторонних пределов с пределами функции.
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
1)Число
называется правосторонним пределом
функции
при
стремящемся к
если
2)Число называется левосторонним пределом функции при стремящемся к если
Для
существования обычного (двустороннего)
предела функции
в
точке a
необходимо и достаточно равенство между
собой односторонних пределов:
17.Классификация точек разрыва. В этом случае точка хо называется точкой разрыва для ф-ции у=f(х). Существуют три вида точек разрыва. 1)если существует предел limxхоf(x)=a, но он не равен значению ф-ции в точке хо, тогда точка хо – точка устранимого разрыва. (см.рис.2). 2)если существует предел ф-ции f(x) при х стремящемся от хо справа,т.е. limxхо+0f(x)=f(xo+0). Существует предел ф-ции f(x) при ххо слева, т.е. limxхо-0f(x)=f(xo-0), но они не равны между собой f(xo+0)≠f(xo-0), то хо-точка разрыва 1-го рода (точка скачка). (см.рис.3). Разность f(xo+0)-f(xo-0)-величина скачка в точке хо, т.е. всегда от правостороннего отнимается левосторонний. 3)если хотя бы один из односторонних пределов в точке хо не сущ. или равен ∞, то точка хо называется точкой разрыва второго рода. (см.рис.4.). limxхо-0f(x)=a; limxхо+0f(x)=+∞. 3у=х/|х|, х≠0 limх0+ х/|х|= limх0 х/х=1 и limх0- х/|х|= limх0 х/-х=-1 => по определению, что точка х=0 – точка разрыва 1-го рода.
18.Свойства функций, непрерывных на отрезке.
Ф-ция у=f(х) назыв.непрерывной на интервале (а;b) если она непрерывна в каждой точке этого интервала. Опр. limxa+0f(x)=f(a), то ф-ция f(х) называется непрерывной в точке а справа.. limxb-0f(x)=f(b), то ф-ция f(х) называется непрерывной в точке b слева. Опр: ф-ция у=f(х) назыв. непр.на отрезке [a;b] если она непрерывна в каждой точке интервала (а;b), непрерывна справа в точке а и непрерывна слева в точке b. Если в какой-то точке хо для ф-ции у=f(х) не выполняется хотя бы одно условие непрерывности, то ф-ция у=f(х) разрывна в точке
19.Производная.Геометрический смысл производной.
Геометрический смысл производной состоит в следующем: производная вычисленная в данной точке, есть tg угла наклона касательной проведенной в данной точке, при этом угол отсчитывается от оси х до касательной.
20.Теорема о связи непрерывности и дифференцировании функции.
Если
функция 
дифференцируема
в точке 
,
то она непрерывна в
этой точке.
Доказательство. Так
как функция 
дифференцируема в
точке
,
то существует конечный предел 
.
Тогда по теореме о связибесконечно
малой с
функцией, имеющей конечный предел, будем
иметь
,
где 
бесконечно
малая величина при 
.
Откуда
.
Переходя
в этой формуле к пределу при
,
получим по свойствам бесконечно малых,
что 
.
Следовательно, по одному из определений непрерывности функция в точке является непрерывной.
Обратная теорема, вообще говоря, неверна, т.е. функция может быть непрерывной в данной точке, но не быть дифференцируемой в этой точке.
В
качестве примера исследуем функцию 
в
точке 
,
которая непрерывна в точке
(впрочем,
как и во всех других точках числовой
прямой). В этой точке ее левосторонний
и правосторонний
пределы равны
нулю, что совпадает со значением самой
функции в точке 
.
По определению
Таким
образом, функция
в
точке 
имеет
конечные, но не равные друг другу
односторонние производные (левая
равна 
,
а правая равна 
).
Поэтому она не имеет производной в этой
точке и не является в ней дифференцируемой.
Вопрос 21. Производные основных элементарных функций.
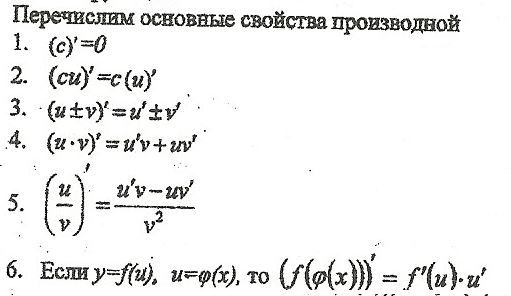
Вопрос 22. Теоремы о вынесении константы за знак производной и о производной суммы двух функций.
Константу можно вынести за знак производной, то есть
Теорема о производной суммы двух функций.
Вопрос 23. Теорема о производной произведения.
Вопрос 24. Теорема о производной частного.
37.
Экстремумы- это минимум или максимум функции.
Необходимое условие:
Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.
Достаточное условие:
Если непрерывная функция F(x) содержащая критическую точку X0 дифференцируема на интервале, содержит эту точку, меняет знак производной с — на +, то в этой точке локальный минимум, а если наоборот, то локальный максимум.
38.
Точки перегиба определяют интервал выгнутости и вогнутости кривой. Кривая вогнута на интервале АВ, если F”(x)>0 для b>x>0 и выгнута F”(x)<0 для b>x>a
Точки перегиба являются точками экстремума для 1-ой производной.
Необходимые условия существования точки перегиба являются:
F”(x)=0
F”(x)=бесконечности
F”(x)=не существует, но сама функция в точке X=X0 определена.
Говорят, что кривая выгнута на отрезке AB, если касательная каждой точки этого отрезка расположена выше графика функции, и наоборот если вогнута. На выпуклость и вогнутость оказывает влияние знак второй производной.
39.
Прямая на плоскости называется асимптотой графика функции, если растояние от текущей точки графика,до этой прямой уменьшается по мере удаления от начала координат.
Прямая x=a будет являтся вертикальной асимптотой, если точка x=a будет точкой разрыва 2-го рода
для нахождения ноклонной асимптоты нужно определить коэфициенты k и b уравнения y=kx+b
В случае, если k=0, то наклонная асимптота превращается в горизонтальную.
40.
Комплексным числом называют выражение вида z=x+iy, где xy- действительный числа, а i мнимая еденица.
Операции над комплексными числами:
сложени, вычитание, умножение, деление, возведение в степень, извлечение корня.