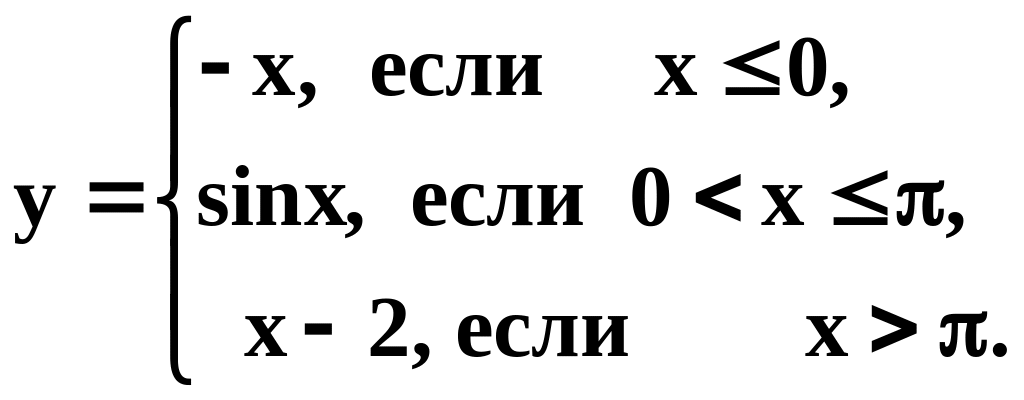- •Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Вариант № 11
- •Вариант № 12
- •Вариант № 13
- •Вариант № 14
- •Вариант № 15
- •Вариант № 16
- •Вариант № 17
- •Вариант № 18
- •Вариант № 20
- •Вариант № 21
- •Вариант № 22
- •Вариант № 23
- •Вариант № 24
- •Вариант № 25
- •Вариант № 26
- •Вариант № 27
- •Вариант № 28
- •Вариант № 29
- •Вариант № 30
Вариант № 9
Вычислить пределы числовых последовательностей:
1)
![]() ;
3)
;
3)
![]() ;
;
2)
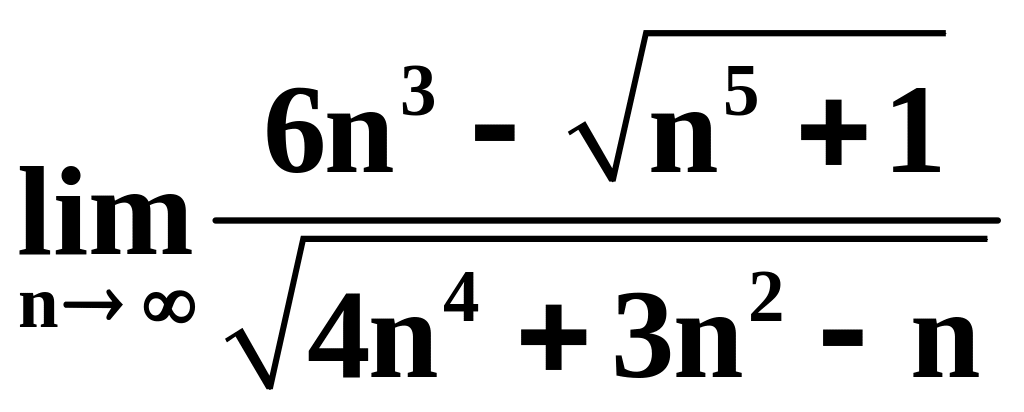 ;
4)
;
4)
![]() .
.
Замечание. Воспользоваться равенством:12+22+32+…+n2=n(n+1)(2n+1)/6.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
![]() ;
8)
;
8)
![]() ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
![]() ;
10)
;
10)
![]() ;
;
5)
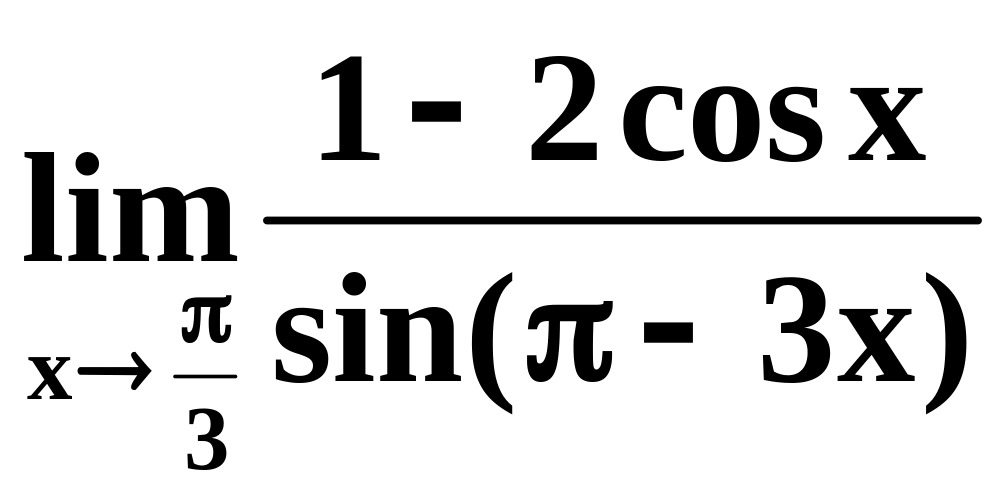 ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
;
12)
![]() .
.
3. По
эскизу графика описать поведение функции
на языке пределов в точках
и
![]() и при стремлении аргумента функции к
.
и при стремлении аргумента функции к
.
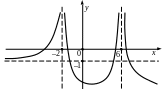
4. Построить график функции , если известно, что
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
.
;
.
Дать каждому из пределов определение по Коши (используя неравенства для задания - и -окрестностей).
5. Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1) ;
2)
;
2)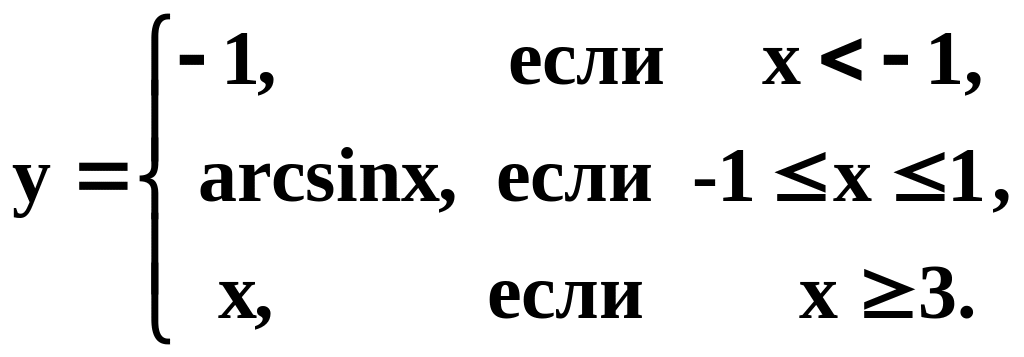
Вариант № 10
Вычислить пределы числовых последовательностей:
1)![]() ;
3)
;
3)
![]() ;
;
2)
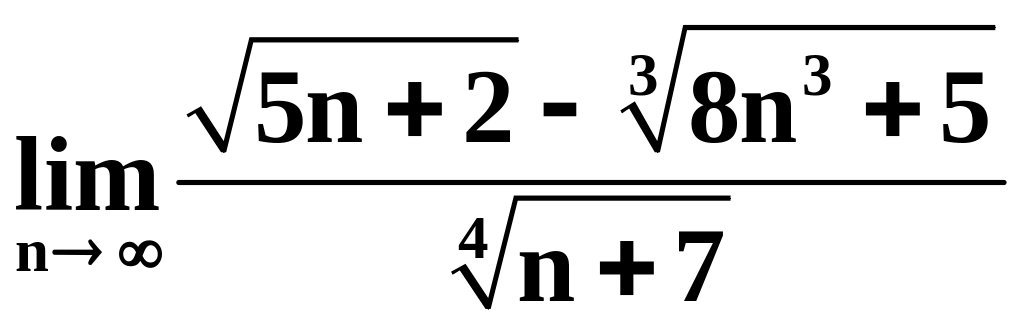 ;
4)
;
4)
![]() .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
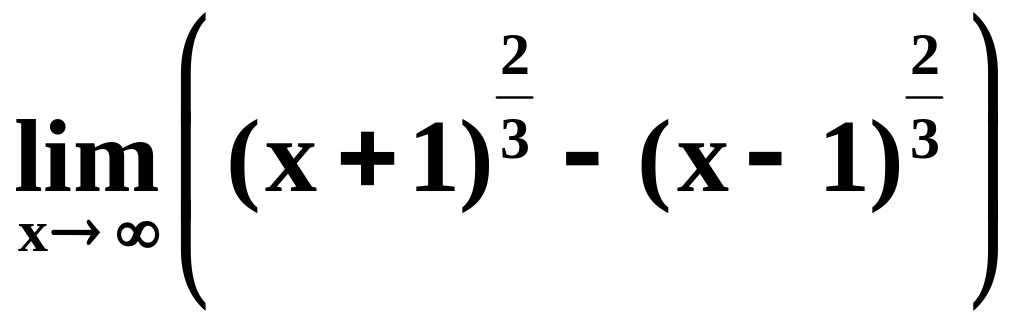 ;
;
2)
![]() ;
8)
;
8)
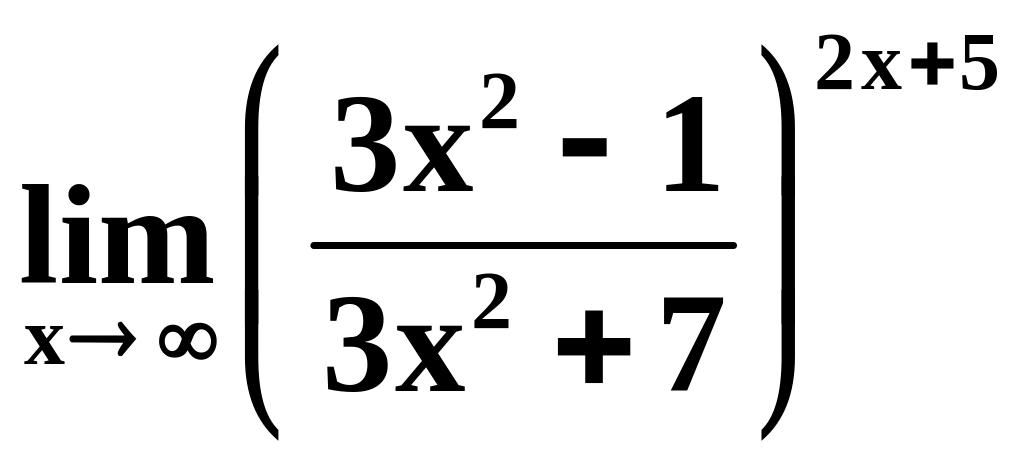 ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
 ;
10)
;
10)
![]() ;
;
5)
![]() ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
;
12)
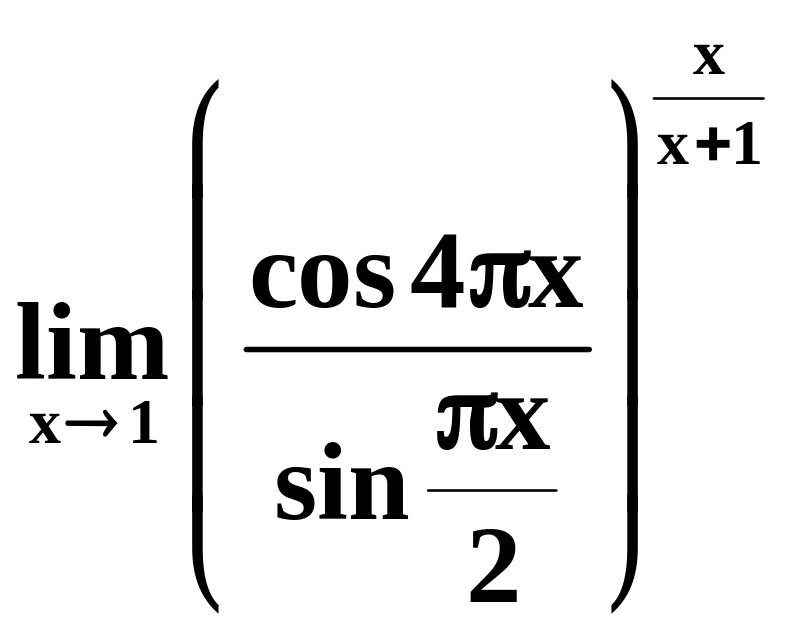 .
.
3. По эскизу графика описать поведение функции на языке пределов в точках и и при стремлении аргумента функции к .
x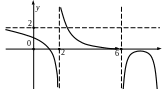
4. Построить график функции , если известно, что
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
;
.
,
;
.
Дать каждому из пределов определение по Коши (используя неравенства для задания - и -окрестностей).
5. Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1)
![]() ;
2)
;
2)
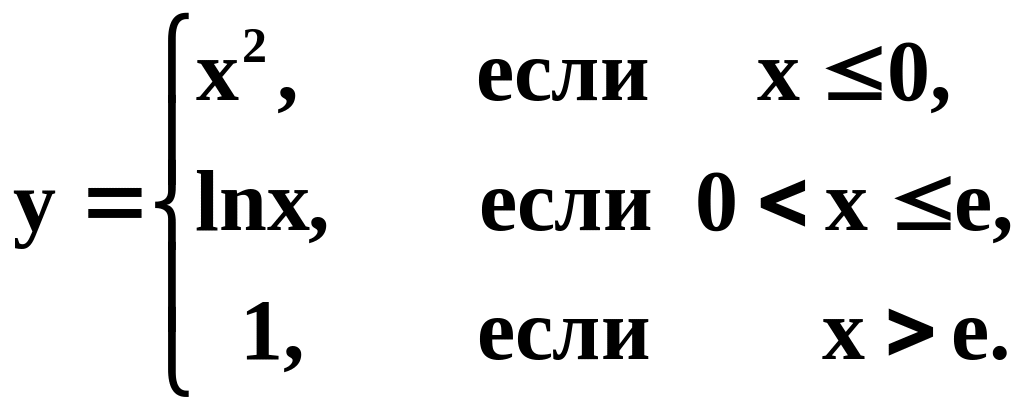
Вариант № 11
Вычислить пределы числовых последовательностей:
1)
![]() ;
3)
;
3)
![]() ;
;
2)
![]() ;
4)
;
4)
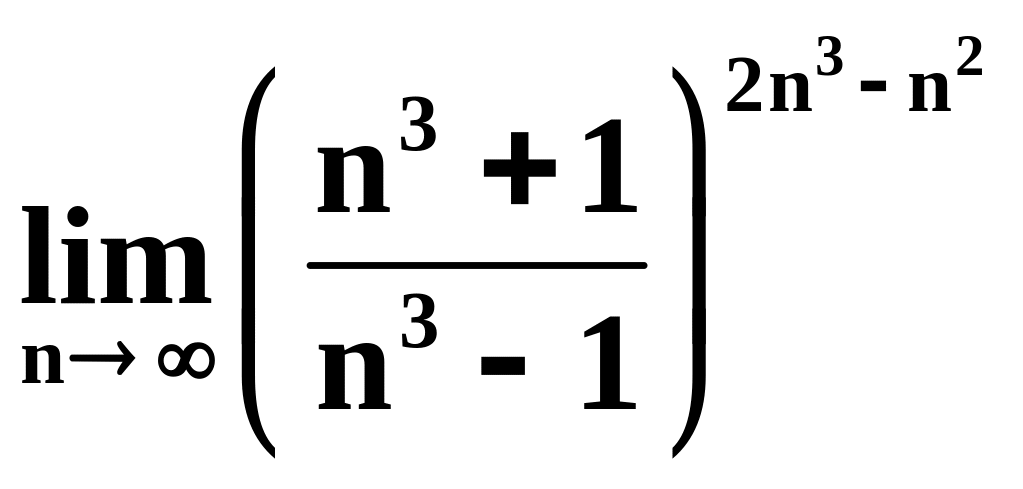 .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
;
8)
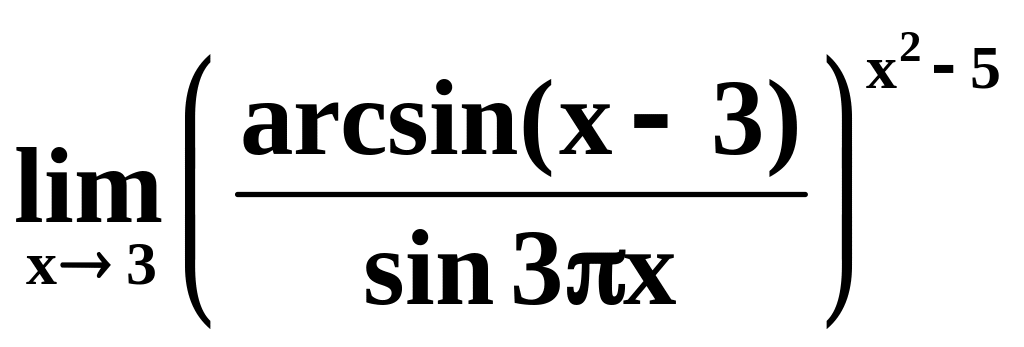 ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
![]() ;
10)
;
10)
![]() ;
;
5)
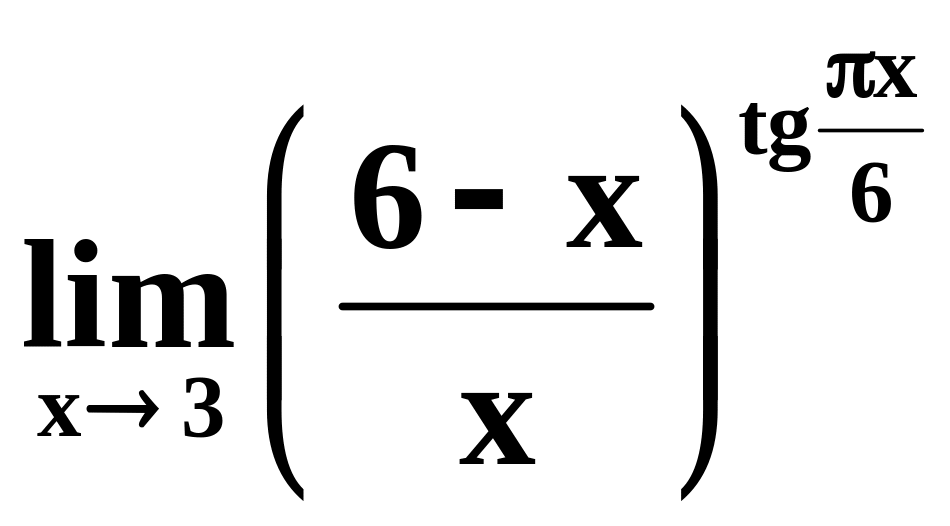 ;
11)
;
11)
![]() ;
;
6)
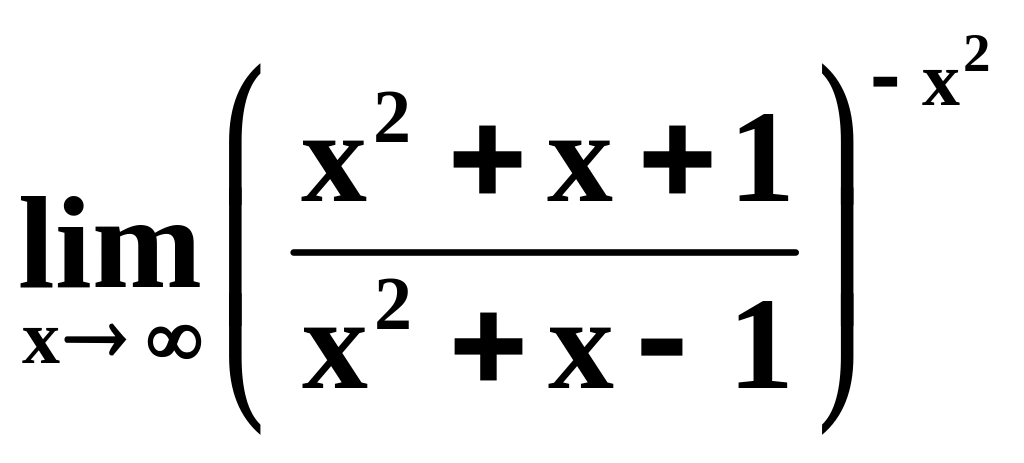 ;
12)
;
12)
![]() .
.
3. По
эскизу графика описать поведение функции
на языке пределов в точках
![]() и
и при стремлении аргумента функции к
.
и
и при стремлении аргумента функции к
.
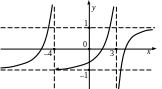
4. Построить график функции , если известно, что
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
; ![]() .
.
Дать каждому из пределов определение по Коши (используя неравенства для задания - и -окрестностей).
5. Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1)
![]() ;
2)
;
2)
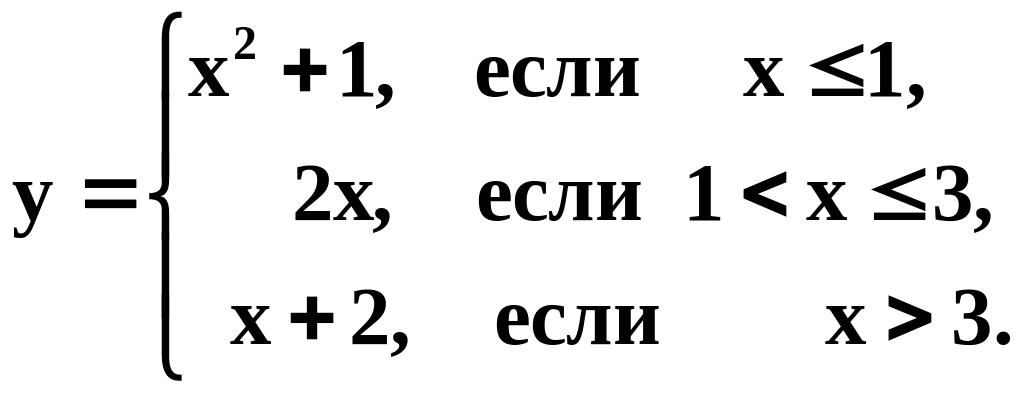
Вариант № 12
Вычислить пределы числовых последовательностей:
1)
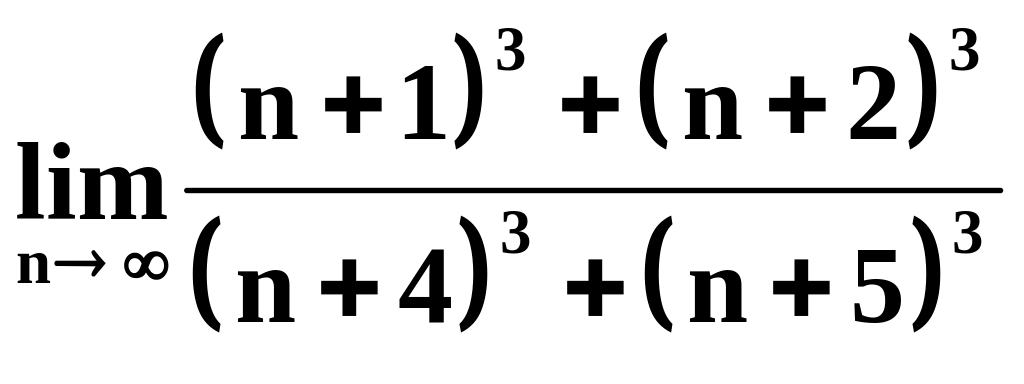 ;
3)
;
3)
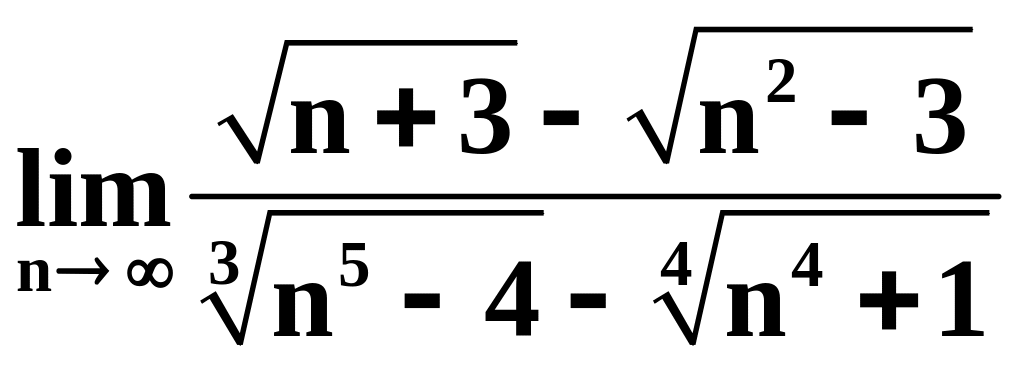 ;
;
2)
![]() ;
4)
;
4)
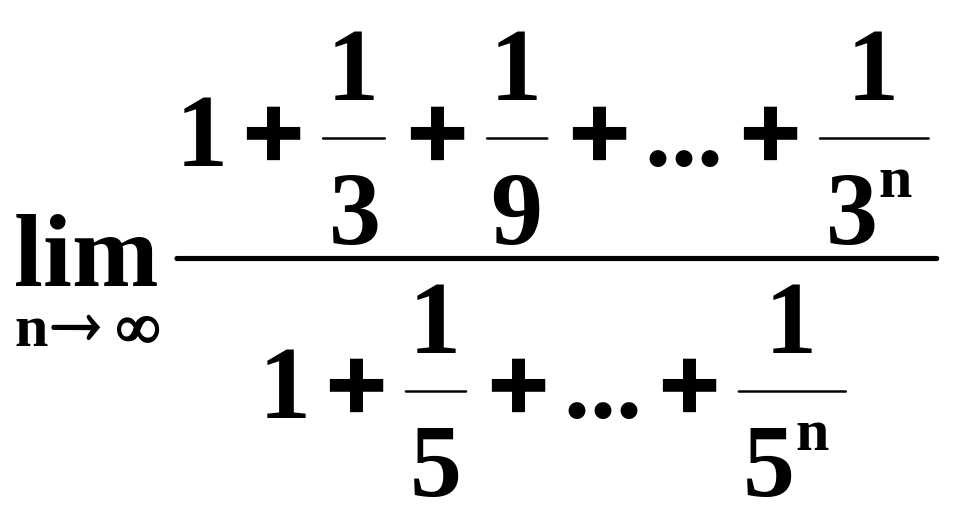 .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
![]() ;
8)
;
8)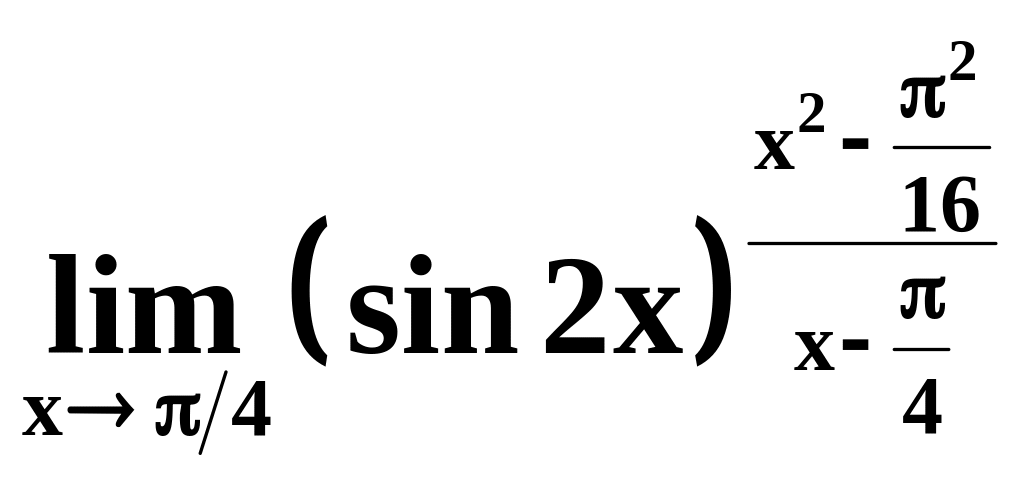 ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
![]() ;
10)
;
10)
![]() ;
;
5)
![]() ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
;
12)
![]() .
.
3. По эскизу графика описать поведение функции на языке пределов в точках и и при стремлении аргумента функции к .
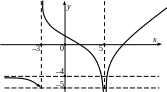
4. Построить график функции , если известно, что
, , ,
![]() ,
, ![]() ;
; ![]() .
.
Дать каждому из пределов определение по Коши (используя неравенства для задания - и -окрестностей).
5. Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1)
![]() ;
2)
;
2)