1111111111111111111111111111111111111111111111111111111111111

Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

где  - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы,  - сила действующая на частицу. Сопоставим с классическим уравнением

Мы приходим к выводу, что релятивистский импульс частицы равен

(6.7)

Релятивистская масса.

Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.

(6.8)

Энергия в релятивистской динамике.

Для энергии частицы в теории относительности получается выражение:

(6.9)

Из (2.3) следует, что покоящаяся частица обладает энергией

(6.10)

Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

(6.11)

Приняв во внимание, что  , выражение для полной энергии частицы можно написать в виде

(6.12)

Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела   сопровождается изменением массы тела

и, наоборот, всякое изменение массы   сопровождается изменениемэнергии  . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.

Энергия релятивистской частицы

Полная энергия релятивистской частицы  . Полная энергия включает в себя все виды энергии: механическую, тепловую, химическую, ядерную и т.д. Энергия частицы при v=0, т.е.  называется энергией покоя. Это -- максимальная энергия, заключенная в покоящейся в данной системе отсчета частице (теле); она включает в себя энергию внутриатомных и внутриядерных взаимодействий. Согласно определению, кинетическая энергия частицы (энергия движения) будет равна разности полной энергии и энергии покоя Из формулы следует, что ни одна частица с массой, отличной от нуля, не может двигаться со световой скоростью ! И наоборот, безмассовые частицы (m=0) могут существовать, только двигаясь со скоростью света ! При малых скоростях (v << c)   и  , т.е. формула приводит к хорошо известному классическому выражению для кинетической энергии частицы. С другой стороны, полную энергию можно представить, как сумму энергии покоя и кинетической энергии частицы  . Можно энергию и  импульс  объединить в один общий 4-вектор энергии-- импульса       или   Последнюю формулу можно применять и для безмассовых частиц, к которым относятся фотоны. Для них формула дает: E = PC .

Динамические и статистические закономерности – два класса закономерностей, различающиеся характером лежащих в их основе связей и зависимостей. Динамические законы характеризуют поведение отдельного объекта или системы, включающей небольшое число элементов, и раскрывают необходимую связь между состояниями этого объекта или системы. Они дают возможность вполне определенно предсказать будущее состояние объекта, если известно его настоящее состояние.

К динамическим законам относятся законы, выражающие причинно-следственные связи, функциональные отношения и т.п. Таковы, например, законы классической механики и открытый в химии закон сохранения вещества. Динамические законы проявляют себя во всех областях действительности, на всех уровнях организации материи.

Представления о динамических закономерностях являются исторически первыми. Они сформировались под воздействием развития классической физики и прежде всего – классической механики. Механика исходит из изучения законов движения отдельных, индивидуализированных макротел. Основной задачей ее является определение траектории движения макротел под воздействием сил. Весьма существенно, что эта траектория определяется единственным образом. Логическая структура механики легла в основу характеристики динамических закономерностей. Соответственно, в качестве определяющей черты класса динамических закономерностей рассматривается строго однозначный характер всех без исключения связей и зависимостей, отображаемых в рамках соответствующих представлений и теорий.

Статистические (вероятностные) законы – это законы, выражающие некоторую тенденцию, сложившуюся в совокупности явлений во взаимодействии множества случайных факторов.

Они позволяют с высокой точностью делать прогностические выводы о поведении больших совокупностей объектов, но не достигающие такой точности при прогнозе поведения отдельных ее элементов.

111111111111111111111111111111111111111111111111

Статистический и термодинамический методы исследования

Молекулярная физика и термодинамика — разделы физики, в которых изучаются зависимости свойств тел от их строения, взаимодействия между частицами, из которых состоят тела, и характера движения частиц.

Для исследования физических свойств макроскопических систем, связанных с огромным числом содержащихся в них атомов и молекул, применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (или молекулярно-кинетический) и термодинамический.

Статистический метод — это метод исследования систем из большого числа частиц, оперирующий статистическимизакономерностями и средними (усредненными) значениями физических величин, характеризующих всю систему.

Этот метод лежит в основе молекулярной физики — раздела физики, изучающего строение и свойства вещества исходя из молекулярно- кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. В дальнейшем мы будем использовать термин "молекула" имея ввиду мельчайшую структурную единицу (элемент) данного вещества.

Термодинамический метод — это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом (например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц.

Этот метод лежит в основе термодинамики — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.

Макроскопическое состояние системы характеризуется ограниченным количеством термодинамических величин, называемых термодинамическими функциями. [1]

Макроскопическое состояние системы определено, если известны такие макроскопические параметры, как давление, температура, химический состав системы. [2]

Естественно, что макроскопическое состояние системы зависит от состояния отдельных составляющих эту систему частиц. Однако состояние каждой отдельной частицы в какой-либо момент времени не предсказуемо. [3]

Естественно, что макроскопическое состояние системы зависит от состояния отдельных составляющих эту систему частиц. Однако состояние каждой отдельной частицы в какой-либо момент времени непредсказуемо. [4]

Как известно, знание макроскопического состояния системы, определяемого давлением, объемом и температурой, не позволяет судить о положении в пространстве и скорости отдельных молекул. Поэтому с молекулярно-кинетической точки зрения данное макроскопическое состояние можно реализовать большим числом различных способов, поскольку состояние каждой молекулы определяется шестью параметрами ( три координаты положения и три составляющие скорости) и каждый из этих параметров изменяется непрерывно. При наличии N молекул состояние газа определяется, следовательно, 6N параметрами. Однако следует учитывать, что состояние газа зависит не от направления скоростей, а от кинетической энергии молекул и, кроме того, перестановка кинетических энергий молекул не изменит макроскопического состояния газа. Поэтому макроскопическое состояние коллектива N молекул, в сущности, зависит от меньшего числа параметров и может быть реализовано при помощи некоторого числа комплексий, характеризующих некоторое определенное распределение, при котором каждая различимая молекула имеет данную кинетическую энергию. Согласно представлению о молекулярном хаосе, все комплексий равновероятны. Очевидно, из двух заданных состояний то, которое может быть реализовано при помощи большего числа комплексий, имеет и большую вероятность. Число комплексий, позволяющих реализовать данное состояние, есть термодинамическая вероятность этого состояния или его статистический вес. Из этого определения следует, что термодинамическая вероятность отличается от математической, которая всегда меньше единицы. [5]

Число микроскопических состояний, соответствующее определенному макроскопическому состоянию системы, называется термодинамической вероятностью w этого макроскопического состояния. [6]

Число различных микроскопических состояний, соответствующее определенному макроскопическому состоянию системы, получило название термодинамической вероятности ( W) этого макроскопического состояния. Термодинамическая вероятность выражается большими числами и резко возрастает при переходе от твердого состояния тела к газообразному как менее упорядоченному. Этой величиной в статистической физике пользуются как мерой вероятности состояния. [7]

Наличие неполных равновесий позволяет ввести понятие о макроскопических состояниях системы. Например, это могут быть средние значения величин, характеризующих отдельные достаточно малые, но макроскопические части системы, каждую из которых можно считать находящейся в некотором своем частном равновесии. [8]

При возрастании числа микроскопических состояний Q, связанных с макроскопическим состоянием системы, энтропия увеличивается. [9]

Рассмотренные ион-дипольное и ион-ионное взаимодействия относятся к равновесным условиям, когдамакроскопическое состояние системы, характеризуемое термодинамическими функциями, не изменяется во времени. Однако равновесие в растворах электролитов всегда является динамическим, усредненным по времени и по объему. Частицы раствора ( ионы и диполи растворителя) все время совершают хаотические движения, которые осуществляются периодическими перескоками с одного места на другое. Но в среднем эти перемещения частиц скомпенсированы, так что направленного макроскопического перехода ионов и диполей в условиях равновесия не происходит. Если в растворе электролита наблюдаются ионные равновесия, то они также имеют динамический характер. [10]

Задача статистической физики состоит в исследовании связи между микро - и макроскопическими состояниями систем. [11]

Поскольку обрыв цепи является диффузионно-контролируемым процессом, Ct существенным образом зависит от макроскопического состояния системы. Как известно, вязкость большинства жидкостей при давлениях порядка нескольких тысяч атмосфер возрастает в несколько раз. [12]

В статистической физике, однако, каждому состоянию приписывается определенная вероятность, обусловленная макроскопическим состоянием системы. [13]

Отметим, что энтропия Гиббса является информационной энтропией классических и квантовых ансамблей, представляющих макроскопическое состояние системы многих частиц. Поскольку в квантовом определении энтропии Гиббса (1.3.6) величины wn ( n Q n) есть вероятности нахождения системы в квантовых состояниях п), то энтропия Гиббса для смешанных квантовых ансамблей также является информационной энтропией. [14]

121212121212121212121212121212

Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1) потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосудаабсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют форму упругих сфер илиэллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц^[1]. В рамках термодинамики идеальным называется газ, подчиняющийся термическому уравнению состояния Клапейрона — Менделеева^[2][3].

Модель широко применяется для решения задач термодинамики газов и задачаэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температурес большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Диракаили Бозе — Эйнштейна).

Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

• Диаметр молекулы 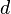  пренебрежимо мал по сравнению со средним расстоянием между ними (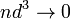 ) ^[9][10].

• Импульс передается только при соударениях, то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях.

• Суммарная энергия частиц газа постоянна, если отсутствует теплопередача и газ не совершает работы.

В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно полному импульсу, переданному при столкновении частиц со стенкой в единицу времени, внутренняя энергия — сумме энергий частиц газа.

По эквивалентной формулировке идеальный газ - такой газ, который одновременно подчиняется закону Бойля — Мариоттаи Гей-Люссака^[10], то есть:

где   — давление,   — абсолютная температура. Свойства идеального газа описываются уравнением Клапейрона — Менделеева

,

где   - универсальная газовая постоянная,   — масса,   — молярная масса.

или

где   — концентрация частиц,   — постоянная Больцмана.

Для любого идеального газа справедливо соотношение Майера:

где   — универсальная газовая постоянная,   — молярная теплоемкость при постоянном давлении,   — молярная теплоемкость при постоянном объёме.

. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).