Тема 5. Гидравлический расчет трубопроводов Расчет простых трубопроводов постоянного сечения

Простым называется трубопровод постоянного или переменного сечения, который не имеет ответвлений и в котором расход жидкости постоянный по длине (рис. 5.1).

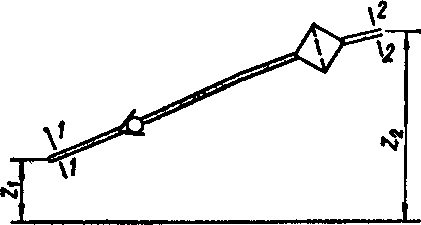
Рисунок 5.1 – Простой трубопровод постоянного сечения

Исходными для гидравлического расчета трубопровода являются:

1) уравнение Бернулли:

; (5.1)

2) уравнение неразрывности:

; (5.2)

3) зависимость для определения потерь напора на трение по длине (Дарси-Вейсбаха):

; (5.3)

4) зависимость для определения потерь напора в местных сопротивлениях (Ю. Вейсбаха):

. (5.4)

При расчете простых трубопроводов встречаются следующие типовые задачи.

Задача 1. Требуется определить расход жидкости при заданных геометрических размерах трубопровода ( , , ), отметках точек ( и ), давлениях ( и ) и местных сопротивлениях ( ).

Из уравнения Бернулли, которое вследствие постоянства скоростей по длине, принимает вид

, (5.5)

способом последовательных приближений находят:

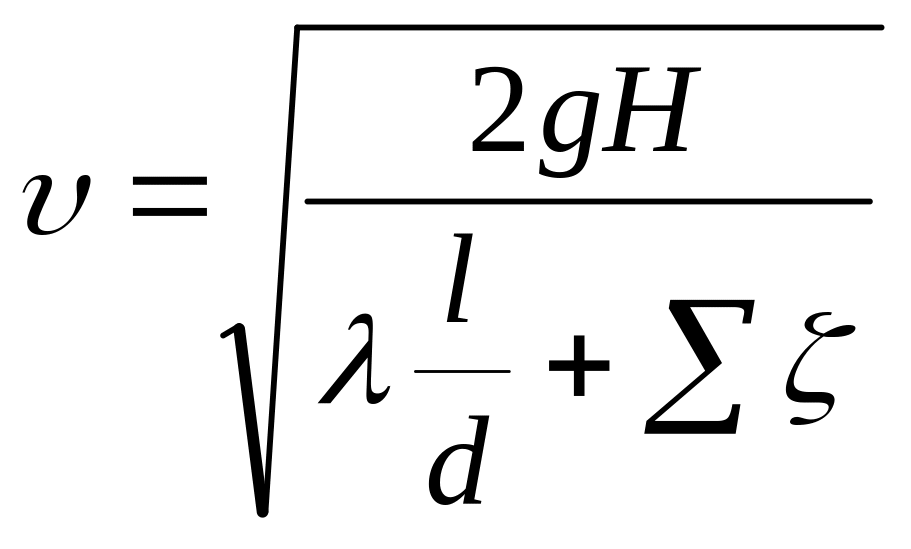. (5.6)

(коэффициент в общем случае зависит от числа Рейнольдса, а значит и от скорости).

Первое приближение. Предполагают вначале, что потери напора по длине отвечают квадратичной области сопротивления, при которой коэффициент определяется по формуле Б.Л. Шифринсона (4.9).

Подставив значение коэффициента в формулу (5.6), определяют среднюю скорость в трубе. Для проверки соответствия, принятой в первом приближении квадратичной области сопротивления, подсчитываются число . Если окажется, что , то предположение о том, что область сопротивления квадратичная, подтвердилось, и тогда первое приближение является окончательным, последующие приближения будут не нужны.

Затем находят расход жидкости .

Если окажется, что , то расчет ведется во втором приближении для доквадратичной области сопротивления по числу , полученному расчетами в первом приближении. Коэффициент определяют по формуле А.Д. Альтшуля (4.8). Далее подсчитывается и .

Если окажется, что , то необходимо продолжить расчет в третьем приближении для области сопротивления, отвечающей гидравлически гладким руслам. Расчет ведется по аналогии с предыдущими приближениями.

Задача 2. Заданы: расход жидкости , геометрические размеры трубопровода ( , , ), отметки точек ( и ), местные сопротивления ( ) и давление в конечном сечении трубопровода . Требуется найти давление в начальном сечении трубопровода .

Сначала определяют скорость жидкости, число Рейнольдса, область гидравлического сопротивления, коэффициент гидравлического трения и потери напора:

(5.7)

Из уравнения (5.5) находят давление .

Задача 3. Определить диаметр трубопровода, при котором расход жидкости равен , если заданы давления и , отметки и , местные сопротивления ( ), длина трубопровода и шероховатость его стенок .

Поскольку в левую часть уравнения (5.5) входят заданные величины, а правая часть его является функцией диаметра, то он может быть найден из этого уравнения подбором.