Пара взаимно двойственных задач лп. Основные теоремы теории двойственных задач и их применение к решению задач лп

Парой взаимно двойственных задач ЛП называются задачи (6.1) и (6.2):

(6.1)

(6.2)

где ; ; .

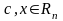Задачи (6.1) и (6.2) взаимно двойственны, т.е. если задача максимизации (6.1) – исходная, то задача минимизации (6.2) – двойственная к ней и наоборот.

Если исходная задача ЛП сформулирована в канонической форме:

(6.3)

то двойственная к ней задача имеет вид:

(6.4)

и наоборот.

Справедливы следующие основные теоремы, устанавливающие связь между оптимальными решениями взаимно двойственных задач.

Теорема 5 (первая теорема двойственности). Если одна из пары двойст­вен­­ных задач имеет оптимальный план, то и другая имеет оптимальный план и зна­­чения целевых функций задач на их оптимальных планах равны между собой, т.е. . Если же целевая функция одной из пары двойст­вен­ных задач не ограничена, то другая задача вообще не имеет допустимых планов.

Теорема 6 (вторая теорема двойственности). Для того, чтобы допустимые планы исходной (6.3) и двойственной (6.4) задач были оптима­льными, необходимо и достаточно, чтобы выполнялись условия:

(6.5)

Скалярная форма условий (6.5) имеет вид:

;

;

;

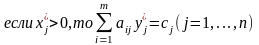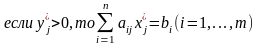т.е. если в оптимальном плане какая-либо компонента , то соответ­с­тву­ющее ей -е ограничение двойственной задачи на её оптимальном плане обращается в равенство; если оптимальный план обращает -е неравенство этой задачи в строгое неравенство, то соответствующая ему ком­по­нента в оптимальном плане двойственной задачи обращается в ноль.

Рассмотрим применение теории двойственности задач к решению задач ЛП на следующем примере.

Задача 2. Дана задача ЛП:

(6.6)

(6.7)

Требуется:

1) сформулировать двойственную задачу к задаче (6.6) – (6.7);

2) решить двойственную задачу графически;

3) найти оптимальное решение исходной задачи (6.6) – (6.7), используя теоремы двойственности.

Сформулируем задачу, двойственную к задаче (6.6) – (6.7).

Исходная задача:

,

.

Двойственная задача, по определению, будет иметь вид:

,

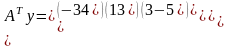Двойственная задача, записанная в скалярной, форме принимает вид:

(6.8)

Полученная задача имеет две переменные , поэтому её решение мож­но найти геометрически. Построим многоугольник допустимых решений

R, определяемый системой неравенств (6.8) (рис.3). Для этого проводим

ограничительные линии: (1) , (2) ,

(3) , (4) и штриховкой помечаем полуплоскости, определяемые неравенствами (6.8).

Рис.3

Рис. 3

Как видно из рис.3, множество R – пятиугольник OABCD. Строим линию уровня целевой функции

и перемещаем её параллельно самой себе в направлении вектора . Оптимальной вершиной R является точка С, координаты которой определим из решения системы:

.

Итак, .

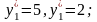
Зная оптимальный план двойственной задачи, найдём оптимальный план исход­ной задачи , используя теоремы двойственности.

По теореме 5 можно утверждать, что исходная задача (6.6)–(6.7) имеет оптимальный план , на котором целевая функция принимает значение . Сам оптимальный план получим из условия (6.5) тео­­ремы 6. Так как 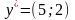имеет две положительные компоненты, то соот­ве­­тствующие им ограничения исходной задачи (6.7) на оптимальном плане обращаются в равенства:

(6.9)

При этом и , так как первое и четвёртое ограничения системы (6.8) на плане обращаются в строгие неравенства.

С учетом последнего замечания система (6.9) принимает вид:

и имеет решение , . Следовательно, оптимальный план исходной задачи ; на нём целевая функция принимает минимальное значение

.