Симплекс-таблица № 1

4 2

0 ₃ –1 3 = 9

0 ₄ 2 3 = 18

0 ₅ 2 –1 = 10

–4 –2 = 0

В этой таблице относительные оценки вычислены по формуле (4.2). Поско­льку целевая функция не содержит переменных , то вектор при это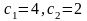м . Имеем:

,

.

Относительные оценки базисных переменных 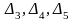равны нулю. Значение целе­­вой функции на первом опорном плане также равно нулю:

. Так как среди относительных оценок есть отрицательные то по теореме 2 план не является оптима­ль­ным. Этот план можно улучшить, поскольку среди элементов столбцов и есть положительные (теорема 4). Выбираем разрешающий столбец и разрешающую строку симплекс-таблицы №1, используя схему 1. Так как 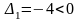, то разрешающий столбец – первый. Для выбора разре­шающей строки определим 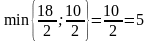, т.е. разрешающая строка – третья. Элемент , стоящий на пересечении разрешающего столбца и

разрешающей строки, назы­вается разрешающим элементом (в симплекс-таблице №1 он очерчен квадратиком). Преобразуем симплекс-таблицу №1 методом жордановых преобразований с выб­ран­­­ным разрешающим элементом

по следующим правилам (схема 2):

1) разрешающий элемент заменяется обратной величиной ;

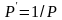2) остальные элементы разрешающей строки делятся на разрешающий элемент: ;

3) остальные элементы разрешающего столбца меняют знаки на противо­поло­ж­ные и делятся на разрешающий элемент: ;

4) оставшиеся элементы симплекс-таблицы преобразуются по правилу прямоу­го­­льника:

Э Д

Э`=(Э Р – П Д)/Р,

П Р

где 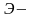преобразуемый, разрешающий элементы, образующие главную диа­го­наль, а элементы 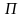и побочную диагональ символического прямоу­го­льника. Символом 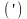отмечены преобразованные элементы симплекс-таблицы. По схеме 2 с разрешающим элементом получаем:

1)

2)

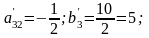
3)

4)

Результаты запишем в симплекс-таблицу № 2 и учтем, что переменная , соответ­ствующая разрешающему столбцу, стала базисной переменной, а переменная

, соответствующая разрешающей строке, стала свободной переменной.

Симплекс таблица № 2

0 2

_{5 2}

0 ₃ 1/2 5/2 = 14

0 ₄ –1 4 = 8

4 ₁ 1/2 –1/2 = 5

2 –4 = 20

Полагая в симплекс-таблице № 2 свободные переменные равными нулю, т.е. , и решая соответствующие уравнения, получим новое опорное решение , при этом значение целевой функции увеличилось: .

Так как 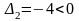и во втором столбце есть положительные эле­ме­н­ты, то согласно теореме 4 полученный план можно улучшить, переходя к но­вой симплекс-таблице № 3.

Разрешающий столбец – второй, , следовательно,

разрешающая строка – вторая, разрешающий элемент .