
- •Линейное программирование постановка задачи
- •Основные понятия линейного программирования (лп)
- •Графический метод решения простейших задач лп
- •Метод последовательного улучшения решения задачи лп (симплекс-метод)
- •Симплекс-таблица № 1
- •Симплекс-таблица № 3
- •Задача об оптимальном планировании производства
- •Симплекс-таблица № 1
- •Симплекс-таблица № 2
- •Симплекс-таблица № 3
- •Пара взаимно двойственных задач лп. Основные теоремы теории двойственных задач и их применение к решению задач лп
- •Транспортная задача
Метод последовательного улучшения решения задачи лп (симплекс-метод)
Для случая, когда число переменных более трёх, геометрический метод решения задачи ЛП становится невозможным, и тогда применяют аналитические методы. К числу таких методов относится так называемый симплекс-метод. Изложим суть симплекс-метода.
Пусть требуется решить задачу ЛП, записанную в канонической форме:

Систему
линейных уравнений
 можно записать в виде:
можно записать в виде:
 ,
(4.1)
,
(4.1)
где
 – столбцы матрицы А
системы ограничений,
– столбцы матрицы А
системы ограничений,
 – столбец свободных членов системы.
– столбец свободных членов системы.
Пусть ранг матрицы А равен m, тогда m столбцов матрицы А линейно независимы. Базисным решением системы линейных уравнений (4.1) называется решение, ненулевым компонентам которого соответствуют линейно независимые столбцы матрицы А. Если базисное решение удовлетворяет условию неотрицательности, то оно называется опорным. Опорное решение называется невырожденным, если оно содержит ровно m положительных компонент, и называется вырожденным в противном случае.
Пусть
множество
допустимых планов задачи (2.9) непусто
 и задано в виде системы (4.1). Точка
и задано в виде системы (4.1). Точка
 является вершиной многоугольника
тогда и только тогда, когда
является вершиной многоугольника
тогда и только тогда, когда
 – опорное решение (план) системы
– опорное решение (план) системы
 .
Идея симплекс-метода и состоит в
последовательном целенаправленном
продвижении по опорным планам задачи
ЛП, когда каждый последующий опорный
план не хуже предыдущего, т.е.
.
Идея симплекс-метода и состоит в
последовательном целенаправленном
продвижении по опорным планам задачи
ЛП, когда каждый последующий опорный
план не хуже предыдущего, т.е. ,
вплоть до получения оптимального плана
(или выяснения неразрешимости задачи).
При этом используются следующие теоремы.
,
вплоть до получения оптимального плана
(или выяснения неразрешимости задачи).
При этом используются следующие теоремы.
Теорема
2 (признак
оптимальности опорного плана).
Опорный план
 является оптимальным планом задачи
(2.9), если относительные оценки
является оптимальным планом задачи
(2.9), если относительные оценки
 .
(4.2)
.
(4.2)
При
этом
 называют относительной
оценкой погрешности
переменной
называют относительной
оценкой погрешности
переменной
 – вектор коэффициентов целевой функции
при базисных переменных
– вектор коэффициентов целевой функции
при базисных переменных
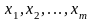 ,
т.е.
,
т.е.
 ;
;
 – столбец
матрицы ограничений А
при переменной
– столбец
матрицы ограничений А
при переменной
 ;
;
 – коэффициент
при переменной
в целевой функции.
– коэффициент
при переменной
в целевой функции.
Теорема
3 (признак
неограниченности целевой функции).
Если

для
некоторого номера
 и среди чисел
и среди чисел
 – элементов столбца
– элементов столбца
 –
нет положительных (т.е. все
–
нет положительных (т.е. все
 ),
то целевая функция задачи (2.9) не ограничена
на множестве
её допустимых планов.
),
то целевая функция задачи (2.9) не ограничена
на множестве
её допустимых планов.
Теорема
4 (о
возможности улучшения опорного плана).
Если опорный план
задачи (2.9) невырожден и некоторое
,
но среди чисел
 есть положительные (т.е. не все
),
то существует опорный план
есть положительные (т.е. не все
),
то существует опорный план такой, что
такой, что
 .
.
Переход
от одного опорного плана
к новому опорному плану
осуществляется исключением
из числа базисных переменных
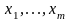 одной из этих переменных и
введением в число базисных одной из
небазисных
одной из этих переменных и
введением в число базисных одной из
небазисных
переменных
 по следующей схеме (схема 1):
по следующей схеме (схема 1):
1)
выбирают разрешающий столбец
,
соответствующий отрицательному
значению
 ;
переменная
;
переменная
 будет включена в число базисных
переменных;
будет включена в число базисных
переменных;
2) выбирают разрешающую строку, соответствующую наименьшему отношению элементов столбца свободных членов системы ограничений к соответствующим положительным элементам разрешающего столбца
 ,
,
где
минимум берётся по всем номерам
 таким, что
таким, что
 ;
переменная
;
переменная
 должна быть исключена из числа базисных
переменных.
должна быть исключена из числа базисных
переменных.
Затем систему ограничений преобразуют по схеме Жордана-Гаусса. Все вычисления записывают в таблицах, которые называют симплексными таблицами и составляют следующим образом.
Пусть
линейно независимы первые
 столбцов матрицы
столбцов матрицы
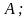
 –
базисные столбцы и система
преобразованы так, что эти столбцы
единичные, т.е.
–
базисные столбцы и система
преобразованы так, что эти столбцы
единичные, т.е.
 ,
,
 ,
… ,
,
… ,
 ,
,

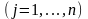 .
.
Тогда симплекс-таблица имеет вид:


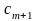
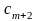


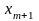






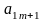

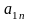 =
=


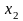


 =
=

. . . . . . . . . . . . . . . . . . .




 =
=






 =
=
Слева
в таблице указаны базисные переменные
и вектор
из коэффициентов целевой функции
при базисных переменных, вверху
– небазисные переменные
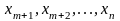 ;
соответствующие этим переменные
коэффициенты целевой функции
;
соответствующие этим переменные
коэффициенты целевой функции
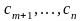 и столбцы
и столбцы
 матрицы ограничений А,
справа – столбец
матрицы ограничений А,
справа – столбец
свободных
членов и внизу – строка с обозначением
“ ”,
в которой записаны значения
относительных оценок небазисных
переменных, вычисленные по формуле
(4.2), и значение целевой функции
,
вычисленное на первом опорном плане
”,
в которой записаны значения
относительных оценок небазисных
переменных, вычисленные по формуле
(4.2), и значение целевой функции
,
вычисленное на первом опорном плане
 .
.
Проиллюстрируем решение задачи ЛП симплекс-методом на примере задачи (3.1) – (3.2), ранее решённой геометрически.
Задачу
(3.1) – (3.2) запишем в каноническом виде,
введя три дополнительные
переменные
 и заменив неравенства равенствами:
и заменив неравенства равенствами:
 (4.3)
(4.3)
Столбцы матрицы ограничений
 ,
,
 ,
,
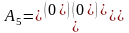
линейно независимы, т.к. определитель, составленный из элементов столбцов
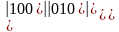 .
.
Переменные
 соответствующие
этим столбцам, – базисные переменные,
соответствующие
этим столбцам, – базисные переменные,
 небазисные (или свободные) переменные.
Положив в системе (4.3) свободные
переменные равными нулю, т.е.
небазисные (или свободные) переменные.
Положив в системе (4.3) свободные
переменные равными нулю, т.е.
 из (4.3) найдём
из (4.3) найдём
 .
Первое опорное решение будет
.
Первое опорное решение будет
 .
Для перехода к следующему опорному
решению систему (4.3) запишем в виде:
.
Для перехода к следующему опорному
решению систему (4.3) запишем в виде:

и составим симплекс-таблицу № 1.
