Линейное программирование постановка задачи

Разнообразные проблемы экономики, организации транспортных перевозок и других видов хозяйственного планирования часто ставятся в форме задач оптимизации, т.е. задач поиска экстремума (минимума или максимума) некоторой функции (называемой целевой) при наличии каких-либо дополнительных ограничений. Если целевая функция является линейной по переменным 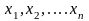, а ограничения задаются в виде системы равенств или неравенств, линейных относительно этих переменных, то соответствующая задача оптимизации (программирования) называется линейной.

К задачам линейного программирования (ЛП) приводят, в частности, проблемы эффективного использования ограниченных ресурсов сырья или мощностей оборудования. Рассмотрим для примера построение математической модели следующей экономической задачи.

Задача. Нефтеперерабатывающий завод производит за месяц 1500 т алкилата, 1200 т крекинг бензина и 1300 т изопентона. В результате смешивания этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1 т бензина сортов А и Б соответственно равна 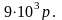и Определить месячный план производства бензина сорта А и Б, максимизирующий стоимость выпущенной продукции.

Сформулируем эту задачу математически. Пусть и – месячный объем производства (в тоннах) бензина сортов А и Б соответственно. Тогда стоимость (в тыс. р.) месячного производства бензина обоих сортов определяется целевой функцией

. (А)

Если в какую-либо смесь объема 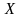составляющие компоненты входят в пропорции , то объемы этих компонентов равны

.

С учетом этого замечания, а также принимая во внимание, что для получения тонны бензина сорта А и тонны бензина сорта Б расходуется не более чем 1500, 1200 и 1300 тонн соответствующих компонентов, заключаем, что должны выполняться следующие ограничения:

(Б)

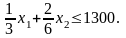
Кроме того, по физическому смыслу

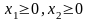. (В)

Следовательно, задача состоит в том, чтобы найти значения и , удовлетворяющие ограничениям (Б)–(В) и максимизирующие функцию . Это типичная задача линейного программирования. Найденная линейная целевая функция (А) совместно с системой ограничений (Б)–(В) образуют математическую модель рассмотренной задачи.

Основные понятия линейного программирования (лп)

Общая задача ЛП формулируется следующим образом: найти оптимум (максимум или минимум) линейной целевой функции

(2.1)

переменных при следующих линейных ограничениях:

, (2.2)

, (2.3)

, (2.4)

. (2.5)

Здесь – заданные постоянные.

Стандартная задача ЛП состоит в определении максимума функции (2.1) при ограничениях-неравенствах (2.2) и условиях (2.5), т.е. имеет вид

(2.6)

Каноническая (или основная) задача ЛП состоит в определении максимума функции (2.1) при ограничениях-равенствах (2.3) и условиях (2.5):

(2.7)

Задачу ЛП можно записать более компактно, если ввести обозначения:

– матрица ограничений размерности , – вектор-

сто­л­бец свободных членов, – вектор-строка коэффициентов целевой функции, – n-мерный вектор пространства , который в одних случаях рассматриваем как вектор-строку, а в других (опуская знак транспонирования) – как вектор-столбец.

Тогда стандартная задача (2.6) и каноническая задача (2.7) принимают соответственно вид:

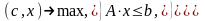(2.8)

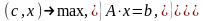(2.9)

Здесь – скалярное произведение векторов и , т.е.

,

– произведение матрицы на вектор-столбец .

Вектор , удовлетворяющий ограничениям (2.2) –(2.5), называется допустимым решением (или планом). Множество всех допустимых планов задачи ЛП обозначим через .

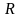Допустимый план , доставляющий экстремум целевой функции, называется оптимальным планом (решением) задачи ЛП. Множество всех оптимальных планов обозначим через .

Если множества и не пустые , то задача ЛП разрешима, в противном случае говорят о неразрешимости этой задачи.

Различают два типа неразрешимости: НР1 – целевая функция не ограничена на непустом множестве ; НР2 – множество допустимых планов пусто ( ).

Любую задачу ЛП можно свести как к стандартной, так и к канонической формам, используя следующие правила:

1) Чтобы перейти от минимизации к максимизации целевой функции , следует умножить целевую функцию на (–1) и использовать равенство

,

т.е. задача

соответствует задаче

.

2) Чтобы изменить ограничение-неравенство на неравенство проти­во­по­лож­ного смысла следует умножить обе части неравенства на (–1):

.

3) Чтобы перейти от ограничения-неравенства к равенству, нужно ввести дополнительную (слабую) переменную :

4) Чтобы перейти от ограничения-равенства к неравенству, следует заменить равенство на два противоположных неравенства:

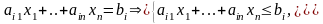
Пример. Привести к каноническому виду задачу ЛП:

,

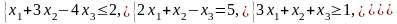
Перейдём к задаче на максимум:

.

Введём дополнительные переменные и ( , ), заменив ограничения-неравенства на равенства:

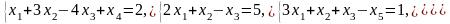
В результате получили следующую задачу ЛП, записанную в канонической форме:

,