1.4. Назначение поясных швов (определение катета шва)

Так как балка работает с учетом пластических деформаций, то швы выполняем двухсторонние, автоматической сваркой в лодочку, сварочной проволокой Св. – 0.8А.

По формуле определяем толщину шва в сечении x = 100 см, под первой от опоры вертикальной силы, где сдвигающая сила максимальна.

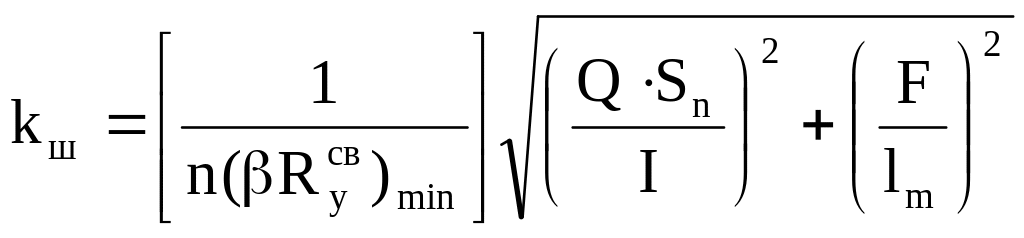
k = [1/2 ∙ 18.97] ∙ [(728.5 ∙ 1292 / 130 522)² + (562.7 / 18.0)²] ^½

k = 0.5 см,

где по таблице 5.1 /2/ определяем R = 180 МПа или R = 18 кН/см , а по приложению 4 R = 165 МПа = 16.5 кН/см

По таблице 5.3 /2/ определяем = 1.1; = 1.15

Далее определяем более опасное сечение шва:

∙ R = 1.1∙ 18 = 19.8 кН/см > ∙R = 1.15 ∙ 16.5 = 18.97 кН/см

S = b ∙ t ∙ = 20 ∙ 2 ∙ 64.6 / 2 = 1292 см

F – расчетная сосредоточенная нагрузка, F = 562.7 кН – опорные реакции колес крана.

l = b + 2∙t = 15 + 2∙1.6 = 18 см – длина передачи нагрузки на стенку балки.

b – длина передачи местной нагрузки на балку.

По таблице 5.4 /2/ принимаем. Минимально допустимый при толщине пояса t = 16 мм шов, k = 5 мм, что не меньше получившегося по расчету k = 5.0 мм.

1.5. Размещение ребер жесткости. Проверка местной устойчивости полок балок, стенки балки

1) Проверка устойчивости сжатого пояса производится в месте максимальных напряжений в нем – в середине пролета балки, где возможны пластические деформации.

Проверку ведем по формуле

Рассчитываем:

h / t = 64.6 / 1.0 = 64.6 > 2.7 ∙ = 63.0

b / t = (20 – 1) / 3.2 = 5.94 < 0.11∙ h / t = 7.11 < 0.5

7.11 < 12.79

Проверка показала, что местная устойчивость пояса обеспечена.

2) Проверяем устойчивость стенки. Первоначально определяем необходимость постановки ребер жесткости по формуле.

λ_ст = h / t = (64.6 / 1) ∙ (31.5 / 2.06 ∙ 10 ) = 2.53 > 2.2

т.е. вертикальные ребра жесткости необходимы. Определяем предварительную длину «а» зоны использования пластических деформаций в стенке по формуле:

a = l = 662 ∙ [1 – (1/1.1) ∙ (646/630)] = 172.4 см

По формуле устанавливаем необходимость проверки устойчивости стенки. Расчет = 2.53 > 2.2 показал, что проверку устойчивости стенки следует производить. Находим значения М и Q в сечении 2-2 на расстоянии x = 1,50 м = 150 см от опоры, при наиболее неблагоприятном расположении колес крана.

М^х2 = 1.05 · [562.7 · (0.80 + 1.173)] ∙ 0.85 = 990.9 кН·м

Q = 1.05 · [562.7 · (0.733 + 0.500)] ∙ 0.85 = -619.2 кН.

Определяем действующие напряжения:

= = 99090 ∙ 63 / 3943 ∙ 66.2 = 23.9 кН / см

= = 619.2 / 63 ∙ 1.0 = 9.8 кН / см

Определяем критические напряжения.

По формуле находим:

= 10.3 ∙ (1 + 0.76 / ) ∙ R / , где h = h ; = = 2.53

= a / h = 150 / 63 = 2.38;

R = 15.0 кН / см

= 10.3 ∙ (1 + 0.76 / 2.38 ) ∙ 15.0 / 2.53 = 27.38 кН / см

По формуле определяем:

= ( ) = 0.8 ∙ (20 / 63) ∙ (1.6 / 1) = 1

По таблице 23 /1/, при = 1 и a / h = 2.38, → c = 45.6, поэтому σ определяем по формуле:

= 45.6 ∙ 31.5 / 2.53 = 224.4 кН / см

Подставляем все значения в формулу:

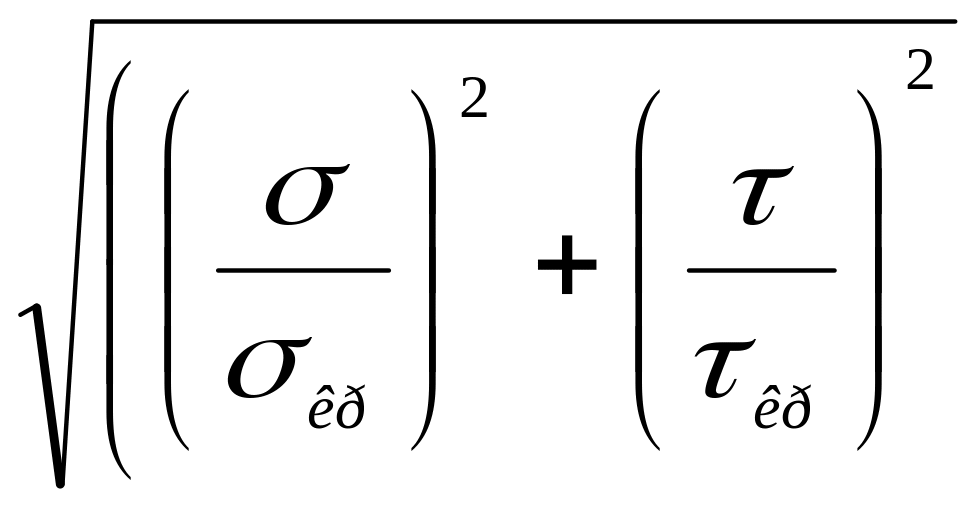= [(23.9 / 224.4) + (9.8 / 27.38) ] =

= [0.011 + 0.13] = 0.38 < = 1

Проверка показала, что устойчивость стенки обеспечена и постановка ребер жесткости на расстоянии a = 150 см > 2h = 2 ∙ 63 = 126 см возможна. Устанавливаем ребра жесткости конструктивно на расстоянии а = 150 см