Практические занятия № 6. 7. 8 Тема: Приближённые методы решения обыкновенных дифференциальных уравнений. Метод Пикара – приближённый аналитический метод.

Задача Коши: решить ОДУ y` = f(x,y) c начальным условием y(x₀)=y_0/

Задача Коши имеет единственное решение, если функция f(x,y) непрерывна в окрестности точки (x₀,y₀) и имеет ограниченную частную производную по y – f`_y.

Формула Пикара: .

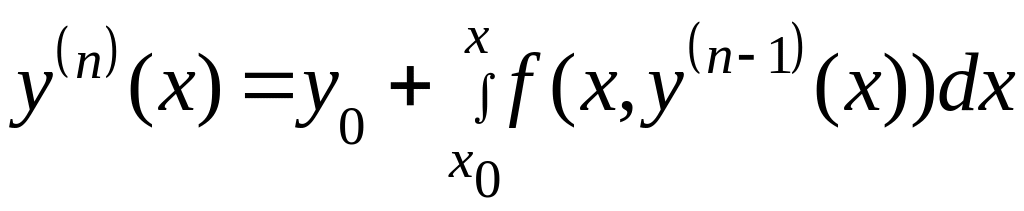В области R{|x-x₀|<a;|y-y₀|<b} погрешность оценивается формулой:

где M=max|f(x,y)|; N=max|f`_y(x,y)|; h=min(a,b/M).

Пример. Методом Пикара найти три первых приближённых решения дифференциального уравнения и оценить погрешность:

y`=x-y; y(x=0)=1; на отрезке [0;0,5]. ;

;

;

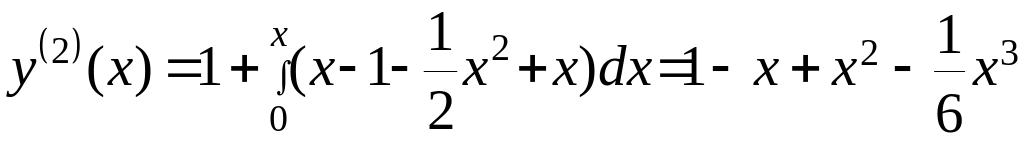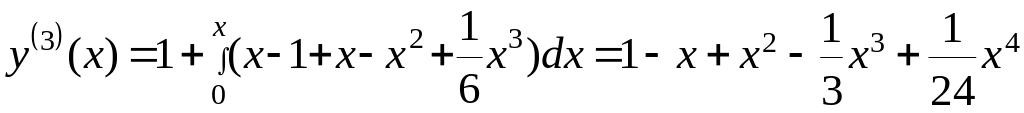X	X2	X3	X4	Y(1)	Y(2)	Y(3)
0	0	0	0	1,	1,	1,
0,1	0,01	0,001	0,0001	0,9050	0,9098	0,9098
0,2	0,04	0,008	0,0016	0,8200	0,8397	0,8377
0,3	0,09	0,027	0,0081	0,7450	0,7855	0,7650
0,4	0,16	0,064	0,0256	0,6800	0,7494	0,7397
0,5	0,25	0,125	0,0625	0,6250	0,7292	0,7109

Для оценки погрешности каждого из приближённых решений вычислим.

n=1: x=[0;0,5]; y=[1;0,625]; f(x,y)=x-y; max|f(x,y)| =1=M;

f`<sub>y</sub>(x,y)=x-1; max|f`(x,y)|=1=N;

h=min(|x-x₀|=0,5;|y-y₀|=0,375)=0,375;

- погрешность первого приближения.

n=2: x=[0;0,5]; y=[1;0,7292]; M=1; N=1; h=min(0,5;0,2708)=0,2708;

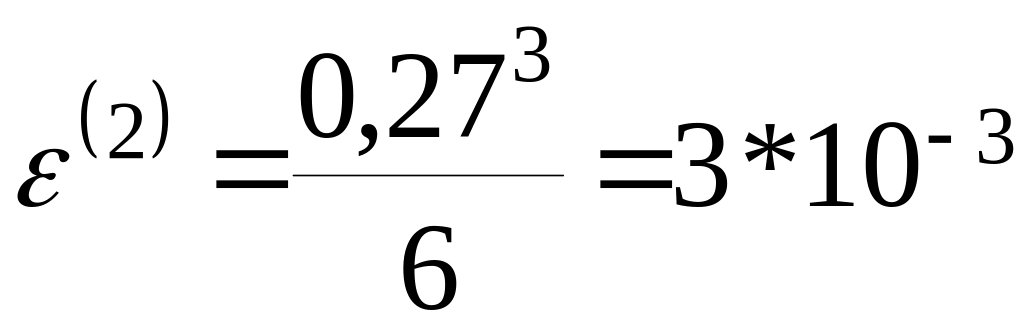-погрешность второго приближения.

n=3: x=[0;0,5]; y=[1;0,7109]; M=1; N=1; h=min(0,5;0,29)=0,29;

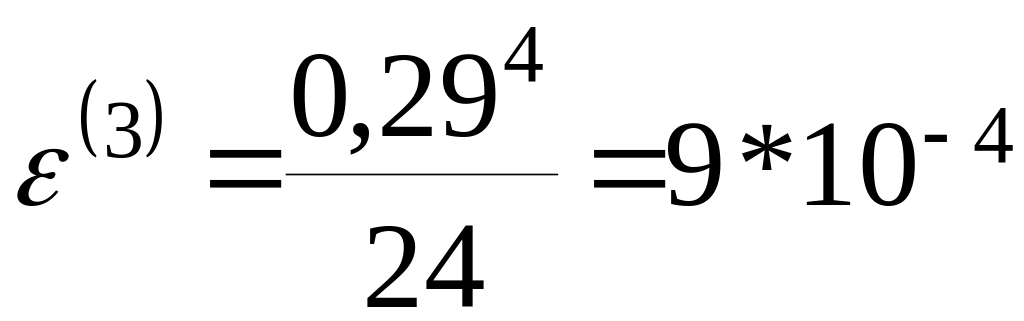-погрешность третьего приближения.

Метод Эйлера – численный метод первого порядка точности.

Расчётная формула: где .

Оценку погрешности выполняют методом Рунге путём двойного просчёта: с шагом h – y_n, и с шагом h/2 – y^*_n.. Пусть y(x_n) – точное решение в точке x_n, тогда погрешность в этой точке:

|y^*_n – y(x_n)| < |y^*_n – y_n| .

Пример. Решить дифференциальное уравнение 1-го порядка : y`=y – 2x/y c начальным условием y(x=0)=1 на интервале [0;1] c шагом h=0,2.

k	xk	yk	F(xk,yk)	yk	yточное
0	0	1,0000	1,0000	0,2000	1,0000	0
1	0,2	1,2000	0,8667	0,1733	1,1832	0,0168
2	0,4	1,3733	0,7805	0,1581	1,3416	0,0317
3	0,6	1,5315	0,7458	0,1495	1,4832	0,0483
4	0,8	1,6811	0,7254	0,1458	1,6124	0,0687
5	1,0	1,8268			1,7320	0,0948

Метод Эйлера даёт грубое приближение к точному решению и по мере удаления от начальной точки погрешность растёт.