Типы балок

Типы опор балок Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов. 1. Подвижная' шарнирная опора (рис. а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка. Схематическое изображение подвижной шарнирной опоры дано на рис. б. Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений. 2. Неподвижная шарнирная опора (рис. в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие — горизонтальную и вертикальную. 3. Жесткая заделка, или защемление (рис. г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент). Балка с одним заделанным концом называется консольной балкой или просто консолью. Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения — уравнения перемещений. диф. соотношение

Выделим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dz. Так как вся балка находится в равновесии, то и элемент dz будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Qy  и  Mx во бщем случае меняются вдоль оси балки, то в сечениях элемента dz будут возникать поперечные силы Qy и Qy+ dQy, а также изгибающие моменты Mx  иMx+dMx.

Из условия равновесия выделенного элемента получим:

, следовательно

;     (6.5)

, следовательно

(6.6)

Первое из двух записанных уравнений дает условие

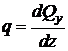                        (6.7)

Из второго уравнения, пренебрегая слагаемым   как бесконечно малой величиной второго порядка, найдем

                                       (6.8)

Рассматривая полученные выражения, совместно можем получить

                                        (6.9)

Полученные соотношения называют дифференциальными зависимостями Д.И. Журавского при изгибе.

Анализ дифференциальных зависимостей при изгибе по­зволяет установить некоторые особенности (правила) построения эпюр изги­бающих моментов и поперечных сил:

- на участках, где нет распределенной нагрузки q, эпюры Q ограничены прямыми, параллельными базе, а эпюры М - наклонными прямыми;

- на участках, где к балке приложена распределенная нагрузка q, эпюры Q ограничены наклонными прямыми, а эпюры М - квадратичными параболами. При этом, если эпюру М строим «на сжатом волокне», то выпуклость параболы будет направлена против направления действия q, а экстремум будет расположен в сечении, где эпюра Q пересекает базовую линию;

         - в сечениях, где к балке прикладывается сосредоточенная сила, на эпюре Q будут скачки на величину и в направлении данной силы, а на эпюре М - пе­регибы, острием направленные в направлении действия этой силы;

 - в сечениях, где к балке прикладывается сосредоточенный момент, на эпю­ре Q изменений не будет, а на эпюре М - скачок на величину этого момента;

 - на участках, где Q>0, момент М возрастает, а на участках, где Q<0, мо­мент М убывает.