Методические указания

Программа курса «Основы высшей математики» агрономических специальностей содержит семь тем. После изучения теоретического курса студент выполняет одну контрольную работу.

Для изучения курса рекомендуется следующая литература:

1. Зайцев А.И. «Высшая математика», М., 1991

2. Кудрявцев В.А.,Демидович Б.П. «Краткий курс высшей математики» М., 1975

3. Маркович Э.С. «Курс высшей математики с элементами теории вероятностей и математической статистики» М., 1972

4. Гмурман В.Е. «Теория вероятностей и математическая статистика» М., 1972

Студент выполняет тот вариант, который совпадает с его номером по списку.

Тема :Основы сведения из математической статистики. Статистические оценки параметров распределения. Понятие о корреляционной таблице.

Литература: [1]-Гл.XIII, &13.1–13.3, 13.5-13.7;

Гл.XIV, &14.1–14.2,14.4;

[3]-Ч.II,Гл.V, &15,17-19;

Гл.VI, &21-23,25;

[4]-Гл.XV, &1-6,8; Гл.XVI, &1-5,

&8-10,13,14,23; Гл.XVIII, &1-5,7-9.

Примеры решения задач.

Задача 1. Результаты обследования 20 семей по числу членов оказалось таким: 2;5;3;4;1;3;6;2;4;3;4;1;3;5;2;3;4;3;4;3. Получить по этим данным вариационный ряд и построить полигон распределения относительных частот.

Решение:

Проводим ранжирование данного ряда:

1; 1; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 6.

Определяем частоты различных вариантов. Варианты 1 встречается в ряду 2 раза, следовательно, m₁=2. Аналогично, m₂=3, m₃=7, m₄=5, m₅=2, m₆=1.

Определяем относительные частоты наблюдавшихся в выборке вариантов по формуле: , где n=20 – объем выборки.

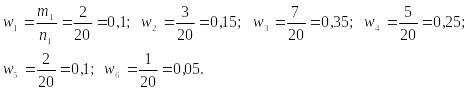
Сумма всех относительных частот равна 1, значит, вычисления сделаны верно.

Результаты вычисления сводим в таблицу:

Варианты xi	1	2	3	4	5	6
частота mi	2	3	7	5	2	1
Относительная Частота wi	0,1	0,15	0,35	0,25	0,1	0,05

Используя таблицу, строим полигон распределения относительных частот:

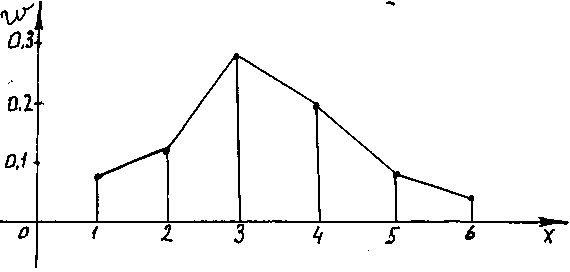
Задача 2. По данным показателям, полученным в тестах, составить интервальный ряд распределения и начертить гистограмму: 13,9; 12,4; 13,1; 6,3; 11,8; 11,6; 10,5; 10,4; 10,6; 11,3; 15,1; 11,7; 11,3; 10,2; 11,0; 10,7; 8,2; 9,6; 10,2; 15,1.

Решение:

Записываем исходные данные в виде ранжированного ряда: 6,3; 8,2; 9,6; 10,2; 10,2; 10,4; 10,5; 10,6; 10,7; 11,0; 11,3; 11,3; 11,6; 11,7; 11,8; 12,4; 13,1; 13,9; 15,1; 15,1. Диапазон изменения вариантов в выборке 6-16. Разбиваем его на пять интервалов с размером каждого интервала . Размер интервала выбирается произвольно, но следует иметь в виду, что чем меньше интервал и чем больше их количество, тем точнее результаты. Определим частоту попадания вариантов выборки в каждый интервал и соответствующие относительные частоты. Результаты расчетов сводим в таблицу:

Интервалы значений Урожайности	6-8	8-10	10-12	12-14	14-16
Частота варианта mi	1	2	12	3	2
Относительные частоты wi	0,05	0,1	0,6	0,15	0,1
Плотность относительных Частот рi	0,025	0,05	0,3	0,075	0,05

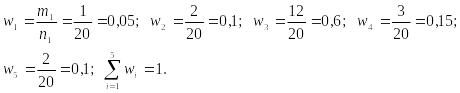
Находим плотность относительных частот р_i вариантов по формуле (четвертая строка в таблице):

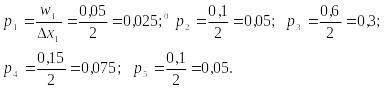
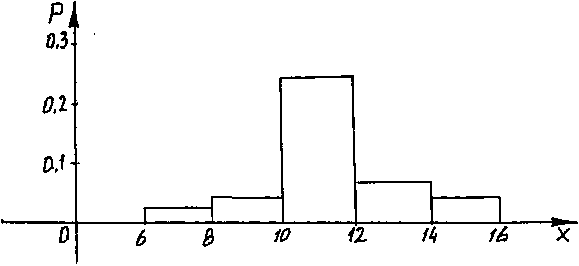
Строим гистограмму, которая показывает зависимость плотности относительных частот от значений вариантов:

Задача 3. Даны результаты обследования 25 единиц выборки:

6; 11; 9; 6; 6; 7; 6; 8; 9; 9; 11; 10; 6; 7; 6; 8; 9; 10; 4; 9; 10; 7; 8; 9; 6. Определить: 1)величину, которую следует принять за среднею генеральную совокупность; 2)величину, которую следует принять за дисперсию генеральной совокупности; 3) доверительный интервал с границами .