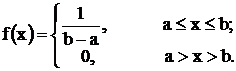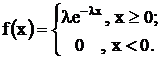1.Формула полной вероятности. Формула Байеса.

Формулы полной вероятности и Байеса.

Пусть в условиях эксперимента событие   появляется совместно с одним из группы несовместных событий (гипотез)  , образующих полную группу  , известны или можно установить априорные вероятности   каждой из гипотез и условные вероятности  события   при условии, что осуществилась та или иная гипотеза, тогда вероятность события   определяется по формуле полной вероятности:

где  – вероятность гипотезы  ;  – условная вероятность события   при выполнении гипотезы  .

ФОРМУЛА БАЙЕСА Пусть события    образуют полную группу несовместных событий ( ) и пусть событие   происходит обязательно с одним из них  . Предположим событие   произошло, тогда вероятность того, что оно произошла именно с   определяется формулой:

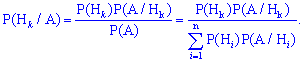
2. Формула Бернулли. Формула Пуассона.

Независимые испытания. Формула Бернулли

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. p=P(A), а вероятность противоположного события (событие А не наступило) - буквой 

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

Формула Пуассона.

Если вероятность   появления события   в отдельном испытании достаточно близка к нулю  , то даже при больших   значениях количества испытаний вероятность, вычисляемая по локальной теореме Лапласа, оказывается недостаточно точной. В таких случаях используют формулу, выведенную Пуассоном.

ТЕОРЕМА ПУАССОНАЕсли вероятность   наступления события  в каждом испытании постоянна, но достаточно мала, число независимых испытаний   достаточно велико, при этом сочетания   меньше десяти то вероятность того, что в количестве   испытаниях событие   наступит ровно   раз примерно равна

где  Для формулы Пуассона используют таблицы табулирования функции  .

3. Локальная и интегральная теоремы Лапласа. Функция Лапласа.

Если количество независимых испытаний достаточно большое применения формулы Бернулли становится трудоемким. Для упрощения вычислений применяют локальную и интегральную теоремы Лапласа, которые дают близкий к формуле Бернулли результат при большом количестве испытаний и не требуют больших вычислений.

ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА

Вероятность того, что в   независимых испытаниях с вероятностью появления события   равной   событие   наступит ровно   раз (безразлично в какой последовательности) определяется по приближенной формуле

-локальная формула Лапласа.

где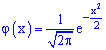 – Функция Гаусса,

– аргумент функции Гаусса;

– вероятность противоположного события  .

ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА

Вероятность, что в   независимых испытаниях событие   с вероятностью появления   наступит не менее   раз и не более   (независимо от последовательности появления) приближенно определяется зависимостью

где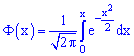 – интегральная функция Лапласа;

– аргументы интегральной функции распределения;

 – вероятность невыполнения события  .

4. Функция распределения, полигон и гистограмма частот дискретной случайной величины.

Функция распределения дискретной случайной величины

Если  - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид

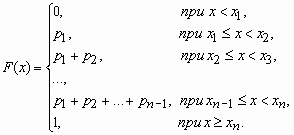
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

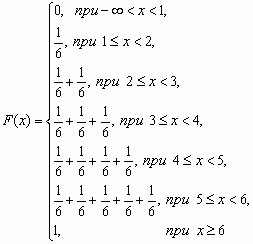
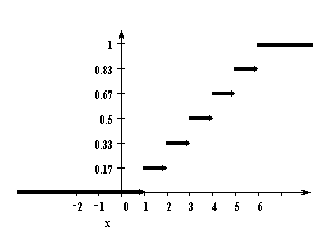
Графическое изображение статистических данных

Статистическое распределение изображается графически с помощью полигона и гистограммы.

Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами ; полигоном частостей – с координатами , где , . Полигон служит для изображения дискретного статистического ряда. Полигон частостей является аналогом многоугольника распределения дискретной случайной величины в теории вероятностей.

Определение. Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси и длины их равны длинам частичных интервалов , а высоты равны отношению: - для гистограммы частот; - для гистограммы частостей.

Гистограмма является графическим изображением интервального ряда. Площадь гистограммы частот равна , а гистограммы частостей равна 1.

Можно построить полигон для интервального ряда, если его преобразовать в дискретный ряд. В этом случае интервалы заменяют их серединными значениями и ставят в соответствие интервальные частоты (частости). Полигон получим, соединив отрезками середины верхних оснований прямоугольников

5. Дифференциальная и интегральная функции распределения непрерывной случайной величины

Дифференциальная функция распределения

Дифференциальная функция распределения непрерывных случайных величин f(x) и ее свойства.

Способ, когда закон распределения непрерывной случайной величины задают с помощью интегральной функции, не является единственным. Гораздо чаще его задают с помощью дифференциальной функции распределения вероятностей, которую обозначают f(x). Эту функцию также называют плотностью распределения вероятностей.

Дифференциальной функцией распределения называется 1-я производная от интегральной функции распределения .

Для дискретной случайной величины функция распределения будет иметь разрывы, и поэтому она не применяется для дискретных величин.

Интегральная функция распределения

Интегральной функцией распределения называется функция F(x), которая определяет вероятность того, что при испытаниях случайная величина Х примет значение меньше, чем  х .

 

Свойства интегральной функции распределения

1. Значения  интегральной  функции удовлетворяют двойному неравенству: 0<= F(x)<= 1 2.  F(x) – неубывающая функция. Следствие 1. Вероятность того, что непрерывная случайная величина примет значение между а  и  b равна приращению интегральной функции на этом интервале P(a < x < b)= F(a) – F(b)

 

Следствие 2. Вероятность того, что непрерывная функция примет одно заранее определеное значение равна 0. Это следует из того,  что  F(a) – F(а) = 0 3.  Если все возможные значения случайной величины принадлежат интервалу (a , b) , то

6.Равномерный закон распределения.

 Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:

Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда с=1/(b-a). Функцию f(x) можно представить в виде

  

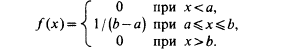
График функций f(x):

Нормальный закон  распределения.

Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

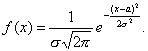
где а и s—некоторые постоянные, называемые параметрами нормального распределения.

Функция распределения F(x) в рассматриваемом случае принимает вид

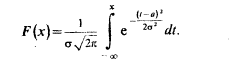
Параметр а- есть математическое ожидание НСВХ, имеющей нормальное распределение, s - среднее квадратическое отклонение, тогда дисперсия равна

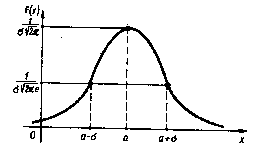
 Выясним геометрический смысл параметров распределения а и s. Для этого исследуем поведение функции f(x). График функции f(x) называется нормальной кривой.

Свойства функции f(x):

1°. Областью определения функции f(x) является вся числовая ось.

2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.

3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.

      4°. Функция f{x) имеет в точке х = a  максимум, равный

5°. График функции f(x) симметричен относительно прямой х = а.

6°. Нормальная кривая в точках х = а +s  имеет перегиб,

  

 

На основании доказанных свойств построим график плотности нормального распределения f(x).

 

 

 

 

 

Как видно из рисунка, нормальная кривая имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса.

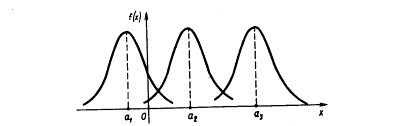
При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо .

 

 

 

 

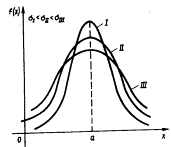
При изменении параметра  s изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение  функции f(x) убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра  кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением s  кривая стягивается к прямой х=а .

 

 

 

 

 

 

Использование формул  f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим  формулам  можно упростить, если от нормального распределения с произвольными параметрами а и s перейти  к нормальному распределению с параметрами а=0, s = 1.

 Функция плотности нормального распределения f(x) с параметрами а=0, s  =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

Функция плотности и интегральная функция стандартной нормальной СВ будут иметь вид:

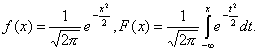
 Показательное распределение.

 Определение: Непрерывная случайная величина X, функция плотности которой задается выражением

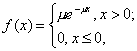
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение.

Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.

Показательное распределение определяется только одним параметром m.

Найдем функцию распределения показательного закона, используя свойства дифференциальной функции распределения:

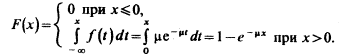
Графики дифференциальной и интегральной функций показательного распределения имеют вид: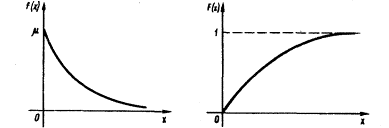 

7. Числовые характеристики M(x), D(x) основных законов распределения для непрерывных СВ (равномерный, показательный, нормальный).

Равномерный закон распределения случайной величины

Пусть случайная величина Х может принимать любые значения в пределах отрезка  . Закон распределения называется равномерным, если

Найдём математическое ожидание  .

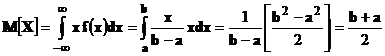Математическое ожидание случайной величины, равномерно распределенной на отрезке   , равняется середине этого отрезка.

         Дисперсия:    

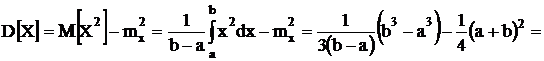
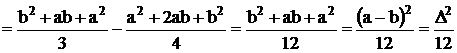
Величина    называется поправкой  Шеппарда.

Показательный закон распределения

Показательный закон распределения случайной величины широко применяется в теории надежности.

Случайная величина распределена по показательному закону, если

 

Теорема: Математическое ожидание и среднеквадратическое отклонение случайной величины, распределенной по показательному закону с параметром  , равны: .

 НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Нормальный закон распределения характеризуется плотностью вероятности вида:

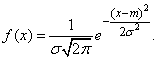
И соответственно бла бла бла

.

.

,

10. Равномерное и показательное распределения, функция надежности.

Равномерный закон распределения случайной величины

Пусть случайная величина Х может принимать любые значения в пределах отрезка  . Закон распределения называется равномерным, если

Найдём математическое ожидание  .

Математическое ожидание случайной величины, равномерно распределенной на отрезке   , равняется середине этого отрезка.

         Дисперсия:    

Показательный закон распределения

Показательный закон распределения случайной величины широко применяется в теории надежности.

Случайная величина распределена по показательному закону, если

 

Найдем интегральную функцию 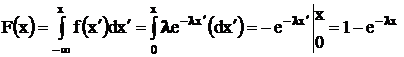. 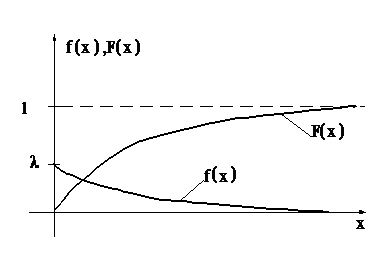Ecли в качестве переменной  используется   время ,   то    - показательный закон надежности и λ –интенсивность отказов.  На практике отмечено, что при заданной интенсивности отказов λ вероятность безотказной работы элемента электронной техники на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности интервала t .

Теорема: Математическое ожидание и среднеквадратическое отклонение случайной величины, распределенной по показательному закону с параметром  , равны: .

Функция надежности.

Пусть некоторое устройство начинает работать в момент времени t₀ = 0, а по истечении времени длительностью t происходит отказ. Обозначим через Т НСВ - длительность времени безотказной работы устройства. Если устройство проработало безотказно время меньшее t, то, следовательно, за время длительностью t наступит отказ. Тогда функция распределения F(t)=P(T<t)=1- e^-mt определяет вероятность отказа устройства за время t.

вероятность противоположного события- безотказной работы за время t:

 .

Функция R(t) называется функцией надежности.