Гидравлика — наука, изучающая законы равновесия и движения различных жидкостей и методы применения этих законов для решения практических задач. Законы гидравлики используются при проектировании гидросистем автомобиля и двигателя, изучении явлений в процессе наполнения в цилиндрах двигателя и при истечении топлива в карбюраторе. Гидравлика состоит из двух основных частей: гидростатики, изучающей законы равновесия жидкостей, и гидродинамики, изучающей законы движения жидкостей. Основные свойства капельных жидкостей. В понятие «жидкость» включают все тела, для которых свойственна текучесть, т.е способность сильно изменять свою форму под действием сколь угодно малых сил. В это понятие включают как жидкости обычные, называемые капельными, так и газы. Важной особенностью капельных жидкостей является то, что они ничтожно мало изменяют свой объем при изменении давления. Газы же обладают большой сжимаемостью. Несмотря на это различие, законы движения капельных жидкостей и газов при определенных условиях можно считать одинаковыми. Основным из этих условий является малая скорость течения газа по сравнению со скоростью распространения в нем звука. В дальнейшем под термином «жидкость» - будем понимать капельную жидкость.

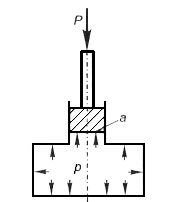
В 1663 г. французский физик Б. Паскаль опубликовал закон о передаче внешнего давления в жидкости, который до сих пор именуется законом Паскаля. По этому закону всякое изменение давления в какой-либо точке покоящейся капельной жидкости, не нарушающее ее равновесия, передается в другие точки без изменения. Следовательно, если к поршню с площадью днища а в  заполненном жидкостью закрытом сосуде приложить силу Р,  то она уравновесится силой давления жидкости р = P/а на этот поршень и по закону Паскаля будет действовать в любой точке и на поверхности сосуда. Жидкости характеризуются следующими физическими свойствами: плотностью, удельным весом, удельным объемом, сжимаемостью, вязкостью.

Плотностью ? (кг/м3) называют массу жидкости, заключенной в единице объема:

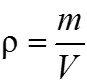
Для дистиллированной воды при 4 °С ? = 1000 кг/м3. Удельным весом ? (Н/м3) называют вес единицы объема жидкости:

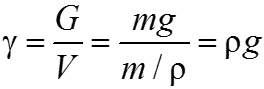
Для дистиллированной воды при 4 °С ? = 9806 Н/м3. Удельным объемом  v (м3/кг) жидкости называют объем, зани­маемый единицей массы жидкости:

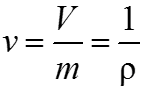
Сжимаемость (объемная упругость) жидкости характеризует­ся коэффициентом сжимаемости ?v. Отношение относительного изменения объема жидкости ?v/v— к  изменению давления ?pи называется коэффициентом сжимаемости (объемного сжатия)

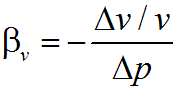
Знак «минус» в формуле обусловлен тем, что положительно­му приращению давления р соответствует отрицательное прира­щение, т.е. уменьшение объема v. При изменении давления до 500 атм (49 МПа) коэффициент ?v  для воды практически постоянен и равен 4,9 • 10-10 м2/Н. Вязкость — это свойство жидкости оказывать сопротивление относительному  движению (сдвигу) слоев жидкости. Динамическая вязкость ? показывает, какую работу на единицу объемного расхода надо совершить для преодоления сил внутреннего трения. Единицей динамической вязкости является Па • с:

В практических расчетах часто пользуются кинематической вязкостьюv (м2/с):

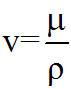
Вязкость  капельных жидкостей уменьшается при увеличении температуры. Дня упрощения теоретических исследований и выводов Л. Эйлер ввел понятие «идеальная жидкость» — воображаемая  жидкость, которая абсолютно подвижна, несжимаема и не обладает вязкостью, т.е. при движении в ней не возникают силы внутреннего трения. В гидродинамике изучаются явления в движущейся жидкости. Под потоком жидкости понимают движущуюся массу жидкости, полностью или частично ограниченную поверхностями. Поверхности раздела могут быть твердыми или образованными самой жидкостью на границе раздела фаз. Из-за сложности учета влияния всех факторов при движении потока действительное движение жидкости заменяют упрощенной моделью. В основе изучения гидродинамики лежит так называемая струйчатая модель движения. Эта схема предполагает, что поток жидкости со­стоит из бесконечно большого числа элементарных струек. Живым сечением потока называется площадь сечения потока, проведенного перпендикулярно к направлению линий тока и ограниченного его внешним контуром. Площадь живого сечения потока равна сумме площадей живых сечений элементарных струек. Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени. Различают:

объемный (Q) :   

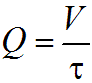
массовый (Qm) :

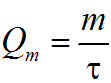
весовой (G)         

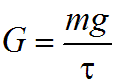
расходы жидкости. Где V— объем жидкости; m — масса жидкости; ? — время.

Объемный расход потока с живым сечением F определим с использованием понятия средней скорости потока wcp:

Средняя скорость — это условная скорость потока, которая считается одинаковой для всех частиц данного сечения, но по­добрана так, что расход, определенный по ее значению, равен истинному значению расхода. Если несжимаемая жидкость движется без разрывов, то при установившемся движении объемный расход для всех живых се­чений потока постоянен, т.е. можно записать, что вдоль потока

Это уравнение называют уравнением неразрывности потока, оно является первым основным уравнением гидродинамики. Из него следует, что средние скорости обратно пропорциональны площадям соответствующих живых сечений потока. Уравнение Бернулли является вторым основным уравнением гидродинамики, которое устанавливает связь между скоростью и давлением в потоке жидкости. Для потока реальной вязкой жидкости уравнение Бернулли, написанное для двух произвольно взятых сечений 1 и 2 по ходу потока, имеет следующий вид:

где р - гидромеханическое давление (или просто давление); ? — безразмерный коэффициент Кориолиса, учитывающий неравно­мерность распределения скоростей по сечению потока жидко­сти. При течении в круглой трубе ? = 1,05... 1,1 для турбулентного движения и ? = 2 — для ламинарного;  ?w2-динамическое давление; pgz — весовое давление; z — высота расположения центра тяжести принятого сечения, отсчитанная от произвольной горизонтальной плоскости сравнения;  - потери энергии по тока на преодоление сопротивлений на рассматриваемом участке 1-2. Энергетический смысл уравнения Бернулли заключается в том, что оно выражает закон сохранения механической энергии в жидкости. В 1883 г. английский ученый О. Рейнольдс экспериментально подтвердил существование двух режимов движения реальной жидкости — ламинарного и турбулентного.Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости. Скорость потока, при которой один режим течения переходит в другой, называется критической. Опытным путем установлена связь между диаметром трубы d, в которой движется жидкость с кинематической вязкостью v и критической скоростью wкр:

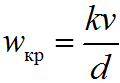
где k — безразмерный эмпирический коэффициент, который на­зывают критическим числом Рейнольдса:

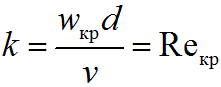
На практике для круглых труб Reкр = 2300. При Re < Reкр имеет место ламинарный поток, при Re > Reкр — турбулентный. Движение потока в закрытых руслах при полном заполнении поперечного сечения жидкостью называется напорным (напри­мер, движение воды в водопроводных трубах). Напорное движе­ние возникает за счет разности давлений в начале и конце трубо­провода. При движении потока возникают потери напора, свя­занные с потерей части энергии на преодоление гидравлических сопротивлений. Гидравлические потери зависят от режима движения жидкости, формы сечения русла и его изменения, харак­тера поверхности стенок и вязкости жидкости. В гидравлике принят способ выражения гидравлических потерь полного напора в линейных единицах (м) и в единицах давления (Па). Решение многих практических задач гидравлики сводится к нахождению зависимости изменения скорости и давления по длине потока. Для этого используют уравнение Бернулли:

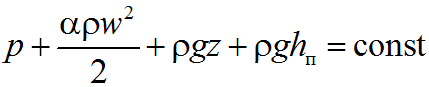
и уравнение постоянства расхода:

Но так как в этих уравнениях три неизвестных (w, р, hп), то для их решения необходимо третье уравнение, кото­рым является зависимость hп = f(w). Суммарные гидравлические потери напора на заданном уча­стке трубопровода равны арифметической сумме местных потерь (сужения, расширения, повороты, задвижки и т.д.) и потерь по длине. Потеря напора в единицах давления выражается формулой

где ?, — суммарный коэффициент местных сопротивлений. Коэффициент местного сопротивления ?, обычно определяют опытным путем. Значения этого коэффициента для различных видов местных сопротивлений приводятся в справочниках по гидравлике.

Основные понятия о жидкости и сжатом воздухе

Жидкости являются телами, которые имеют почти постоянный объем, но не имеют постоянной формы. Жидкости разделяются на вязкие и невязкие. К вязким жидкостям относятся: глицерин, машинное масло, олифа и др. Невязкими и текучими жидкостями являются: вода, бензин, спирт и др. При нагревании жидкости расширяются в объеме: например, вода расширяется на 0,0006, глицерин на 0,0003, керосин на 0,001 своего первоначального объема при повышении температуры на Г. С увеличением давления жидкость незначительно сжимается, т. е. уменьшается в объеме. При давлении в 1 атмосферу вода сжимается на 0,00005 своего первоначального объема. Величина эта так незначительна, что практически можно считать жидкости несжимаемыми. Сжатый воздух, которым пользуются в качестве механической движущей силы для приведения в действие машин, вырабатывается из атмосферного воздуха. Как все газы, так и атмосферный воздух обладает способностью сжиматься. На этом важном свойстве — способности к сжатию атмосферного воздуха — и основан способ получения сжатого воздуха и его применение в промышленности. Сжатие атмосферного воздуха производится особыми машинами, называемыми компрессорами. Существуют компрессоры поршневые и турбинные, резко отличающиеся по своему устройству и принципу работы. Поршневые компрессоры строят одноступенчатыми, двухступенчатыми и многоступенчатыми. Одноступенчатыми они называются потому, что воздух сжимается в них до рабочего давления в 6—7 ат за один прием — одну ступень. В двухступенчатых компрессорах воздух до рабочего давления сжимается в два приема — две ступени. Процесс сжатия воздуха в двухступенчатом компрессоре производится сначала в первом цилиндре до 4 от, а потом через промежуточный охладитель переходит во второй, в котором он подвергается вторичному сжатию до 7 ат. При потреблении сжатого воздуха, превышающего давление 6—7 ат, применяют многоступенчатые компрессоры. Давление в них может быть доведено до 150 ат. Для получения сжатого воздуха высокого давления применяются турбинные компрессоры. Турбинные компрессоры имеют ряд преимуществ перед поршневыми компрессорами, они конструктивно более совершенны, надежны в действии и более компактны. Но турбинные компрессоры более дорогие как по стоимости, так и по эксплуатационным расходам, поэтому они применяются обычно при большом потреблении сжатого воздуха. Атмосферный воздух в компрессорах подвергается сжатию. Степень сжатия зависит исключительно от количества затраченной для этого энергии. Чем больше будет затрачено энергии, тем сильнее будет сжат атмосферный воздух. При сжатии воздух уменьшается в объеме и занимает меньше места: объем сжатого воздуха много меньше объема атмосферного воздуха. Сжатый до определенного давления воздух обладает большой упругостью. Эта упругость сжатого воздуха есть не что иное, как запасенная частицами воздуха энергия давления. Чем больше будет сжат воздух, тем больше, в силу своей упругости, он будет стремиться к расширению. Воздух, освобождаясь от сжатия, стремится к быстрому расширению и этим производит определенную работу. Энергия при превращении в работу широко используется в пневматических инструментах и машинах. Подача сжатого воздуха от компрессоров к необходимым местам производится по трубопроводам.

Основные свойства жидкостей: плотность, удельный вес, вязкость, сжимаемость и др.

Плотность ρ - масса жидкости в единице объема. Для однородной жидкости

ρ=m/V

где  m - масса жидкости в объеме V. Единицы измерения ρ в системе СГС - г/см³, в системе МКГСС - кгс·с²/м⁴, а в системе СИ - кг/м³.

Удельный вес γ - вес жидкости в единице объема:

γ=G/V

где G - вес жидкости. Единицы измерения γ в системе СГС - дин/см³, в системе МКГСС - кгс/м³, а в системе СИ - Н/м³.

Удельный вес и плотность связаны между собой зависимостью γ=ρ·g, где g - ускорение свободного падения.

Плотность и удельный вес некоторых технических жидкостей.

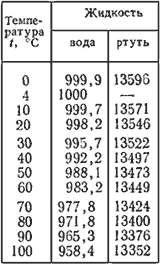
Плотность воды и ртути при разных температурах.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: пуаз, 0,1Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹-10¹² Па·с

Прибор для измерения вязкости называется вискозиметром.

Сила вязкого трения

Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.

Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости.

Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот - под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.

Вторая вязкость

Вторая вязкость, или объёмная вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

Объёмная вязкость играет большую роль в затухании звука и ударных волн, и экспериментально определяется путём измерения этого затухания.

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где  — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность прямо пропорциональна давлению, а - обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов,например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа , растущей с температурой как

Влияние температуры на вязкость газов

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:^[1]

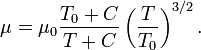
где:

• μ = динамическая вязкость в (Па·с) при заданной температуре T,

• μ₀ = контрольная вязкость в (Па·с) при некоторой контрольной температуре T₀,

• T = заданная температура в Кельвинах,

• T₀ = контрольная температура в Кельвинах,

• C = постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10%, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже

Газ	C [K]	T0 [K]	μ0 [мкПа с]
Воздух	120	291.15	18.27
Азот	111	300.55	17.81
Кислород	127	292.25	20.18
Углекислый газ	240	293.15	14.8
Угарный газ	118	288.15	17.2
Водород	72	293.85	8.76
Аммиак	370	293.15	9.82
Оксид серы(IV)	416	293.65	12.54
Гелий	79.4 [2]	273	19 [3]

См. также [1] (англ.).