7) Обобщенный закон ома для участка цепи с эдс.

Устанавливает связь между напряжениями на участке цепи, ЭДС, действующими на участке, сопротивлениями и током. I=

- суммарное сопротивление участка схемы

ток участка цепи с источниками ЭДС равен алгебраической сумме его напряжения и ЭДС, деленной на сопротивление участка.

8.Метод узловых потенциалов.

Метод узловых потенциалов базируется на законах Ома и Кирхгофа. В левой части уравнения составленных по методу узловых потенциалов записыв-ся произведение потенциала рассм-ого узла на сумму провод-ей ветвей с неизв.токами сходящ.в этом узле в этой же части со знаком минус записыв-ся произведения потенциалов всех узлов,которые соединены с рассмат.узлами ветвями с неизв токами на проводимости этих ветвей.В правой части ток источника причем если он направлен к узлу то +,из узла – и алгебр.сумма произведений ЭДС на проводимость той ветви в которой они наход-ся,если ЭДС направлена к рассматриваемому узлу то произведение со знаком + от то с – Если ток какой-то ветви задан до начала расчета то его можно учитывать как источник,проводимость такой ветви=0 и эту ветвь можно не изображать.Метода расчета эл-ой цепи в котором за неизвестные принимают потенциалы.

9.Линейные соотношения в линейных цепях.

Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной ветви, то две любые величины (токи и напряжения) двух любых ветвей связаны друг с другом линейными зависимостями вида:

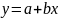
Функцию x выполняет ток или напряжение одной ветви, функцию у - ток или напряжение другой ветви.

ДОКАЗАТЕЛЬСТВО. Согласно методу контурных токов, общее выражение для тока в k-ветви записывается в виде (2.7). Если в схеме изменяется только одна ЭДС, например ЭДС Е_m, то все слагаемые в (2.7), кроме слагаемого 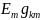, постоянны и могут быть для сокращения записи заменены некоторым слагаемым А_k. Следовательно,

(2.12)

Аналогично, для р-ветви

(2.13)

Найдем Е_m из (2.13):

и подставим в(2.12). Получим

(2.14)

где

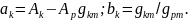
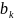Коэффициенты , и , могут быть 0. В частном случае либо , либо может быть равно нулю.

Равенство(2. 14) свидетельствует о том, что при изменении ЭДС Е_m токи I_k и I_р связаны линейной зависимостью. Из теоремы компенсации известно, что любое сопротивление можно заменить источником ЭДС. Следовательно, изменение сопротивления в m-ветви эквивалентно изменению ЭДС Е_m. Таким образом, линейное соотношение между двумя любыми токами (2.14) имеет место при изменении не только ЭДС Е_m, но и сопротивления какой-то m-ветви.

Если обе части (2.12) умножить на сопротивление k-ветви R_k, и проделать аналогичные выкладки, то можно убедиться в том, что напряжение k-ветви линейно связано с током в р-ветви.

Коэффициенты и , из (2.14) и вдругих подобных выражениях могут быть найдены расчетным или опытным путем.

При опытном определении коэффициентов достаточно найти значения двух токов (соответственно напряжений) при двух различных режимах работы схемы и затем решить систему из двух уравнений с двумя неизвестными. Пусть, например, в первом опыте

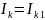и 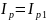, а во втором и .

Тогда

Если в схеме одновременно изменяются ЭДС или сопротивления в каких-либо двух ветвях, то любые три величины в этой схеме (токи, напряжения) связаны друг с другом линейным соотношением Вида .

Доказательство этого соотношения проводится аналогично приведенному ранее.