Izokosta

- všechny kombinace L a K, které mohou být pořízeny za dané celkové náklady

- nákldy TC = wL + rK

w … cena práce (P_L)

L … počet jednotek práce

r … cena kapitálu (P_K)

K … počet jednotek kapitálu

- zvýši-li se cena K – posouváme dolů

- zvýši-li se cena L – posouváme doleva

Mezní míra ekonomické substituce

- poměr, v jakém lze zaměňovat VF při dané úrovni nákladů

- sklon izokosty

- bod, kde se dotýká izokvanta a izokosta

- MRTS = MRES

MRES = =

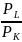16) Optimalizace výroby V dlouhém období (slovně, graficky, matematicky), kapitál a práce V dlouhém období

a) hledáme optimální kombinaci VF, která maximalizuje výstup při daných nákladech

b ) optimální kombinace VF, která minimalizuje náklady za podmínky, že výstup bude mít danou hodnotu

Izokosta

- všechny kombinace L a K, které mohou být pořízeny za dané celkové náklady

Mezní míra ekonomické substituce

- poměr, v jakém lze zaměňovat VF při dané úrovni nákladů

- sklon izokosty

- bod, kde se dotýká izokvanta a izokosta

MRES = = POMĚR V JAKÉM SE MĚNÍ L A K

Kapitál a práce v dlouhém období

- optimální kombinace L a K je tam, kde je izokosta tečnou nejvýše položené izokvanty, resp. izokvanta se dotýká nejníže položené izokosty

17) Náklady V krátkém období, nákladová funkce

Náklady v krátkém období

- celkové náklady STC = FC + VC

- alespoň jeden z VF je fixní (kapitál) – fixní náklady (FC) – neměnné náklady, firma je platí, i když nic nevyrábí

- variabilní náklady (VC) se mění s objemem produkce

- průměrné náklady (AC) jsou náklady, které připadají na jednotku výstupu; průměrné fixní AFC, průměrné variabilní AVC

- mezní náklady (MC) – jak se změní celkové náklady, jestliže se produkce změní o jednotku

SAC = AVC = AFC = SMC =

- AFC s růstem produkce vždy klesají

Průběh nákladové funkce v SR

- závisí na charakteru produkční funkce

- podle toho, jaké výnosy z variabilního vsupu produkce vykazuje, rozlišujeme tři základní situace

• degresivní nákladová funkce – náklady rostou pomaleji než výstup, resp. MC a AC klesají

• progresivní nákladová funkce – náklady rostou rychleji než výstup, resp. MC a AC rostou

• lineární nákladová funkce – náklady rostou stejně jako výstup, resp MC a AC konstantní

• degresivně progresivní nákladová funkce – nejprve rostou náklady pomaleji než výstp, a poté rostou nákaldy rychleji, než výstup; MC protíná AVC a SAC v minimu

TC = wL + rK

18) Náklady V dlouhém období (včetně grafu)

- v LR jsou všechny vstupy variabilní, tudíž FC neexistují

- LTC = VC, FC = 0; neexistují AVC, AFC, pouze LAC

- pro variabilní náklady platí:

• pokud se v produkci prosazují rostoucí výnosy z rozsahu, pak náklady rostou pomaleji než výstup

• pokud se v produkci prosazují klesající výnosy z rozsahu, pak náklady rostou rychleji než výstup

• pokud se v produkci prosazují konstantní výnosy z rozsahu, pak náklady rostou stejným temptem jak výstup

LAC = 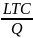náklady, které připadají na jednotku výstupu z dlouhodobého hlediska

L MC = jak se změní dlouhodobé celkové náklady, jestliže se produkce změní o jednotku