6. Матричная формулировка соотношений теории упругости

1. Основные переменные теории упругости

Рассмотрим 3-х мерное тело, нагруженное внешними силами и помещенное в систему координат . Под действием внешних сил тело деформируется. При деформировании произвольная точка g смещается по координатным осям. Компоненты смещения произвольной точки тела в теории упругости обозначают Положительные смещения направлены в положительном направлении координатных осей (рис. 6.1).

Рис. 6.1

Элементарный бесконечно малый объем тела в процессе деформирования всей конструкции изменяет свои линейные размеры и изменяет форму.

Для упрощения рассмотрим процесс изменения размеров и формы на двумерной проекции, исключив третью координату.

Изменение размеров элементарного объема выражается в том, что длины ребер изменяются соответственно на величины , которые называются абсолютными линейными деформациями и положительны при увеличении размеров. В уравнениях удобнее использовать относительные линейные деформации , которые получаются делением соответствующей абсолютной деформации на первоначальный размер (рис. 6.2).

, (6.1)

Рис. 6.2

Изменение формы элементарного объема сводится к тому, что его ребра скашиваются, не приводя при этом к изменению объема (рис. 6.3). Изменение формы описывается тремя переменными , которые показывают, насколько при деформировании изменяются прямые углы между гранями объема. Они называются угловыми деформациями или сдвигами.

Рис. 6.3

Деформации элементарного объема полностью описываются физической величиной, которая называется тензором деформаций и в декартовой системе координат обычно задается квадратной матрицей (6.2), компонентами которой служат перечисленные выше линейные и сдвиговые деформации. Матрица тензора деформаций является симметричной, поскольку .

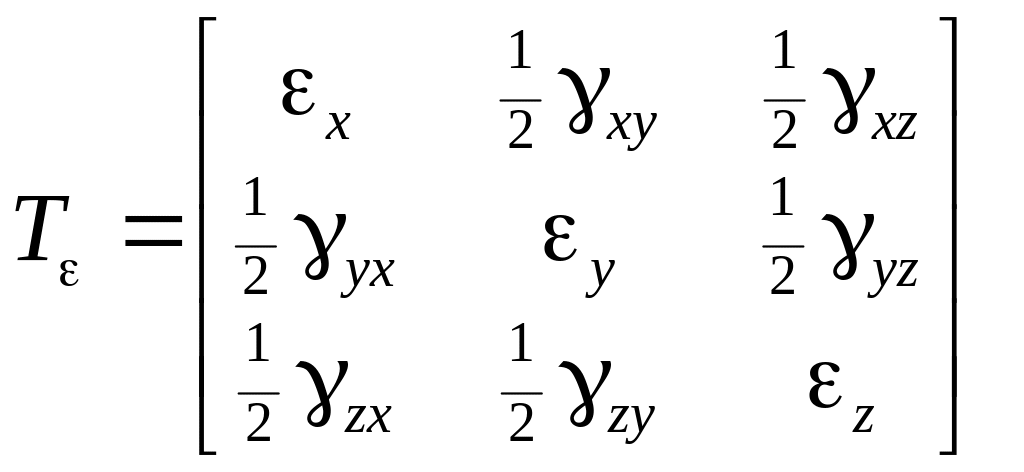(6.2)

Вследствие деформаций тела, в материале конструкции возникают внутренние, распределенные по объему силы, которые называются напряжениями, и фактически представляют собой давление, которое элементарный объем испытывает со стороны остального материала.

Рассмотрим напряжения, действующие на элементарный объем (рис. 6.4). Полные напряжения , действующие на грани объема можно разбить на компоненты по координатным осям, обозначив символом напряжения, перпендикулярные к граням (нормальные напряжения) и символом - напряжения, лежащие в плоскости грани (касательные напряжения). Первый индекс у всех напряжений показывает вдоль какой оси направлена нормаль к той площадке, в которой действует напряжений. Второй индекс у касательных напряжений показывает направление самого вектора.

Рис. 6.4

Напряженное состояние в точке тела полностью описываются физической величиной, которая называется тензором напряжений. Тензор напряжений в декартовой системе координат обычно задается квадратной матрицей (6.3), компонентами которой служат перечисленные выше нормальные и касательные напряжения. Матрица тензора напряжений является симметричной, поскольку в соответствии с законом парности касательных напряжений .

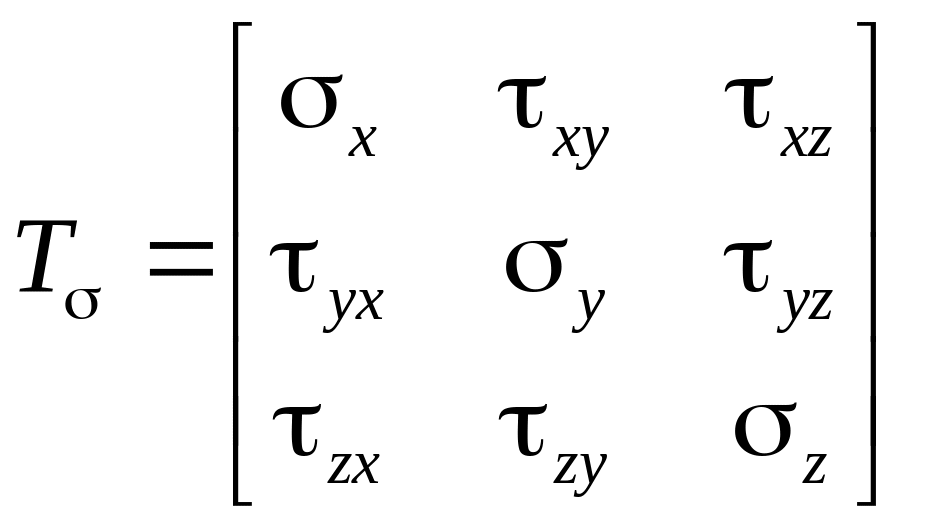(6.3)

Таким образом, видно, что теория упругости оперирует с 15 функциями, каждая из которых, в общем случае, зависит от трех координат.

Смещения	Деформации		Напряжения
	линейные	угловые	нормальные	касательные