Приложение г Лабораторная работа №4

1. изучить теорию по теме лабораторной работы;

2. составить математическую модель по условиям задачи;

3. обработка этой модели методом Франка – Вулфа;

4. обработка этой модели методом штрафных функций;

5. обработка этой модели методом Эрроу – Гурвица;

6. интерпретация полученных результатов, то есть их осмысление в терминах задачи.

Задача № 1. Найти максимальное значение функции f = -x²₁ – x²₂ , при условиях (х₁ – 5)² + (х₂ – 5)² ≤ 8, х₁, х₂ ≥ 0.

Задача № 2. Найти максимальное значение функции f = -x²₁ – x²₂ , при условиях (х₁ – 10)² + (х₂ – 10)² ≤ 21, х₁, х₂ ≥ 0.

Задача № 3. Найти максимальное значение функции f = x²₁ + x²₂ при условиях (х₁ – 4)² - (х₂ – 3)² ≤ 6, х₁, х₂ ≥ 0.

Задача № 4. Найти максимальное значение функции, , при условиях

В качестве начальной точки взять Х⁽⁰⁾=(2;2).

Задача № 5. Найти максимальное значение функции, , при условиях

В качестве начальной точки взять Х⁽⁰⁾=(0, 0, 0).

Задача № 6. Определить наибольшее значение функции , при условии

Задача № 7. Определить наибольшее значение функции , при условии

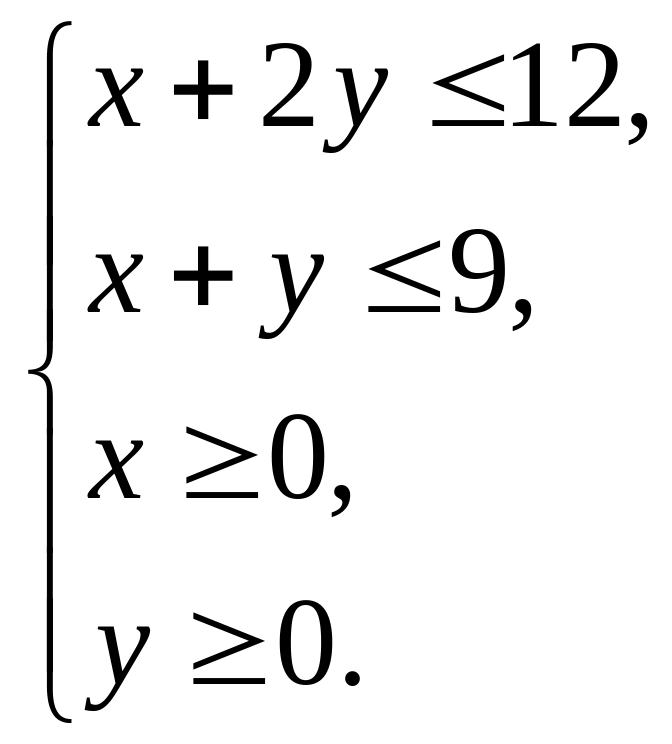
Задача № 8. Определить наибольшее значение функции , при условии

Задача № 9. Найти наибольшее значение функции , при условии

Задача № 10. Найти наибольшее значение функции , при условии

Задача № 11. Найти наибольшее значение функции , при условии

Задача № 12. Найти наибольшее значение функции , при условии

Задача № 13. Найти наибольшее значение функции , при условии

Задача № 14. Найти наибольшее значение функции , при условии

Задача № 15. На производство некоторого продукта расходуется 2 вида ресурсов. Определите оптимальное распределение величин затрачиваемых ресурсов, если цена ресурса первого вида 3 руб, второго 4 руб, а всего выделено на производство 12 руб. Известно, что из количества х₁ первого ресурса и х₂ второго ресурса можно получить единиц продукта.

Г.4 Содержание отчета

Отчет по лабораторной работе должен содержать следующее:

1. название и цель работы;

2. исходные данные задачи;

3. ход решения задачи;

4. результаты расчетов при ручном счете;

5. результаты, полученные программным путем;

6. осмысление полученных результатов в терминах условия задачи;

7. выводы по проделанной работе.

Г.5 Контрольные вопросы

Вопросы для проверки знаний:

1. перечислить наиболее известные градиентные методы;

2. сформулировать определение штрафной функции;

3. записать итерационную формулу метода Франка – Вулфа, штрафных функций и метода Эрроу-Гурвица;

4. сформулировать отличия методов Эрроу-Гурвица и штрафных функций;

5. записать формулу для вычисления числа α_i^(k) в методе Эрроу-Гурвица.

ПРИЛОЖЕНИЕ Д

Лабораторная работа №5

Тема: решение задач динамического программирования.

Цель работы: изучить основные понятия теории динамического программирования, формирование навыков решения задач динамического программирования.

Рекомендации к лабораторной работе:

1. изучить теорию по теме лабораторной работы;

2. составить математическую модель по условиям задачи;

3. обработка этой модели общим методом динамического программирования с учетом особенностей задачи о распределении капиталовложений;

4. интерпретировать полученные результаты, то есть осмыслить их в терминах задачи.