- •Литература
- •Основные понятия теории разностных уравнений
- •2. Стационарные разностные уравнения первого порядка
- •3.Линейные однородные стационарные разностные уравнения второго порядка
- •Линейные неоднородные стационарные разностные уравнения второго порядка
- •Нестационарные линейные разностные уравнения первого порядка
- •Примерная тематика контрольной работы
- •Задания
- •Программные вопросы для подготовки к экзамену:
- •Нестационарные линейные разностные уравнения первого порядка.
- •Примерные варианты тестов
Линейные неоднородные стационарные разностные уравнения второго порядка
Теорема.
Если
- частное решение неоднородного линейного
СРУ, а
 общее
решение соответствующего ему однородного
уравнения, то общее решение неоднородного
ЛСРУ имеет вид:
общее
решение соответствующего ему однородного
уравнения, то общее решение неоднородного
ЛСРУ имеет вид:
 =
=
 ,
,
Пример.
Решим
уравнение
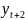 + 9
+ 9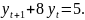
Общее решение соответствующего ему однородного уравнения найдено выше. Предположим, что частное решение данного неоднородного уравнения имеет вид:
= U=const.
Тогда
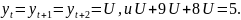
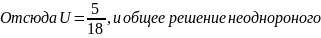 ЛСРУ
найдено:
ЛСРУ
найдено:
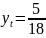 +
+
 +
+
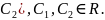
Нестационарные линейные разностные уравнения первого порядка
Рассмотрим уравнение вида
+
 =
=
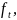 (4)
(4)
где

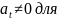 всех
всех
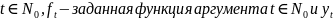 - искомая
функция
- искомая
функция
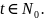
Уравнение (4) – неоднородное линейное разностное нестационарное уравнение первого порядка. Для него имеет место теорема, аналогичная теореме из п. 4.
Пусть
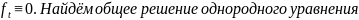
+
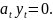 (
(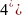
Очевидно,
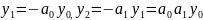 ,
… ,
,
… ,
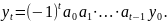
Используя
символ произведения
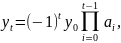
или
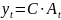 ,
(5)
,
(5)
где
C =
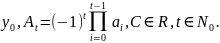
Формула
(5) называется формулой общего
решения уравнения
(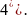
Для решения неоднородного уравнения (4) применим метод вариации постоянной: будем считать С не произвольной постоянной, а некоторой функцией аргумента
Итак, общее решение неоднородного уравнения ищем в виде
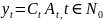 ,
(
,
(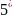 )
)
Подставим ( ) в (4):
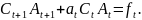
Отсюда
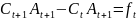
или
 ,
(6)
,
(6)
Поскольку
 для всех
для всех
Из (6) получаем
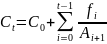
и, следовательно,
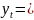 (7)
(7)
Это общее решение линейного неоднородного разностного уравнения первого порядка (4).
Пример.
Решить уравнение
–
 .
.
Решение.
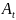 =
=
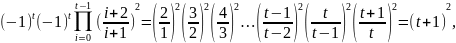
 .
.
Подробнее:
 =
=
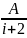 +
+
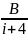 =
=
 .
.
Отсюда 1 = А (i+4) + B(i+ 2).
Если
i =-4, то
1= -2B
и B = - .
.
Если I = - 2, то 1 = 2A и A = .
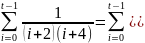 )
=
(
-
)
=
(
-
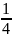 +
+
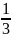 -
-
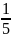 +
-
+
-
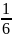 +
+
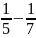 +
+
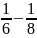 + …
+ …
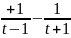 +
+
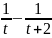 +
+
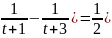 -
-
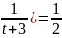
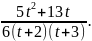
Ответ:
)
Примерная тематика контрольной работы
Определить и обосновать вид дифференциального уравнения (ДУ)1-го порядка. Найти его общее решение и, при наличии начальных условий, также и частное решение.
Решить ДУ 2-го порядка с постоянными коэффициентами.
Найти общее решение стационарного линейного разностного уравнения второго порядка. Найти соответствующее указанным начальным условиям частное решение.
Решить линейное разностное уравнение первого порядка.
Задания
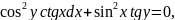
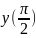 =
0,
=
0,
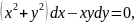

1.2
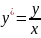 ln
ln ,
,

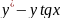 =
=
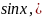 )
)
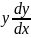 =
=
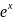 .
.
1.3
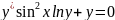 ,
,
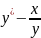 =
,
=
,
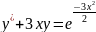 .
.
1.4
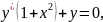
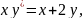

1.5
 (1 +
(1 +
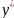 )
)
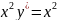 +
+
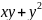 ,
,
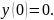
1.6
 (1 +
(1 +
 )
+
)
+
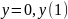 =1,
=1,
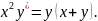
1.7
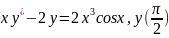 = 0,
= 0,
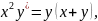
 +
+

1.8
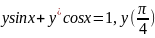 = -
= - ,
,
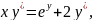
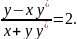
1.9
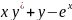 = 0,
= 0,
 = 2,
= 2,


1.10
 +
+
 ,
,
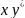 =
=
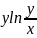 ,
,
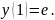
2.
Уравнения |
|
|
|
|||
Параметры |
N |
M |
|
A |
B |
|
Вариант 1 |
4 |
4 |
|
-1 |
1 |
|
Вариант 2 |
2 |
2 |
|
4 |
3 |
|
Вариант 3 |
2 |
1 |
|
3 |
4 |
|
Вариант 4 |
7 |
6 |
|
-6 |
9 |
|
Вариант 5 |
1 |
8 |
|
5 |
-6 |
|
Вариант 6 |
-10 |
25 |
|
1 |
2 |
|
Вариант 7 |
-4 |
5 |
|
8 |
7 |
|
Вариант 8 |
6 |
9 |
|
1 |
1 |
|
Вариант 9 |
-1 |
5 |
|
-5 |
-4 |
|
Вариант 10 |
0 |
5 |
|
3 |
3 |
|
3.
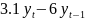 +
9
+
9
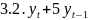 +
6
+
6 = 3,
= 3,
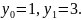
3.3.
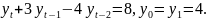
3.4.

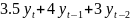 =
2,
=
2,
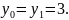
2
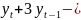 2
2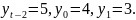
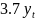 -
4
-
4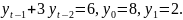
3.
8. 4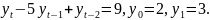
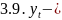 6
6
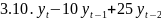 =
8,
=
8,

4.1
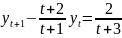 .
4.2
.
4.2
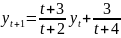 .
.
4.3
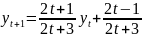 .
4.4
.
4.4
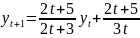 .
.
4.5
=
 .
4.6
.
4.6
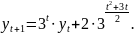
4.7
=
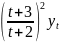
 4.8
=
4.8
=
 .
.
4.9
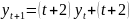 !
4.10
!
4.10
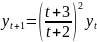 +
+
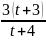 .
.

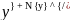 +
+
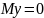
 +
+
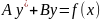
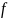 (
(