Лекция № 3. Разностные уравнения
Учебные вопросы
Основные понятия теории разностных уравнений.
Стационарные разностные уравнения первого порядка.
Линейные однородные стационарные разностные уравнения второго порядка.
Линейные неоднородные СРУ второго порядка.
Нестационарные линейные разностные уравнения первого порядка.
Литература
Романко В.К. Разностные уравнения. – М.: Бином, 2006.
Основные понятия теории разностных уравнений
Функция
для значений
переменной
принимает
значения
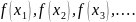
Построим приращения
этой функции при переходе из точки
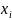в точку
:
=
–
.
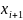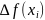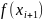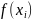(1)
В экономических исследованиях нередко встречаются задачи, в которых роль независимой переменной играет время t, а значения функции фиксируются через равные промежутки времени (1 час, 1 день, 1 месяц, 1 год и т.п.).
Например, так называемая «паутинообразная» модель рынка одного товара описывается уравнением
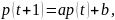(2)
где
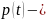цена товара в период времени
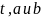- некоторые числа.
При моделировании относительной численности какого-либо биологического вида появляется уравнение вида
),
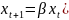(3)
где
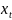- относительная численность популяции
в момент времени t
, а
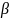- коэффициент размножения.
По аналогии
с (1) построим приращения значений функции
=
……………………..
-
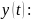
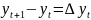
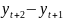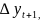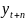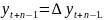(4)
Из системы (4) следует
+
+
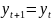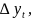
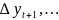
Из определения второй разности следует, что
,
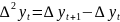или
+
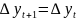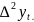
Следовательно,
=
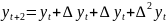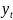+ 2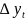
+
Аналогично,
=
+
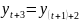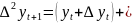+ 2
)
+ (
+
)
=
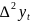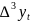+ 3
+ 3
+
.
Используя метод математической индукции, можно доказать, что
=
,
(5)
где
=
.
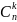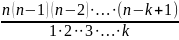Поэтому каждую функцию
можно представить
как функцию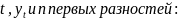
,
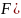t).
Определение.
Уравнение
)
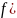= 0
(6)
или
, … ,
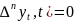(7)
называется разностным уравнением n-го порядка.
Определение.
Решить разностное
уравнение n-го
порядка – значит найти функцию
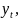для
которой справедливо уравнение вида (6)
или (7).
2. Стационарные разностные уравнения первого порядка
Определение.
Уравнение вида
называется неоднородным стационарным разностным уравнением первого порядка.
Если
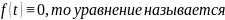однородным.
Обозначим
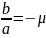и однородное уравнение запишем в виде
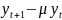= 0.
Отсюда
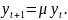
Убедимся в том,
что функция
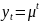является решением этого уравнения:
=
=
).
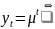
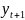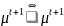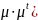Отсюда следует,
что любая функция вида
,
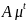где
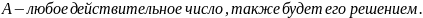
Итак,
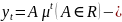общее
решение СРУ I
порядка.
Теорема.
Если
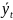- частное решение неоднородного уравнения,
то общее решение неоднородного уравнения
имеет вид
=
+
.
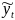Пример.
=
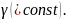
Пусть
=
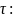
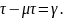Отсюда
=
+
