
- •Лекция 11 Полупроводниковые материалы: Физические свойства, Особенности химической связи
- •Лекция 12 Полупроводниковые материалы
- •Лекция 13 Материалы электронной техники, преобразующие электрические сигналы
- •Лекция 19
- •Теория твердого тела
- •Механизм и кинетика твердофазных реакций
- •Общая характеристика различных типов материалов
- •Современные методы синтеза неорганических материалов с заданной структурой
Лекция 1
Уравнение Шредингера для
идеального кристалла,
Волновая функция электронов в кристалле
Во многом отличия в физико-химических свойствах металлов, полупроводников и диэлектриков в значительной мере обусловлены существованием фундаментальных различий в их зонной структуре, в степени заполнения валентных зон электронами и в значениях ширины разрешенных зон электронов и разделяющих их промежутков (запрещенных зон). Зонная модель твердого тела вытекает из решения уравнения Шредингера для электронов в кристалле. Цель данной лекции, показать, в чем заключается специфика электронной структуры твердых тел, обусловленная их зонным строением и характеризуемая уравнением Шредингера:
Ĥ = Е , (1.1)
где Ĥ – гамильтониан кристалла, - его собственная волновая функция, Е – энергия кристалла.
Волновая функция кристалла зависит от координат всех электронов (ri) и всех ядер (R)
= ( r1, r2, … rn; R1, R2, … Rn ). (1.2)
Гамильтониан включает операторы, характеризующие кинетическую энергию электронов (Ti) и ядер (Tz), потенциальную энергию электронов (Ui) и ядер (Uz), энергию парных взаимодействий электронов и ядер между собой (Uiz)
Ĥ = Ti + Tz + Ui + Uz + Uiz; (1.3)
Ti
=
![]() =
=
 ,
где (1.4)
,
где (1.4)
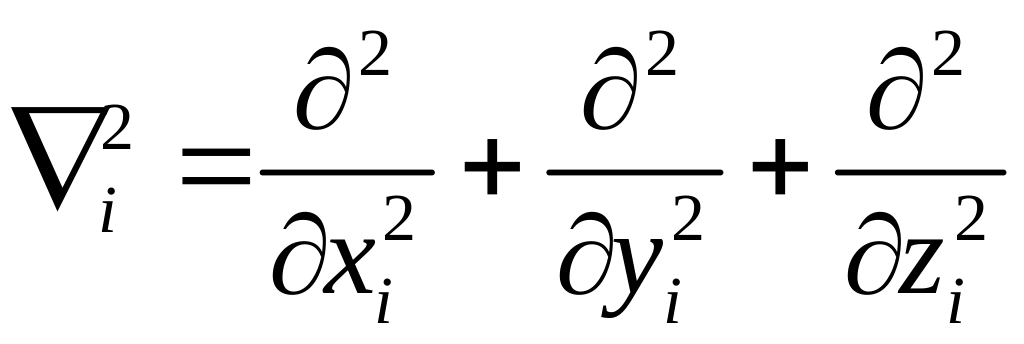 ;
(1.5)
;
(1.5)
Tz
=
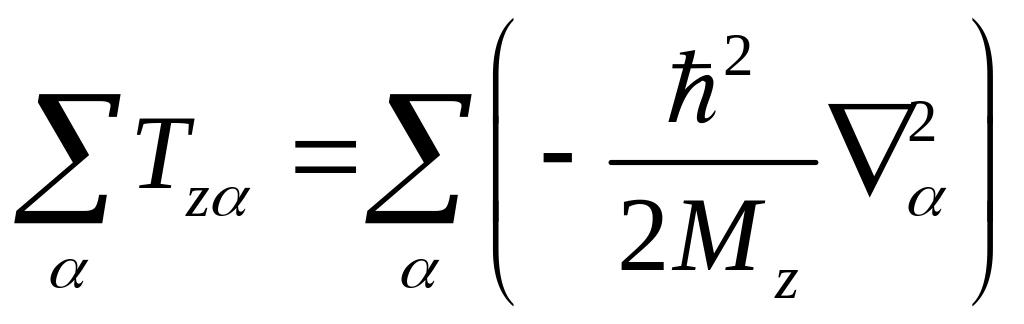 ;
(1.6)
;
(1.6)
Ui
=
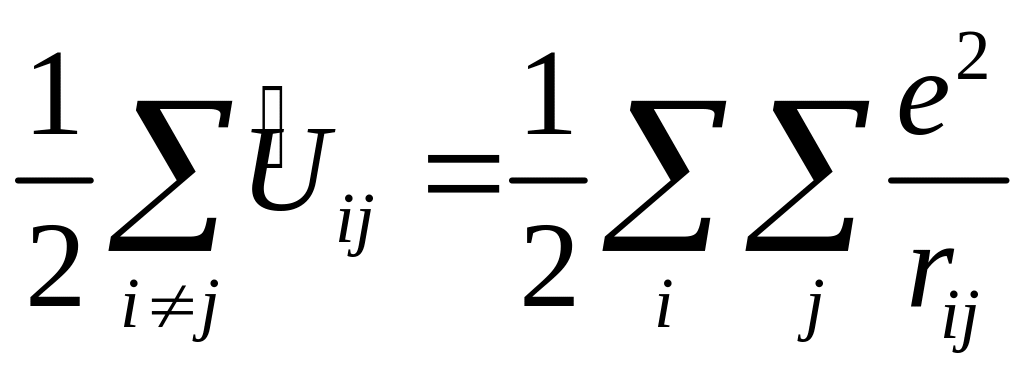 ;
(1.7)
;
(1.7)
Uiz
=
 ;
(1.8)
;
(1.8)
Уравнение с таким гамильтонианом содержит 3N(z+1) переменных, где N – число атомов в кристалле. Учитывая, что в 1 см3 кристалла в среднем содержится 5 1022 атомов, при z = 14 число переменных составляет огромную величину, порядка 2 1024. Очевидно, что решить такое уравнение невозможно, и поэтому вводятся различного рода приближения и, в первую очередь, адиабатическое приближение.
В рамках этого приближения, называемого приближением Борна – Оппенгеймера, кристалл разделяется на две подсистемы – “медленную”, связанную с движением ядер (“тяжелых” частиц) и “быструю” – электронную. Считается, что движение “тяжелого” ядра в силу его инерционности не зависит от движения каждого “легкого” электрона, и поэтому ядро движется в усредненном поле всех электронов. С другой стороны, относительно медленно движущееся ядро увлекает за собой электроны (условие сохранения целостности атомов, составляющих кристалл).
В
простейшем случае принимаем, что ядро
вообще неподвижно, то есть
![]() .
В этом случае кинетическая энергия ядер
.
В этом случае кинетическая энергия ядер
![]() ,
а энергия их взаимодействия между собой
,
а энергия их взаимодействия между собой
![]() ,
которую можно обратить в нуль
соответствующим сдвигом точки отсчета
энергии. В итоге, гамильтониан для
электронов упрощается
,
которую можно обратить в нуль
соответствующим сдвигом точки отсчета
энергии. В итоге, гамильтониан для
электронов упрощается
Ĥ = Ti + Tz + Ui , (1.9)
и уравнение Шредингера приобретает вид:
 ,
(1.10)
,
(1.10)
где
![]() -
координаты покоящихся ядер (параметр,
а не переменная).
-
координаты покоящихся ядер (параметр,
а не переменная).
С целью дальнейшего сокращения числа переменных в уравнении Шредингера принимается, что все электроны, входящие в состав атома, за исключением валентных электронов, вместе с ядром образуют положительно заряженный неподвижный ион (не следует путать с традиционным понятием “ион” в растворах и ионных кристаллах). Эти ионы формируют остов кристалла (“медленную” подсистему), а валентные электроны, соответственно, “быструю” подсистему. Соответственно, в уравнении Шредингера рассматривается движение валентных электронов в потенциальном поле фиксированных ионов (валентная аппроксимация).
Переход
от рассмотрения многоэлектронной
системы к одноэлектронной (с учетом
движения только валентных электронов)
осуществляется в рамках метода
Хартри-Фока, в котором энергия попарного
взаимодействия электронов
![]() заменяется энергией взаимодействия
каждого электрона с усредненным полем
всех остальных электронов:
заменяется энергией взаимодействия
каждого электрона с усредненным полем
всех остальных электронов:
 ,
(1.11)
,
(1.11)
где
![]() - потенциальная энергия отдельно взятого
электрона в поле всех остальных
электронов. В этом соотношении важно,
что двойная сумма (по
- потенциальная энергия отдельно взятого
электрона в поле всех остальных
электронов. В этом соотношении важно,
что двойная сумма (по
![]() и
и
![]() )
заменяется на сумму, каждый из членов
которой зависит от координат одной
частицы. Тогда волновая функция системы
частиц может быть представлена как
произведение волновых функций, описывающих
состояние отдельных частиц системы:
)
заменяется на сумму, каждый из членов
которой зависит от координат одной
частицы. Тогда волновая функция системы
частиц может быть представлена как
произведение волновых функций, описывающих
состояние отдельных частиц системы:
= 123 n , (1.12)
и это означает, что электроны ведут себя независимо друг от друга, а полная энергия системы частиц равна сумме энергий отдельных электронов:
Ee = E1 + E2 + … = Ei. (1.13)
Таким образом, введение самосогласованного поля позволяет рассматривать электроны в кристалле движущимися независимо друг от друга. Это является также и определенным основанием для представления электронов проводимости в виде идеального газа.
Волновая функция электронов в кристалле определяется, в первую очередь, характером взаимодействия валентных электронов с периодическим потенциалом решетки.
Рассмотрим
вид волновой функции электрона,
находящегося в поле с периодическим
потенциалом
![]() кристаллической решетки. Поскольку
точки с радиус-вектором
кристаллической решетки. Поскольку
точки с радиус-вектором
![]() и
и
![]() физически эквивалентны (ввиду наличия
периодичности кристалла:
физически эквивалентны (ввиду наличия
периодичности кристалла:
![]() ),
очевидно, что
),
очевидно, что
![]() .
Соответственно, волновая функция
.
Соответственно, волновая функция
![]() отличается от
отличается от
![]() лишь постоянным множителем:
лишь постоянным множителем:
![]() ,
(1.14)
,
(1.14)
причем
из условия нормировки следует, что
![]() .
.
Из
этого условия можно получить как
тривиальный вывод (![]() ),
так и решение в форме
),
так и решение в форме
![]() .
(1.15)
.
(1.15)
Геометрически такое решение может быть представлено как круговое движение из некоторой произвольной точки по циклической решетке с возвратом в исходную точку. Комбинируя уравнения (1.14) и (1.15), получаем:
![]() .
(1.16)
.
(1.16)
Умножая
правую часть этого уравнения на
exp(ikr)exp(-ikr)
(фактически, на единицу) и комбинируя
экспоненты
![]() и
и
![]() ,
получаем:
,
получаем:
![]() ,
где (1.17)
,
где (1.17)
![]() .
(1.18)
.
(1.18)
Таким образом, волновая функция электрона в кристалле, называемая функцией (или волной) Блоха имеет вид:
![]() ,
(1.19)
,
(1.19)
где
![]() - периодический (с периодом решетки)
множитель, характеризующий взаимодействие
волновой функции электрона с остовами
(ионами) решетки, а
- периодический (с периодом решетки)
множитель, характеризующий взаимодействие
волновой функции электрона с остовами
(ионами) решетки, а
![]() - бегущая плоская волна свободного
электрона с волновым вектором
- бегущая плоская волна свободного
электрона с волновым вектором
![]() в направлении
.
в направлении
.
Лекция 2
ОБРАЗОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ЗОН
В ТВЕРДОМ ТЕЛЕ
Цель данной лекции состоит в объяснении механизма образования энергетических зон в твердом теле, для чего используется два альтернативных подхода – приближение сильно связанных (квазисвязанных) электронов и приближение почти свободных (квазисвободных) электронов.
В рамках приближения сильно связанных электронов принимается, что зонная структура твердого тела образуется в результате уширения энергетических уровней атомов, составляющих кристалл.
Считается, что энергетический спектр изолированного атома нам известен и характеризуется уравнением Шредингера:
![]() ;
(2.1)
;
(2.1)
 ,
(2.2)
,
(2.2)
где
![]() - потенциальная энергия электрона в
изолированном атоме.
- потенциальная энергия электрона в
изолированном атоме.
При
переходе от изолированного атома к
кристаллу в первую очередь необходимо
учесть изменение потенциальной энергии
![]() :
:
![]() .
(2.3)
.
(2.3)
Соответственно, гамильтониан кристалла имеет вид:
Hg = Ha + W (r). (2.4)
С другой стороны, для кристалла волновая функция электрона должна иметь вид блоховской волны:
![]() ,
(2.5)
,
(2.5)
где
![]()
![]() - вектор, соединяющий два соседних атома.
- вектор, соединяющий два соседних атома.
Поскольку для кристалла
![]() ,
(2.6)
,
(2.6)
то с учетом энергии возмущения:
![]() .
(2.7)
.
(2.7)
Так
как не только
![]() ,
но и
,
но и
![]() является собственной функцией
гамильтониана Ha
и, соответственно,
является собственной функцией
гамильтониана Ha
и, соответственно,
![]() ,
(2.8)
,
(2.8)
то уравнение (2.7) упрощается:
![]() .
(2.9)
.
(2.9)
Следуя
стандартным операциям анализа уравнения
Шредингера, умножим выражение (2.9) на
комплексно-сопряженную функцию
![]() ,
где индекс
,
где индекс
![]() означает принадлежность ее к соседнему
атому по сравнению с атомом g,
и проинтегрируем по всему объему
кристалла :
означает принадлежность ее к соседнему
атому по сравнению с атомом g,
и проинтегрируем по всему объему
кристалла :
 .
(2.10)
.
(2.10)
В этом выражении обменный интеграл
![]() (2.11)
(2.11)
характеризует обменную энергию взаимодействия и зависит от степени перекрывания волновых функций атомов и от энергии возмущения.
Второй интеграл:
![]() (2.12)
(2.12)
называется
интегралом неортогональности или
интегралом перекрытия, причем Sgg
= 1 (в этом случае – это просто нормировочный
интеграл для
),
а при
![]() он,
хотя и мал по сравнению с единицей, но
не равен нулю.
он,
хотя и мал по сравнению с единицей, но
не равен нулю.
С учетом введенных обозначений (2.11) и (2.12) уравнение (2.10) можно представить в виде:
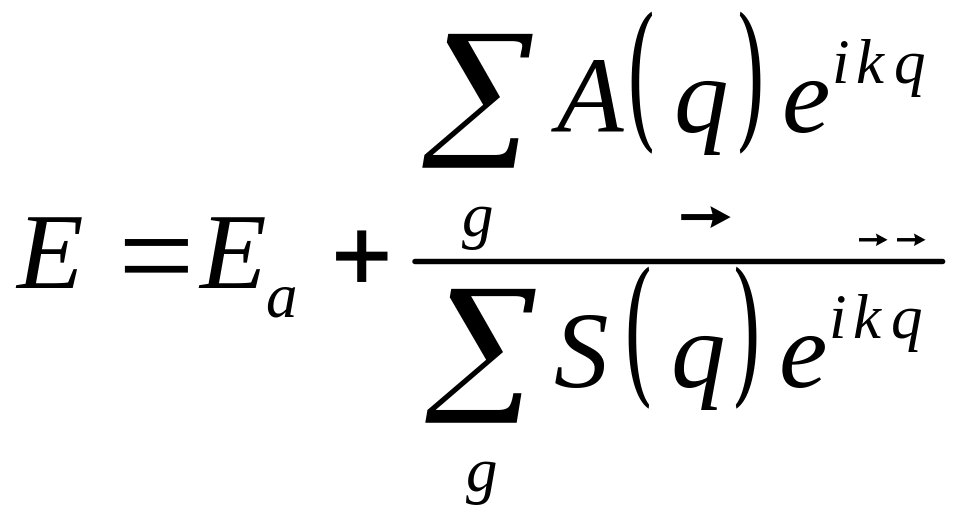 .
(2.13)
.
(2.13)
Поскольку
в приближении сильно связанных электронов
![]() при
при
![]() и
и
![]() при
при
![]() ,
то член в знаменателе
,
то член в знаменателе
![]() .
(2.14)
.
(2.14)
С другой стороны, при для интеграла в числителе можно записать:
 ,
(2.15)
,
(2.15)
где С- константа, не зависящая от . Фактически, С представляет собой усредненную для некоторого атома потенциальную энергию электрона в поле всех остальных ядер с учетом самосогласованного характера поля.
В итоге, уравнение (2.13) приобретает вид:
![]() (2.16)
(2.16)
Рассмотрим
физический смысл этого соотношения на
примере простой кубической ячейки с
периодом
![]() .
Очевидно, что вокруг некоторого
произвольно взятого узла с
соседние узлы будут расположены на
расстоянии
.
Очевидно, что вокруг некоторого
произвольно взятого узла с
соседние узлы будут расположены на
расстоянии
![]() ,
причем у каждого узла будут по шесть
ближайших соседей. В этом случае
,
причем у каждого узла будут по шесть
ближайших соседей. В этом случае
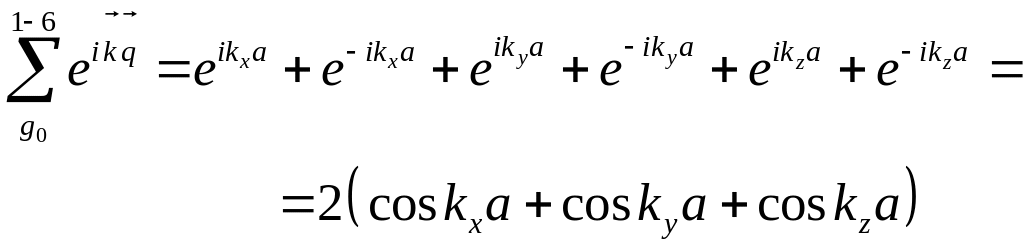 .
(2.17)
.
(2.17)
Соответственно, энергия электрона в периодическом поле прстой кубической решетки равна:
![]() .
(2.18)
.
(2.18)
Очевидно, что экстремальные значения энергии будут иметь место при coskxa = ±1, coskya = ±1, coskza = ±1:
![]() ;
;
![]() ,
(2.19)
,
(2.19)
и, соответственно:
![]() .
(2.20)
.
(2.20)
Из
полученных соотношений следует, что
при образовании кристаллической решетки
в результате взаимодействия атомов
происходит смещение уровня
![]() изолированного атома на величину С.
Одновременно ансамбль атомных уровней
расщепляется в полосу (зону), внутри
которой энергия электронов является
периодической функцией компонентов
волнового вектора
.
Для простой кубической решетки эти зоны
разрешенной энергии имеют ширину 12 А,
то есть определяются величиной обменного
интеграла.
изолированного атома на величину С.
Одновременно ансамбль атомных уровней
расщепляется в полосу (зону), внутри
которой энергия электронов является
периодической функцией компонентов
волнового вектора
.
Для простой кубической решетки эти зоны
разрешенной энергии имеют ширину 12 А,
то есть определяются величиной обменного
интеграла.
Важно, что поскольку величина интеграла есть функция перекрывания электронных облаков соседних атомов, то чем выше степень такого перекрывания, тем шире энергетическая зона разрешенных энергий. Поэтому более высоко расположенные атомные уровни из–за большего перекрывания их волновых функций образуют более широкие энергетические зоны.
Как видно из энергетической диаграммы (рис. 2.1), разрешенные энергетические зоны в общем случае разделены запрещенными интервалами энергий (запрещенными зонами Еg), ширина которых снижается при переходе от внутренних электронных оболочек к наружным. При больших значениях энергии разрешенные зоны могут накладываться (перекрываться).

Рис. 2.1. Образование зонной структуры твердого тела в модели сильно связанных электронов.
Внешние воздействия, вызывающие изменение расстояния между узлами решетки (сжатие или растяжение, нагрев), естественно, приводят к изменению области перекрывания волновых функций, и в результате изменения обменного итеграла вызывают изменение ширины разрешенных и запрещенных зон.
Альтернативой рассмотренной выше модели сильно связанных электронов является модель квазисвободных электронов, в рамках которой принимается, что периодическое поле решеточных остовов действует на валентные электроны лишь как слабое возмущение. Поэтому зависимость энергии электрона от волнового вектора в кристалле аналогична таковой для свободного электрона, то есть соответствует параболическому закону дисперсии:
E = ħ2k2/2m. (2.21)
Однако,
при условии, когда
![]() ,
где
,
где
![]() - целое число, электронная волна
претерпевает брэгговское отражение и,
как результат, резко усиливается ее
взаимодействие с полем периодического
потенциала остовов. Первое отражение
имеет место для
- целое число, электронная волна
претерпевает брэгговское отражение и,
как результат, резко усиливается ее
взаимодействие с полем периодического
потенциала остовов. Первое отражение
имеет место для
![]() ,
второе – для
,
второе – для
![]() и т.д.
и т.д.
Ограничиваясь
рассмотрением первого отражения,
проанализируем вид волновой функции
электрона в кристалле. Наличие брэгговской
дифракции обусловливает то, что при
условии
![]() электронная волна является стоячей.
Существование такой стоячей волны
возможно лишь в том случае, если она
будет состоять из двух бегущих волн
свободного электрона вида
электронная волна является стоячей.
Существование такой стоячей волны
возможно лишь в том случае, если она
будет состоять из двух бегущих волн
свободного электрона вида
![]() и
и
![]() ,
движущихся в противоположных направлениях
( рис. 2.2).
,
движущихся в противоположных направлениях
( рис. 2.2).

Рис. 2.2. Координатная зависимость плотности вероятности ρ для волновых функций Ψ+ и Ψ- в линейном идеальном кристалле.
На основе этих двух бегущих волн можно получить две стоячие волны:
![]() ;
(2.22)
;
(2.22)
![]() .
(2.23)
.
(2.23)
Из формулы Эйлера следует, что:
![]() ;
(2.24)
;
(2.24)
![]() .
(2.25)
.
(2.25)
В уравнениях (2.22) – (2.25) знак пропорциональности вместо знака равенства стоит из–за того, что для упрощения не вводится условие нормировки.
Для определения координатной зависимости плотности заряда ρ (определяющей, фактически, координатное положение электронов) найдем квадрат модуля волновых функций (2.24) и (2.25):
![]() ;
(2.26)
;
(2.26)
![]() .
(2.27)
.
(2.27)
Из
этих соотношений видно, что электроны
могут располагаться в линейном кристалле
двумя разными способами: в областях,
где потенциальная энергия минимальна
![]() ,
то есть непосредственно на положительных
ионах (функция
,
то есть непосредственно на положительных
ионах (функция
![]() ),
и в промежутках, точно посередине между
остовами (функция
),
и в промежутках, точно посередине между
остовами (функция
![]() ),
что показано на рис. 2.2.
),
что показано на рис. 2.2.
Таким образом, волновая функция Ψ+, давая максимумы плотности заряда вблизи положительных ионов, понижает потенциальную энергию относительно ее среднего уровня, а функция Ψ-, напротив, ее повышает. В результате, средние значения потенциальной энергии для функций ρ+ и ρ- различаются на некоторую величину (энергетическую щель), называемую запрещенной зоной с шириной, обозначаемой Eg (рис. 2.3).

Рис. 2.3. Зависимость энергии от волнового вектора для свободного электрона (а) и для электрона в решетке (б).
Лекция 3
Энергетическое распределение электронов в кристалле; зоны Бриллюэна
Идеальный кристалл бесконечен, состоит из элементарных ячеек, заполняющих без промежутков все его пространство, и обладает регулярной периодической структурой. Кристаллическая решетка - совокупность точек (узлов), связанных тремя некомпланарными векторами трансляций a, b, c:
T = n1a + n2b + n3c, (3.1)
где n1, n2, n3 - целые числа.
В частном случае решетка может быть двумерной либо одномерной, характеризуемой двумя либо одним базисным вектором, соответственно. Параллелепипеды (для трехмерной решетки) и параллелограммы (для двумерной), построенные на векторах трансляции образуют элементарную ячейку решетки, причем для удобства используется комбинация наиболее коротких векторов. В ряде случаев целесообразно построение элементарной ячейки таким образом, чтобы она охватывала область пространства, которая была бы ближе к данному узлу, чем к любому другому трансляционно-эквивалентному узлу (ячейка Вигнера-Зейтца) - рис. 3.1.
Для этого необходимо выбрать некоторый узел (далее он считается центральным) и соединить его линиями со всеми соседними узлами. Перпендикулярные плоскости, проведенные через середины соединяющих отрезков, образуют ячейку Вигнера-Зейтца (рис. 3.1). Такая ячейка имеет ту же точечную симметрию, что и решетка Браве кристалла, и, естественно, при трансляции заполняет все пространство кристалла без промежутков.

Рис. 3.1. Ячейка Вигнера-Зейтца для квадратной, треугольной и кубической решеток.
Если
кристаллическую точечную решетку
представить в виде
![]() (
(
![]() - вектора элементарной ячейки,
- вектора элементарной ячейки,
![]() - целые числа ), то обратная решетка будет
иметь вид:
- целые числа ), то обратная решетка будет
иметь вид:
![]() ,
(3.2)
,
(3.2)
где
![]() - целые числа, а векторы
- целые числа, а векторы
![]() находятся из соотношений:
находятся из соотношений:
 (3.3)
(3.3)
Таким
образом, векторы
- это основные векторы обратной решетки.
В соотношения типа (3.3) кристаллографы
обычно опускают множитель
![]() ,
но в теории твердого тела он используется
по аналогии с множителем
при переходе от обычной частоты к
круговой (
,
но в теории твердого тела он используется
по аналогии с множителем
при переходе от обычной частоты к
круговой (![]() ).
).
Переход от кристаллической решетки к обратной имеет достаточно сложный физический смысл – фактически мы переходим к пространству частот (величина a-1 характеризует пространственную частоту решетки).
Таким образом, кристалл может быть охарактеризован частотным параметром (вектором обратной решетки – так называемым k-вектором, равным k = 2π/λ, и обозначающим число волн, укладывающихся на длине 2π, см). Очевидно, что для двух- и трехмерного кристалла пространственные частоты по разным направлениям могут быть различными.
Для рассмотрения состояния электронов в реальном кристалле необходимо найти способ учета его конечных размеров, то есть ввести определенные граничные условия. Чтобы устранить нарушение трансляционной симметрии на краях кристалла и ограничить число структурных единиц в нем можно использовать циклические граничные условия Борна-Кармана. В частности, для ограниченного кристалла в форме параллелепипеда с размерами по осям x, y, z равными, соответственно, Lx, Ly, Lz, составленного из элементарных кубических ячеек можно записать:
Lx = aNx; Ly = aNy; Lz = aNz, (3.4)
где Nx, Ny, Nz - число атомов, укладывающихся на каждом из ребер кристалла. Задавая тождественность волновой функции на противоположных гранях параллелепипеда, получаем граничные условия цикличности Борна-Кармана:
Ψ (x, y, z) = Ψ (x + Lx, y + Ly, z+ Lz). (3.5)
Учитывая, что волновая функция электрона в кристалле имеет вид волны Блоха, для выполнения данных условий цикличности необходимо принять, что:
exp(ikxLx) = exp(ikyLy) = exp(ikzLz) = 1. (3.6)
Такое равенство имеет место при условии, что показатель экспоненты является целым числом, умноженным на 2πi, то есть:
kxLx = 2πn1, kyLy = 2πn2, kzLz = 2πn3, (3.7)
где n1, n2, n3, - целые произвольные числа. Из этого следует, что
kx = 2πn1/Lx, ky = 2πn2/Ly, kz = 2πn3/Lx. (3.8)
Из соотношения (3.8) видно, что компоненты волнового вектора k изменяются не непрерывно, а принимают ряд дискретных значений. Принимая во внимание, что Lx = aNx, можно заключить, что компонента kx имеет Nx значений, соответствующих различным значениям n1, причем оно изменяется в пределах
0 ≤ n1 < Nx или -Nx/2 ≤ n1 < Nx/2. (3.9)
Из этих соотношений вытекает, что компоненты вектора k существуют в следующих интервалах:
-π/a ≤ kx < π/a, -π/a ≤ ky < π/a, -π/a ≤ kz < π/a, (3.10)
где kx , ky , kz принимают соответственно Nx, Ny, Nz различных значений.
Таким образом, в рассматриваемой квантовохимической системе содержится всего N = NxNyNz = LxLyLz/a3 различных компонентов вектора k, равное числу элементарных ячеек в кристалле. Это, в принципе, означает, что если каждому значению вектора k будет сопоставлено определенное значение энергии электрона, то в простой энергетической зоне, возникшей из невырожденного атомного уровня, имеется 2N квантовых состояний, и, соответственно N энергетических уровней.
Фактически, компоненты k - вектора kx, ky, kz являются тремя квантовыми числами, а четвертым квантовым числом является спиновое число – sz. Поскольку проекция sz может принимать только два значения +1/2 и -1/2, понятно, что в состоянии с одним набором трех компонентов kx , ky , kz может быть не более двух электронов.
Состояние электрона, свободно движущегося в пространстве, характеризуется энергией E и импульсом P, причем E = P2 / 2m как и в ньютоновской механике.
С другой стороны, длина волны де Бройля равна λ = h / P, где h - постоянная Планка. Учитывая, что P = mv, а k = 2π / λ, получаем, что импульс электрона P = ħk, где ħ = h / 2π, а энергия E = ħ2k2 / 2m.
Для электрона, движущегося в периодическом поле кристалла, понятие импульса существенно изменяется, поскольку параметры движения становятся сильно зависящими от воздействия периодического потенциала остовных ионов. В связи с этим вводится понятие квазиимпульса p = ħk, который квантован в соответствии с дискретным спектром волнового вектора k.
Таким образом, в энергетической зоне кристалла имеется N энергетических состояний, которым соответствуют значения компонент волнового вектора ki = 2πnj / Li и компонент квазиимпульса pi = 2πħnj / Li , где i = x, y, z, а j = 1, 2, 3.
Для кристалла с простой кубической решеткой достаточно рассматривать изменение компонентов ki и pi в пределах -π/a ≤ ki < π/a и -πħ/a ≤ pi < πħ/a. Этим значениям квазиимпульса в системе координат px, py, pz будет соответствовать некоторая область, построенная вокруг начала координат и содержащая все возможные различные состояния. Эта область называется первой (основной) зоной Бриллюэна. Ее можно также определить как ячейку Вигнера-Зейтца в обратной решетке.
В заключение этого раздела рассмотрим кратко основные принципы расчета электронной структуры твердых тел.
Для решения уравнения Шредингера, описывающего состояние электронов в твердом теле, его можно разложить в ряд по полной системе функций, удовлетворяющих тем же граничным условиям, что и искомое решение, причем в упрощенном варианте можно ограничиться конечным набором этих функций:
 .
(3.11)
.
(3.11)
Учитывая, что волновая функция электрона в кристалле (функция Блоха) вблизи атомных остовов ведет себя подобно атомной функции , а на удалении от остовов, как набор плоских волн , для разложения уравнения Шредингера можно использовать как сферические волны , так и плоские волны .
В первом случае методы расчета зонной структуры твердого тела относят к методам ячеек, во втором – к вариационным методам.
Лекция 4
ЗОННОЕ СТРОЕНИЕ ДИЭЛЕКТРИКОВ, ПОЛУПРОВОДНИКОВ, МЕТАЛЛОВ; статистика электронов и дырок в твердом теле
Если валентные электроны заполняют целиком одну или более верхних разрешенных зон, то кристалл при абсолютном нуле является диэлектриком. Если к нему приложить электрическое поле, то потока электронов не будет и, если целиком заполненная зона отделена от следующей более высокой зоны энергетической щелью, то непрерывного способа изменить суммарный импульс электронов не существует – необходимо приложение энергии не меньшей, чем Eg.
В диэлектриках число возможных состояний в валентной зоне равно количеству валентных электронов атомов, образовавших кристалл. В этом случае на каждом уровне находятся по два электрона с противоположно направленными спинами. Примером такой ситуации является кристалл хлорида натрия, в котором валентная зона образована преимущественно ионами хлора Cl- (3s23p6), у которых все 6N состояний заняты электронами. Зона проводимости у NaCl образована ионами Na+ (1s22s22p6) и является полностью пустой. Расстояние между ними так велико (Eg ~ 7 эВ), что NaCl является типичным диэлектриком (рис. 4.1а).

Рис. 4.1. Типичные зонные диаграммы диэлектрика (а), полупроводника (б), металла с «перекрытием зон» (в) и с частичным заполнение зоны проводимости (г)
В целом подобное энергетическое строение характерно и для полупроводников, с тем отличием, что ширина запрещенной зоны у них меньше, и составляет величину от десятых-сотых долей эВ до 3 эВ.
Зонное строение металлов может быть охарактеризовано двумя крайними типами структур: первый тип – с частичным заполнением электронами валентной зоны (рис. 4.1в), а второй – с перекрытием зон (рис. 4.1б). К первому типу можно отнести щелочные металлы, благородные металлы, медь и др. Например, у натрия (1s22s22p63s1) зоны, образованные из уровней 1s, 2s и 2p, полностью заполнены, а в зоне валентных электронов, образованной из уровня 3s, в 2N состояниях находится N электронов, которые заполняют энергетическую зону лишь наполовину.
У металлов второй группы реализуется иная ситуация – в валентной зоне все возможные электронные состояния заняты, но эта зона перекрывается со свободной зоной, не занятой электронами. Например, несмотря на то, что у магния (1s22s22p63s2) 3s-зона полностью занята, она перекрывается с Зр-зоной, и магний проявляет металлические свойства.
Электроны, характеризуясь спином 1/2, подчиняются статистике Ферми – Дирака:
 ,
(4.1)
,
(4.1)
где
![]() - вероятность заполнения состояния с
энергией
- вероятность заполнения состояния с
энергией
![]() электроном при температуре T;
F
– уровни Ферми (электрохимический
потенциал) – приращение свободной
энергии системы при добавлении к ней
электрона в изобарно-изотермических
условиях.
электроном при температуре T;
F
– уровни Ферми (электрохимический
потенциал) – приращение свободной
энергии системы при добавлении к ней
электрона в изобарно-изотермических
условиях.
С другой стороны, уровень Ферми – энергетический уровень, ниже которого все состояния системы частиц или квазичастиц, подчиняющихся статистике Ферми – Дирака, заполнены, а выше – пусты в основном состоянии при Т = 0 К. При Т 0 – уровень Ферми характеризуется вероятностью заполнения, равной 0.5 при любой температуре.
Поскольку функция Ферми – Дирака (4.1) характеризует вероятность заполнения электроном данного квантового состояния, вероятность того, что электрон отсутствует (состояние занято дыркой), равна:
 .
(4.2)
.
(4.2)
Как видно из этого соотношения, функция распределения дырок аналогична таковой для электронов, с тем отличием, что отсчет энергии ведется от потолка валентной зоны.
Лекция 5
КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
Наряду с электронной подсистемой, поведение твердых тел в различного рода химических, термо-, фотохимических и других процессах определяется колебательной, или фононной, подсистемой. Колебания решетки – согласованные колебательные смещения структурных элементов кристалла относительно их положений равновесия. Если амплитуда колебаний намного меньше постоянной решетки, колебания являются гармоническими (нормальными), с видом плоской волны, характеризующейся волновым вектором . Квант энергии колебания решетки называется фононом.
В
трехмерной решетке смещения атомов
можно описать как суперпозицию нормальных
колебаний, каждое из которых характеризуется
своим
- вектором, длиной волны
либо частотой
![]() .
Волновой
- вектор имеет столько разрешенных
значений, сколько в кристалле содержится
элементарных ячеек, и изменяется в
пределах зоны Бриллюэна
.
Волновой
- вектор имеет столько разрешенных
значений, сколько в кристалле содержится
элементарных ячеек, и изменяется в
пределах зоны Бриллюэна
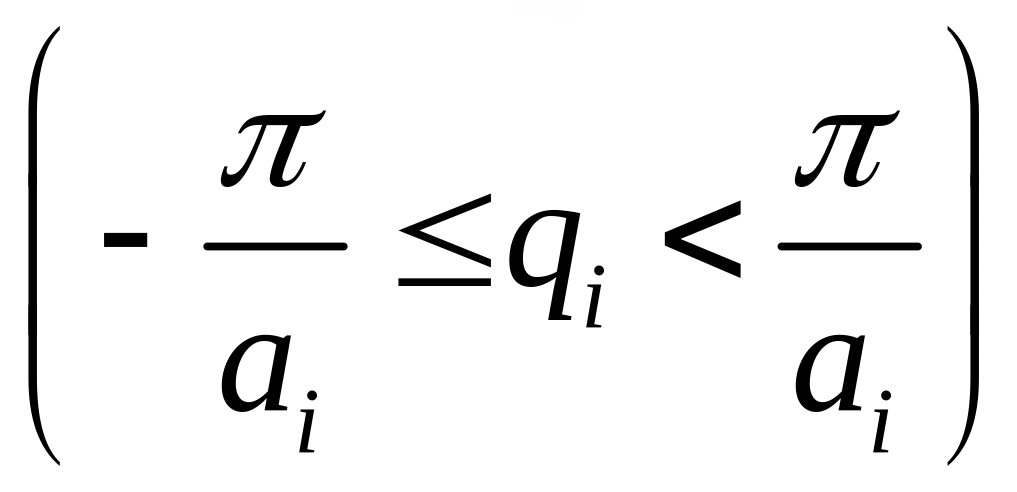 ,
где
,
где
![]() - постоянная решетки,
- постоянная решетки,
![]() .
Поскольку каждый атом обладает тремя
степенями свободы, то общее чис
.
Поскольку каждый атом обладает тремя
степенями свободы, то общее чис![]() ло
степеней свободы в кристалле равно
ло
степеней свободы в кристалле равно
![]() ,
где
,
где
![]() -
число атомов в одной элементарной
ячейке,
-
число атомов в одной элементарной
ячейке,
![]() -
число элементарных ячеек в кристалле.
Именно это же количество (
)
волн и содержится в кристалле. Если
учесть, что каждая из этих волн может
быть представлена как гармонический
осциллятор с энергией
-
число элементарных ячеек в кристалле.
Именно это же количество (
)
волн и содержится в кристалле. Если
учесть, что каждая из этих волн может
быть представлена как гармонический
осциллятор с энергией
![]()
 ,
(5.1)
,
(5.1)
где
![]()
![]() - энергия нулевых колебаний, то полная
энергия колебаний в кристалле равна:
- энергия нулевых колебаний, то полная
энергия колебаний в кристалле равна:
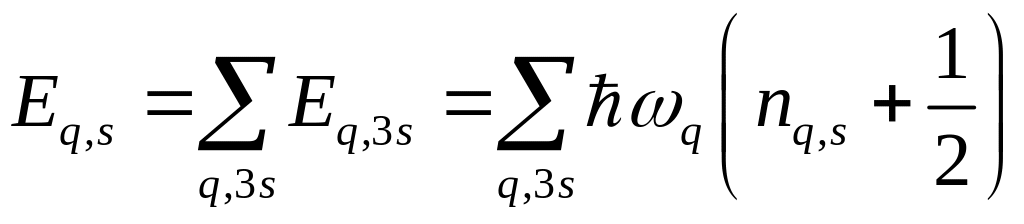 .
(5.2)
.
(5.2)
Квантовый
осциллятор с энергией
![]() (уравнение 5.2) может изменять свою энергию
на величину
(уравнение 5.2) может изменять свою энергию
на величину
![]() ,
где . Соответствующий квант энергии
колебаний решетки – фонон, равен
,
причем процесс с
,
где . Соответствующий квант энергии
колебаний решетки – фонон, равен
,
причем процесс с
![]() означает рождение фонона, а с
означает рождение фонона, а с
![]() - его уничтожение. Фактически, фонон
можно рассматривать как единичное
квантовое возбуждение определенного
нормального колебания. По аналогии с
фотоном, фонон также можно представить
как носитель кванта энергии колебаний
решетки, то есть как квазичастицу (в
рамках гипотезы корпускулярно –
волнового дуализма).
- его уничтожение. Фактически, фонон
можно рассматривать как единичное
квантовое возбуждение определенного
нормального колебания. По аналогии с
фотоном, фонон также можно представить
как носитель кванта энергии колебаний
решетки, то есть как квазичастицу (в
рамках гипотезы корпускулярно –
волнового дуализма).
Фононы подчиняются статистике Бозе-Эйнштейна:
 ,
(5.3)
,
(5.3)
где
![]() - среднее число фононов в данном нормальном
колебании с энергией фононов
в условиях теплового равновесия,
- среднее число фононов в данном нормальном
колебании с энергией фононов
в условиях теплового равновесия,
![]() - постоянная Больцмана.
- постоянная Больцмана.
Поскольку
в приближении гармонических колебаний
колебательная часть энергии кристалла
равна аддитивной сумме энергий фононов
![]() ,
колебательное состояние кристалла
может быть представлено как “идеальный
газ фононов” (квазичастиц, не
взаимодействующих друг с другом).
,
колебательное состояние кристалла
может быть представлено как “идеальный
газ фононов” (квазичастиц, не
взаимодействующих друг с другом).
На основании распределения Бозе – Эйнштейна (5.3) можно полагать, что при Т = 0 К концентрация фононов в кристалле должна быть нулевой. Однако, в действительности, квантовая природа колебаний решетки обуславливает существование “нулевых колебаний” атомов даже при Т = 0 К. В частности, в кристалле гелия “нулевые колебания” приводят к тому, что твердый кристаллический гелий при Т 0 К существует лишь при давлении, превышающем 25 атм. При снижении давления он плавится, превращаясь в так называемую квантовую жидкость. В целом же, очевидно, что амплитуда колебаний при сверхнизких температурах незначительна, хотя и отлична от нуля.
При![]() фононный газ заключает в себе практически
основную часть тепловой энергии
кристалла. В окрестностях этого
температурного диапазона имеет место
близкий к линейному рост числа фононов
с увеличением температуры. Этим
обстоятельством можно объяснить
известное эмпирическое правило Дюлонга
и Пти, согласно которому молярная
теплоемкость при постоянном объеме для
всех простых тел одинакова и приблизительно
равна 25 Дж/мольК.
Действительно, учитывая, что число
колебательных степеней свободы у
кристалла равно
фононный газ заключает в себе практически
основную часть тепловой энергии
кристалла. В окрестностях этого
температурного диапазона имеет место
близкий к линейному рост числа фононов
с увеличением температуры. Этим
обстоятельством можно объяснить
известное эмпирическое правило Дюлонга
и Пти, согласно которому молярная
теплоемкость при постоянном объеме для
всех простых тел одинакова и приблизительно
равна 25 Дж/мольК.
Действительно, учитывая, что число
колебательных степеней свободы у
кристалла равно
![]() (
(![]() - число Авогадро), средняя энергия
теплового движения на 1 моль вещества
составляет
- число Авогадро), средняя энергия
теплового движения на 1 моль вещества
составляет
![]() ,
а соответствующая мольная теплоемкость
равна
,
а соответствующая мольная теплоемкость
равна
![]() Дж/мольК.
Дж/мольК.
При
понижении температуры теплоемкость
падает гораздо ниже того значения,
которое дает правило Дюлонга и Пти,
устремляясь к нулю, как функция Т3
для диэлектриков, и линейно снижается
с температурой для металлов. Правило
Дюлонга и Пти справедливо для температуры
выше
![]() - температуры Дебая (характеристической
температуры в твердом теле, вводимой
соотношением
- температуры Дебая (характеристической
температуры в твердом теле, вводимой
соотношением
![]() ,
где
,
где
![]() - максимальная частота колебаний
кристаллической решетки, определяемая
из условия равенства числа колебаний,
приходящихся на частотный интервал от
0 до
,
полному числу колебательных степеней
свободы решетки), когда возбуждены все
колебательные степени свободы. При
- максимальная частота колебаний
кристаллической решетки, определяемая
из условия равенства числа колебаний,
приходящихся на частотный интервал от
0 до
,
полному числу колебательных степеней
свободы решетки), когда возбуждены все
колебательные степени свободы. При
![]() имеет место “вымораживание” все
большего числа степеней свободы и,
соответственно, снижение
имеет место “вымораживание” все
большего числа степеней свободы и,
соответственно, снижение
![]() .
Вследствие этого для таких материалов,
как алмаз (
.
Вследствие этого для таких материалов,
как алмаз (![]() )
и бериллий (
)
и бериллий (![]() )
значения
существенно ниже предсказываемых
правилом Дюлонга и Пти даже при комнатной
температуре.
)
значения
существенно ниже предсказываемых
правилом Дюлонга и Пти даже при комнатной
температуре.
Максимальная
энергия фононов имеет величину порядка
![]() ,
а минимальная длина волны
,
а минимальная длина волны
![]() фонона соответствует наибольшему
значению волнового числа
фонона соответствует наибольшему
значению волнового числа
![]() .
В простейшем случае дискретной одномерной
цепочки атомов очевидно, что
.
В простейшем случае дискретной одномерной
цепочки атомов очевидно, что
![]() ,
поскольку, естественно, что в дискретной
цепочке не могут существовать волны с
длиной полуволны меньшей, чем период
решетки. В результате, для колебаний
дискретных атомных структур характерно
наличие предельной частоты
,
поскольку, естественно, что в дискретной
цепочке не могут существовать волны с
длиной полуволны меньшей, чем период
решетки. В результате, для колебаний
дискретных атомных структур характерно
наличие предельной частоты
![]() фононов. Поскольку в твердых телах
скорость звука
фононов. Поскольку в твердых телах
скорость звука
![]() см/с,
см/с,
![]() 310-8
см, предельная частота фононов
310-8
см, предельная частота фононов
![]() - величина порядка 21013
Гц.
- величина порядка 21013
Гц.
В
трехмерном кристалле имеется два типа
упругих волн: продольные (деформация
сжатия – растяжения) и поперечные
(деформация сдвига). Очевидно, что
поперечные волны в каждой плоскости
имеют два главных направления, поскольку
эти колебания можно разложить на две
независимые поперечные волны со взаимно
перпендикулярными направлениями. В
итоге, кристалл, содержащий
атомов в элементарной ячейке,
характеризуется наличием
![]() типов поперечных волн и
типов продольных волн, то есть суммарно
наличием
типов поперечных волн и
типов продольных волн, то есть суммарно
наличием
![]() различных типов (ветвей) колебаний.
различных типов (ветвей) колебаний.
Три
ветви колебаний, для которых фазовая
скорость равна групповой скорости и
равна скорости звука, называются
акустическими. Для них частота продольных
колебаний выше, чем частота поперечных.
Остальные
![]() ветви называются оптическими, для
которых при
ветви называются оптическими, для
которых при
![]() фазовая скорость стремится к бесконечности,
а групповая – к нулю.
фазовая скорость стремится к бесконечности,
а групповая – к нулю.
Графически
акустические и оптические фононы в
приближении
для цепочечного кристалла с
![]() представлены на рис. 5.1. Как видно из
рисунка, оптические фононы обусловлены
встречным колебательным движением
атомов двух сортов (“черные” и “белые”).
Очевидно, что если эти атомы различаются
по своему электрическому заряду, то
изменение расстояния между ними будет
приводить к изменению дипольного
момента, что в свою очередь может
проявляться в поглощении и испускании
ИК – излучения. Поэтому такого типа
колебания были названы оптическими.
представлены на рис. 5.1. Как видно из
рисунка, оптические фононы обусловлены
встречным колебательным движением
атомов двух сортов (“черные” и “белые”).
Очевидно, что если эти атомы различаются
по своему электрическому заряду, то
изменение расстояния между ними будет
приводить к изменению дипольного
момента, что в свою очередь может
проявляться в поглощении и испускании
ИК – излучения. Поэтому такого типа
колебания были названы оптическими.
Для примера на рис. 5.1 приведены дисперсионные кривые (зависимость фононной частоты от волнового вектора ) для кристаллов кремния. Поскольку в ячейке Вигнера – Зейтца кремния имеется два атома, эти кривые содержат как акустические, так и оптические ветви (LA – продольная акустическая, LO – продольная оптическая, TA – поперечная акустическая, TO – поперечная оптическая).

Рис. 5.1 . Колебания узлов решетки, обусловливающие возникновение акустических (а) и оптических (б) фононов; типичные дисперсионные кривые для фононов (в)
Количество ветвей определяется наличием трех продольных акустических (по трем осям), трех продольных оптических, и в два раза больше поперечных (связанных с деформацией сдвига во взаимно перпендикулярных направлениях в каждой из трех плоскостей) акустических и оптических фононов. Однако ввиду наличия достаточно высокой симметрии у кристалла, часть колебаний оказывается вырожденной, а на дисперсионной кривой в кристаллографическом направлении 100 видны ветви ТО и ТА (обе дважды вырожденные), LO и LA. Характерно, что на краях зоны Бриллюэна, то есть когда , различия между оптическими и акустическими колебаниями минимальны.
Для определения параметров фононного спектра используются методы поглощения нейтронов либо фотонов. При поглощении фотонов (в ИК области), обычно, происходит резонансное превращение фотона в оптический фонон, причем на спектре поглощения обычно регистрируются комбинационные частоты (LO + TA, TO + LO и др.).
Фононы в твердых телах могут взаимодействовать как между собой, так и с другими квазичастицами, а также с дефектами кристаллической решетки. Взаимодействие фононов между собой можно рассматривать как проявление ангармонизма колебаний, приводящего к рождению новых фононов, либо напротив, к их аннигиляции, рассеянию друг на друге с изменением частоты и поляризации. Такого рода взаимодействия объясняют факт теплового расширения твердых тел, зависимость упругих постоянных от температуры и давления, различие между температурными зависимостями теплоемкостей Ср и Сv, и в целом, являются основным фактором, посредством которого устанавливается термодинамически равновесное распределение фононов.
Фонон-фононное взаимодействие в совокупности с дефектами кристаллической решетки ограничивает длину свободного пробега фононов, что, в свою очередь, определяет решеточную теплопроводность неметаллических кристаллов, являющуюся, фактически, теплопроводностью фононного газа.
При взаимодействии фононов с другими квазичастицами, например, с электронами зоны проводимости, фононы могут выполнять функцию “стока” для энергии, запасенной этими квазичастицами, и фактически, играют роль своеобразного внутреннего “термостата”. Именно через фононы, как правило, происходит связь квазичастиц со всеми остальными компонентами твердого тела.
Лекция 6
ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ТВЕРДЫХ ТЕЛ
Оптическое возбуждение твердых тел вызывается действием квантов электромагнитного излучения (фотонов) в диапазоне УФ, видимого и ИК-спектра. Согласно закону Эйнштейна, только поглощенный квант может оказать какое-либо воздействие на материал.
Интенсивность светового потока J (x) экспоненциально снижается в результате поглощения квантов света, в соответствии с законом Бугера – Ламберта:
J ( x ) = J ( 0 ) exp ( - x ), (6.1)
где J (0) – интенсивность падающего светового потока, - коэффициент поглощения, х – толщина поглощающего слоя.
Физический смысл коэффициента поглощения - вероятность поглощения фотона на расстоянии в единицу длины; - 1 – средняя длина свободного пробега фотона в среде – глубина проникновения света в среду (расстояние, на котором интенсивность света ослабляется в e 2.72 раз). Соответственно, размерность равна = см–1.
Поглощение
света, вызывающее возбуждение электронов
из валентной зоны в зону проводимости,
называется собственным или фундаментальным
(рис. 6.1). Естественно, для осуществления
таких переходов энергия квантов света
должна быть не ниже, чем энергия
запрещенной зоны Еg
полупроводника (![]() Еg).
Еg).
Фундаментальные оптические переходы подразделяются на прямые и непрямые (рис. 6.1) в зависимости от характера изменения волнового вектора возбуждаемого электрона.
Для
прямых переходов импульс фотона
![]() (
(![]() – волновое число фотона ) намного меньше
квазиимпульса электрона (
– волновое число фотона ) намного меньше
квазиимпульса электрона (![]() =
=
![]() ),
поскольку длина волны фотона 10-2
–
10-5
см (в диапазоне от “вакуумного“ УФ до
дальнего ИК излучения) существенно
ниже, чем типичная длина волны электрона
в кристалле (
),
поскольку длина волны фотона 10-2
–
10-5
см (в диапазоне от “вакуумного“ УФ до
дальнего ИК излучения) существенно
ниже, чем типичная длина волны электрона
в кристалле (![]() ~
~
![]() см). Поэтому импульсом фотона можно
пренебречь и записать закон сохранения
квазиимпульса электрона в виде:
см). Поэтому импульсом фотона можно
пренебречь и записать закон сохранения
квазиимпульса электрона в виде:
![]() =
или
=
или
![]() =
(правило отбора для прямых электронных
переходов), где
=
(правило отбора для прямых электронных
переходов), где
![]() и
и
![]() квазиимпульс и волновой вектор электрона
в возбужденном состоянии (в зоне
проводимости).
квазиимпульс и волновой вектор электрона
в возбужденном состоянии (в зоне
проводимости).
В случае непрямых оптических переходов закон сохранения квазиимпульса обеспечивается взаимодействием с фононами. Эти переходы осуществляются либо с испусканием либо с поглощением фонона.

Рис. 6.1. Фундаментальное поглощение в полупроводнике: а – прямые и
б – непрямые оптические переходы
При поглощении квантов света возможно такое возбуждение электронов валентной зоны, когда они не переходят в зону проводимости, а образуют квазичастицу – экситон – мигрирующее в кристалле электронное возбуждение, не связанное с переносом электрического заряда и массы.
В зависимости от эффективного расстояния между электроном и дыркой экситоны подразделяют на Френкелевские и на экситоны Ванье-Мотта. Экситон Френкеля – это, по-существу, результат возбуждения отдельного атома или молекулы в кристалле, причем такого рода внутриатомное (внутримолекулярное возбуждение) способно перемещаться по кристаллу. Такие экситоны могут существовать в кристаллах, у которых внутримолекулярное взаимодействие существенно преобладает над межмолекулярными, например, в некоторых органических полупроводниках (антрацен).
Экситоны Ванье-Мотта (большого радиуса) можно рассматривать как водородоподобное связанное состояние электрона и дырки.
Энергия кулоновского взаимодействия (Uexc) электрона и дырки в экситоне значительно ослаблена средой:
Uexp = e2 / 0 r, (6.2)
где r – эффективное расстояние между электроном и дыркой. В связи с этим величина r в сотни раз может превышать период решетки кристалла, а энергия связи в экситоне Ванье-Мотта обычно в 100 – 1000 раз меньше, чем энергия связи в атоме водорода.
На спектрах оптического поглощения экситонное поглощение проявляется при энергиях несколько меньших Еg, причем экситонные пики видны лучше при низких температурах. Следует подчеркнуть, что экситон, перемещаясь по кристаллу, хотя и переносит энергию возбуждения, но не переносит заряда, так как он электрически нейтральный. Спин экситона равен либо нулю, когда спины электрона и дырки, входящих в экситон, антипараллельны (синглетные экситоны), либо единице (триплетные экситоны).
Экситоны характеризуются ограниченным временем жизни (обычно 10-4 – 10-7 с), причем триплетные экситоны обычно более долгоживущие, чем синглетные. Гибель экситона связана с рекомбинацией входящих в него электрона и дырки (излучательной либо безызлучательной), а также с вовлечением электронов и дырок в квазихимические реакции, процессы с переносом зарядов и др.
Лекция 7
ДЕФЕКТЫ В ТВЕРДЫХ ТЕЛАХ
Любые отклонения от периодической структуры кристалла (нарушения правильного расположения атомов или ионов в узлах кристаллической решетки) можно рассматривать как появление дефектов.
В зависимости от их геометрии дефекты подразделяются на точечные (нульмерные), линейные (одномерные), поверхностные (двумерные) и объемные (трехмерные).
Типичными представителями точечных дефектов являются вакансии, междоузельные атомы, примесные атомы внедрения и замещения ( в разбавленных твердых телах ), центры окраски.
Вакансия – простейший дефект (обозначается “”) – узел решетки, в котором отсутствует атом или ион. В ионных кристаллах дефекты Шоттки обычно образуются в виде пары из двух вакансий противоположного заряда ввиду необходимости соблюдения требования электронейтральности.
В щелочногалоидных кристаллах образованием вакансий довольно просто управлять, в частности, введением двухзарядных ионов. Например, если в процессе выращивания кристалла KCl ввести CaCl2, то ион Ca+2, располагаясь в узле решетки заместит один катион (K+), на два аниона Cl-. В итоге образуется одна катионная вакансия.
Один из путей образования вакансий в простых веществах – испарение атомов с поверхности с последующим переходом на их места атомов из низлежащих слоев. Этот процесс можно рассматривать как движение вакансий от поверхности вглубь кристалла. В итоге формируются структуры разрыхления.
В простейшем случае в состоянии теплового равновесия вероятность образования вакансий (Р) определяется энергией Е , необходимой для перемещения атома из узла решетки внутри кристалла в узел на поверхности:
![]() .
(7.1)
.
(7.1)
Тогда
равновесная концентрация вакансий
![]() приближенно (при условии
<<
N)
равна:
приближенно (при условии
<<
N)
равна:
![]() .
(7.2)
.
(7.2)
Оценка
по этому уравнению в случае Е
~
1 эВ, Т ~ 1000 К дает значение
![]() ~ 10-5,
то есть ориентировочно около 1017
вакансий на 1 см3
кристалла.
~ 10-5,
то есть ориентировочно около 1017
вакансий на 1 см3
кристалла.
Наряду
с дефектами Шоттки к важнейшим точечным
дефектам относятся дефекты Френкеля,
представляющие собой комбинацию
межузельного атома и вакансии. Как и
дефекты Шоттки, эти дефекты возникают
при нагревании, а также при облучении
потоком ядерных частиц (например, потоком
быстрых электронов). Равновесная
концентрация СFr
дефектов Френкеля определяется
температурой, исходной концентрацией
узлов (Сi)
и междоузельных положений (![]() ),
а также характерными частотами колебаний
атомов решетки при наличии этих дефектов
()
и при их отсутствии (
),
а также характерными частотами колебаний
атомов решетки при наличии этих дефектов
()
и при их отсутствии (![]() ):
):
![]() .
(7.3)
.
(7.3)
В этом уравнении энергия активации ЕFr необходима для смещения атома из узла в междоузлие.
Точечные дефекты, поглощающие видимый свет в спектральном диапазоне, в котором отсутствует собственное поглощение кристалла, называют центрами окраски.
Первыми обнаруженными центрами окраски были F-центры, представляющие собой анионные вакансии, захватившие электрон. Затем были обнаружены и другие виды центров окраски: F- или F - анионная вакансия, захватившая два электрона; F2 (или М-центр) – электрон, захваченный двойной анионной вакансией; R-центр – три соседних F-центра в щелочногалоидных кристаллах и др.
Наряду с электронными, известны дырочные центры окраски, например, Vk – “ автолокализованная “ дырка в ионном кристалле, а также центры, связанные с внедрением водорода ( U-центры ), частиц коллоидного металла ( X-центры ) и др.
Как правило, центры окраски образуются в результате действия актиничного (с энергией квантов, превышающей ширину запрещенной зоны кристалла) электромагнитного (УФ-, рентгеновское, ) либо ионизирующего ( -, , нейтроны) излучения. Типичный пример образования F-центра в кристалле NaCl включает генерацию электронно-дырочной пары при действии -излучения в вакууме, захват дырки анионом Cl- с образованием атомарного Cl, уход которого из решетки вызывает образование анионной вакансии, и последующим захватом электрона этой вакансией.
Достаточно легко образуются F-центры в ZnO, MgO, TiO2, WO3 при УФ облучении в условиях вакуума. При нагревании, а иногда и при действии кислорода воздуха при комнатной температуре, они могут разрушаться, и кристалл обесцвечивается. В некоторых случаях, процессы фотоиндуцированного окрашивания и обесцвечивания являются хорошо обратимыми, что составляет основу использования так называемых фотохромных материалов, обратимо темнеющих при действии света.
Лекция 8
Диффузионные процессы в твердых телах
Диффузия – неравновесный процесс – частный случай явлений массопереноса, вызываемый тепловым молекулярным движением и приводящий к установлению равновесного распределения концентраций внутри фаз. Диффузия – процесс необратимый, приводящий к выравниванию химических потенциалов компонентов системы.
Механизмы диффузии в твердотельных системах подразделяют на:
а) вакансионный (обмен местами атомов кристалла с вакансиями);
б) междоузельный (перемещение атомов по междоузлиям);
в) бездефектные (одновременное циклическое перемещение нескольких атомов либо обмен местами двух соседних атомов).
Важнейшими законами диффузии являются:
I закон Фика:
j = - D c, (8.1)
где j – диффузионный поток, D – коэффициент диффузии, c – градиент концентрации; знак “минус” означает, что поток направлен в сторону уменьшения концентрации.
II закон Фика:
 ,
(8.2)
,
(8.2)
в случае независимости D от концентрации с принимающий вид:
 .
(8.3)
.
(8.3)
Коэффициент диффузии D зависит от температуры Т и от энергии активации диффузии Еа в соответствии с уравнением Аррениуса:
D = D0 exp ( - Ea / kT ). (8.4)
В простейшем случае, когда коэффициент диффузии не зависит от концентрации диффундирующего компонента, энергию активации Еа можно найти из наклона зависимости lg D, 1/T по уравнению:
 (
эВ), (8.5)
(
эВ), (8.5)
полученному логарифмированием соотношения (8.4).
В рамках вакансионного механизма диффузии предполагается, что для перехода атома из узла в вакансию, ему нужно преодолеть потенциальный барьер. При этом, чтобы минимизировать вероятность обратного процесса (возвращения атома на свое прежнее место) атом должен отдать часть энергии Е за счет сильного взаимодействия с соседями. Соответственно, время нахождения данного атома в узле, соседнем с вакансией
= 0 exp ( E / kT ), (8.6)
где 0 10-13 с (время порядка периода колебаний атомов в решетке), а коэффициент самодиффузии равен:
 ,
(8.7)
,
(8.7)
где U – энергия образования вакансии, – постоянная решетки.
Лекция 9
ФАЗОВЫЕ ПЕРЕХОДЫ
Переход вещества из одной фазы в другую – фазовый переход – связан с качественными изменениями свойств: характера движения структурных элементов (атомов, ионов, молекул), степени и характера упорядоченности структуры вещества, а также таких свойств, как плотность, модуль упругости, температура плавления, электрические и магнитные свойства.
Поскольку
в условиях термодинамического равновесия
химические потенциалы каждого компонента
в различных фазах системы одинаковы, в
веществе, состоящем из
компонентов, может одновременно
сосуществовать не более
![]() равновесных фаз (правило фаз Гиббса).
Однако в твердых телах, существование
выраженных диффузионных ограничений
может обуславливать возникновение
неравновесных фаз, которые могут
сосуществовать с фазами равновесными
(соответственно, возникают отклонения
от правила фаз).
равновесных фаз (правило фаз Гиббса).
Однако в твердых телах, существование
выраженных диффузионных ограничений
может обуславливать возникновение
неравновесных фаз, которые могут
сосуществовать с фазами равновесными
(соответственно, возникают отклонения
от правила фаз).
Фазовые переходы по сути являются кооперативными, связанными с согласованным взаимодействием большого числа частиц.
В химии твердого тела фазовые превращения можно разделить на два основных типа: реконструктивные и деформационные. Реконструктивные связаны с коренной реорганизацией структуры – разрывом большого количества исходных химических связей с образованием новых. Типичный пример – фазовый переход “графит - алмаз”, в котором из слоистой гексагональной структуры sp2-гибридизованного углерода формируется трехмерная решетка sp3-гибридизованного углерода.
Деформационные фазовые переходы обусловлены, преимущественно, искажениями химических связей и несущественными трансформациями кристаллической структуры. При этом симметрия решетки низкотемпературной модификации обычно характеризуется подгруппой той же пространственной группы, что и у решетки высокотемпературной модификации, но, как правило, с более низким типом симметрии. В свою очередь, как реконструктивные, так и деформационные фазовые превращения можно классифицировать по степени вовлечения в них первой либо второй координационной сферы (классификация Бюргера).
Очевидно, что реконструктивные фазовые переходы, затрагивающие первую координационную сферу (например, алмаз ↔ графит) протекают с очень большой энергией активации и характеризуются существенными кинетическими затруднениями.
Часто именно эти кинетические затруднения блокируют такого рода переход: например, хотя при нормальных условиях термодинамически стабильной полимерной модификацией углерода является графит, а алмаз – метастабильная форма углерода, при 25С и давлении 1 атм переход алмаза в графит, очевидно, не происходит из-за очень большой энергии активации.
Фазовые переходы в твердых телах


затрагивающие I
координационную сферу
затрагивающие II
координационную сферу
с изменением характера
хим. связи (медленные) -
Sn↔-
Sn
“порядок - беспорядок”
Реконструктивные (медленные)
Алмаз –
графит
Реконструк- тивные (медленные)


Переходы замещения (медленные)
Деформацион- ные (быстрые)
Ориентационные и вращательные (быстрые) Сегнето- параэлектрик NH4H2PO4
Деформационные (быстрые) Структура
NaCl/CsCl
Иными словами, алмаз является термодинамически нестабильной, но кинетически устойчивой модификацией углерода. Любопытно, однако, что в ультрадисперсном (нанокристаллическом) состоянии, согласно новым представлениям, алмаз может проявлять большую устойчивость, чем графит.
В настоящее время принятой является более широкая трактовка понятия фазовых переходов типа “порядок - беспорядок”. Считается, что эти переходы, называемые еще и структурными фазовыми переходами, полиморфными превращениями, в твердых телах обусловлены перестройкой структуры твердых тел в результате изменения взаимного пространственного расположения атомов, ионов либо их групп таким образом, что происходит изменение типа симметрии кристалла.
Структурные фазовые переходы подразделяются на собственные, сопровождающиеся изменением точечной симметрии кристалла и несобственные – когда изменяется трансляционная симметрия. Несобственные переходы приводят к возникновению сверхструктур и доменов.
Изменение структуры твердого тела, связанное с фазовым переходом, естественно, вызывает изменение энтропии в точке фазового перехода. Это изменение состоит из конфигурационного, колебательного, вращательного и электронного вкладов, причем, как правило, конфигурационный вклад оказывается преобладающим. Например, -AgI, имеющий гексагональную элементарную ячейку с двумя ионами Ag+ в тетраэдрической позиции может переходить при 145С в объемноцентрированную кубическую структуру (-AgI), в которой ионы Ag+ распределены по 12 тетраэдрическим позициям. Происходящее при этом изменение конфигурационного вклада энтропии равно:
 ,
(9.1)
,
(9.1)
где
- число Авогадро,
![]() - газовая постоянная,
- постоянная Больцмана,
- газовая постоянная,
- постоянная Больцмана,
![]() (числа конфигураций, то есть возможных
позиций ионов Ag+).
Рассчитанное по этому уравнению значение
(числа конфигураций, то есть возможных
позиций ионов Ag+).
Рассчитанное по этому уравнению значение
![]() Дж
моль-1
К-1
действительно хорошо согласуется с
экспериментальными данными.
Дж
моль-1
К-1
действительно хорошо согласуется с
экспериментальными данными.
Одним из специфических типов структурных фазовых переходов рода являются так называемые мартенситные превращения. В ходе этих превращений перестройка кристаллической решетки связана обычно, с относительно небольшой деформацией ее элементарной ячейки. Поскольку относительные смещения атомов (молекул) малы по сравнению с межатомным расстоянием (0.01 – 0.001), энергетический барьер этого процесса мал по сравнению с энергией связи частиц в кристалле. Поэтому скорость мартенситного превращения очень велика, причем этому способствует именно отсутствие в данном процессе диффузионно-лимитированных стадий.
Типичным примером мартенситного превращения является переход аустенита (гранецентрированного кубического твердого раствора углерода в -Fe) в мартенсит – метастабильную тетрагональную фазу, возникающую, в частности, в процессе закалки стали. Кроме того, мартенситные превращения были обнаружены для ряда других кристаллических материалов: Ti, U, Na, Zr, Ce, Tl; сплавах типа Cu-Zn-Al и др., ионных и ковалентных кристаллах типа ZrO2 и др.
Мартенситные превращения обычно протекают по сдвиговому механизму и внутри кристалла исходного аустенита формируются пластины мартенсита. Эти пластины, как правило, не являются монокристаллическими, а представляют собой пакеты плоскопараллельных доменов. Деформация материала, содержащего такого рода домены, происходит преимущественно за счет смещения доменных границ (“сверхупругость”). В целом, формирование мартенситных кристаллов и трансформация их стремлением системы к минимуму упругой энергии.
При нагревании имеет место обратное превращение мартенсита в исходную (аустенитную) фазу, причем в некоторых случаях с полным восстановлением первоначальной формы материала (так называемая “память формы”), но чаще – с ее частичным восстановлением. Во многих случаях мартенситные превращения осложнены процессами рождения и перемещения дислокаций, вызывающими пластические релаксации внутренних напряжений и, соответственно, необратимость этих превращений (появляется гистерезис – разность температур начала мартенситного и обратного превращений в несколько сотен градусов для системы “мартенсит - аустенит”, около 200С для перехода моноклинной модификации ZrO2 в тетрагональную, и всего несколько градусов для сплава Cu-Zn-Al).
Мартенситные (“бездиффузионные”) превращения, в совокупности с диффузионным перераспределением компонентов и изменением атомного порядка, лежат в основе методов целенаправленного изменения структурных свойств, прочностных характеристик и других практически важных свойств многих металлов и сплавов с помощью их термической и механической обработки.
С точки зрения изменения термодинамических параметров к фазовым переходом рода относятся переходы, характеризующиеся равенством удельных энергий Гиббса (термодинамических потенциалов) обеих фаз в точке фазового перехода, при том, что первые производные энергии Гиббса по температуре и давлению претерпевают скачкообразное изменение. Учитывая, что
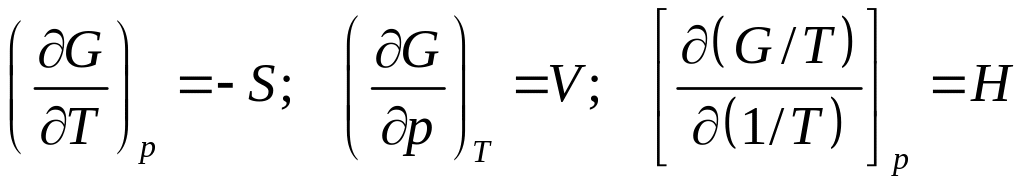 ,
(9.2)
,
(9.2)
в точке фазового перехода на температурной зависимости энтропии, удельного объема, а также энтальпии имеется разрыв.
К фазовым переходам рода относятся переходы, сопровождающиеся скачком вторых производных энергии Гиббса по функциям состояния в точке превращения:
 (9.3)
(9.3)
где
![]() - теплоемкость,
- теплоемкость,
![]() - коэффициент термического расширения,
- коэффициент термического расширения,
![]() - коэффициент сжимаемости.
- коэффициент сжимаемости.
Лекция 10
КИНЕТИКА ТВЕРДОФАЗНЫХ РЕАКЦИЙ
Твердофазные гетерогенные взаимодействия, как правило, представляют собой многостадийные процессы, включающие доставку реагирующих компонентов в зону реакции, собственно химическое взаимодействие, отвод продуктов реакции, происходящий обычно по диффузионному механизму. Результирующая скорость поцесса определяется скоростью самой медленной стадии, и если это диффузия, то говорят, что процесс лимитируется диффузией и кинетика процесса - диффузионная. Если наиболее медленной стадией является химическая реакция, процесс лежит в кинетической области и кинетика, соответственно, - химическая. В некоторых случаях лимитирующей стадией оказывается стадия образования новой фазы – зародышеобразование.
Типичным примером твердофазных реакций являются процессы термического разложения твердых тел (термолиз). Поскольку фононы имеют существенно меньшую энергию, чем фотоны, используемые в процессах фотолиза, термолиз оказывается более локализованным на дефектных местах кристалла, чем фотолиз, и тем более, чем радиолиз. В случае термолиза генерация электронно-дырочных пар не играет той роли, которую она играет при фотолизе. Более того, если в химическом соединении анион или катион является сложным, то возбуждение может сосредоточиться внутри соответствующей анионной либо катионной подрешетки:
2MnO4- → MnO42- + MnO4o (10.1)
|→ MnO2 + O2 .
В ряде случаев оказываются более выгодными не электронные переходы, а протонные:
NH4ClO4 → NH3 + HClO4. (10.2)
В целом, процессы термолиза преимущественно обусловлены локальными переходами электронов из валентной зоны на примесные уровни с последующим химическим актом. Таким образом, три элементарных стадии – возбуждение, миграция и локализация при термолизе объединены в один. Эти обстоятельства резко повышают роль дефектной подсистемы.
Как процессы термолиза, так и многие другие твердофазные реакции характеризуются рядом общих особенностей, и в первую очередь тем, что определяющее значение играет пространственное расположение реагирующих молекул, процессы массопереноса, состояние дефектной подсистемы, предыстория образца. В совокупности эти особенности позволили объединить такого рода процессы под общим названием «топохимические» процессы. Термин «топохимия» предполагает, что реакция контролируется структурой кристаллической решетки, может идти в каждой точке объема кристалла и при этом вступающие в реакцию молекулы испытывают минимальные атомные или молекулярные перемещения (по крайней мере на начальных этапах процесса).
На начальной стадии твердофазного взаимодействия важное значение имеет процесс образования зародышей новой фазы. Во многих случаях на этой стадии имеет место автокаталитический рост скорости, затем размер зародышей продолжает возрастать и они начинают соприкасаться, и, постепенно скорость процесса снижается. Типичная зависимость степени превращения и скорости превращения (dα/dt) от времени (рис. 10.1) характеризуется так называемой s-образной (или «сигмоидной») кривой, изображенной на рис. 10.1.

Рис. 10.1. Зависимости степени превращения от времени (а) и скорости превращения от степени превращения (б)
Для оценки скорости твердофазного взаимодействия обычно используется величину, называемую степенью превращения:
α = (xo-x) / xo, (10.3)
где хo - начальное количество вещества, x - количество вещества в момент времени τ.
Как упоминалось выше, важнейшей составляющей твердофазных процессов является процесс диффузии. В простейшем случае роль диффузии можно проиллюстрировать хорошо известными экспериментами, в которых исследовалось взаимодействие пластинок из серебра, меди и свинца со свободными галогенами в изотермических условиях. Было установлено, что скорость роста слоя галогенида металла описывается уравнением:
dx/dt = kx-1, (10.4)
где x – толщина слоя продукта, t - время, k - константа, зависящая от природы металла и галогена, а также от условий реакции, причем впоследствии было показано, что k = krD, где kr – константа, D - коэффициент диффузии. Объединяя это выражение с уравнением (10.4), интегрируя с учетом граничных условий x = 0 при t = 0, находим:
x2 = 2krDt = kpt, либо x = (kp)1/2t1/2 , (10.5)
где kp - константа скорости параболического роста продуктов.
С учетом этой простейшей зависимости скорости процесса от времени в диффузионно-контролируемых условиях Яндером была предложена модель для описания кинетики реакций в порошкообразных системах. Принималось, что порошкообразный компонент A состоит из одинаковых по размеру сферических частиц с начальным радиусом Ro. Компонент B быстро образует непрерывный слой продукта C на поверхности частиц A по реакции
Aтв + Bтв = Cтв + Dг, (10.6)
причем реакция лимитирована объемной диффузией компонента B через слой продукта к компоненту A, а коэффициент диффузии не зависит от времени. Примером такой реакции может быть взаимодействие диоксида кремния с карбонатом бария:
SiO2 + BaCO3 = BaSiO3 + CO2 . (10.7)
Исходя из геометрических аспектов данной задачи, для сферических частиц можно записать:
 .
(10.8)
.
(10.8)
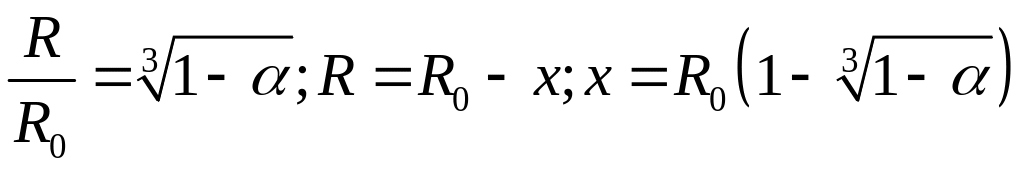 .
(10.9)
.
(10.9)
Объединяя выражения (10.9) и (10.5), получаем известное уравнение Яндера:
 ,
(10.10)
,
(10.10)
иллюстрирующее временную зависимость степени превращения в ходе протекания твердофазной реакции, лимитированной диффузией.
Общая характеристика различных
типов материалов
Введение
Третий раздел программы курса предполагает изучение основных физических и химических свойств твердотельных материалов различных типов, которые находят применение во многих отраслях промышленности, существующих и развивающихся в Республике Беларусь, или представляют научный и практический интерес для современной науки и техники. Изучаемые материалы разделены на три основных типа твердых тел, причем в основу разделения положены особенности химической связи в веществах, а также величина и механизм проводимости. Соответственно в лекционном курсе рассматриваются наиболее распространенные металлические, полупроводниковые и диэлектрические материалы, их физические свойства, обусловливающие практическое применение, особенности химической связи и кристаллической (либо некристаллической) структуры, а также влияние различных факторов на свойства твердотельных материалов, среди которых доминирует влияние природы, концентрации и распределения примесей и дефектов, строение твердых тел (порошки, монокристаллы, пленки, скелетные и пористые структуры, наночастицы) и состояние их поверхности. Особое внимание уделяется различным аспектам применения твердотельных материалов и возможностям прогнозирования практически значимых свойств твердых тел в зависимости от их состава и строения.
Лекция 11 Полупроводниковые материалы: Физические свойства, Особенности химической связи
Цель лекции – ознакомление с особенностями физических свойств, кристаллической структуры и химической связи в полупроводниковых материалах различного химического состава.
Особенности электрофизических свойств полупроводниковых материалов. Первое и одно из основных отличий полупроводников от металлов и диэлектриков, которое не является единственным, состоит в их зонном строении и характере заполнения зон электронами, а отсюда – в величине проводимости. Металлы обладают высокой электропроводностью ( = 104 ÷ 106 Ом-1см-1), диэлектрики имеют ≤ 10-10 Ом-1см-1), полупроводники занимают промежуточное положение ( = 10-9 ÷ 103 Ом-1см-1), хотя приведенные граничные значения проводимости довольно условны.
Второе отличие состоит в том, что проводимость полупроводников и диэлектриков быстро возрастает с ростом температуры, в то время как электропроводность металлов при повышении температуры довольно ощутимо уменьшается (рис. 11.1). Объяснить этот факт можно, понимая различие в температурной зависимости электропроводности у металлов, с одной стороны, и у полупроводников и диэлектриков, с другой стороны. Величина электропроводности определяется концентрацией носителей заряда (n, см-3), подвижностью этих носителей (μ, см2/В∙с) и величиной заряда (е):
= neμ. (11.1)
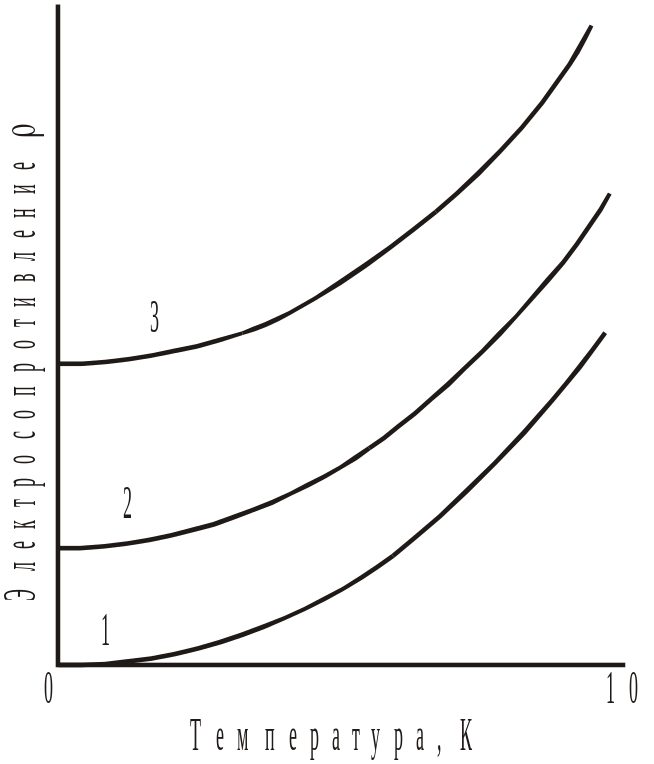

а б
Рис.11.1. Зависимость электросопротивления () металлов (а) и
электропроводности полупроводников (б) от температуры
Для всех электронных проводников, в отличие от ионных, величина заряда (е) постоянна. Величина подвижности (μ) слабо уменьшается с ростом температуры из-за увеличения интенсивности столкновений между движущимися носителями заряда и фононами, т. е. из-за рассеяния электронов вследствие колебаний узлов кристаллической решетки. Концентрация носителей заряда (n) в металлах не зависит от температуры, в то время как в полупроводниках и диэлектриках n обычно экспоненциально растет с повышением температуры. При высоких температурах проводимость отдельных диэлектриков может достигать величины, характерной для полупроводников, и, наоборот, при низких температурах некоторые полупроводники становятся диэлектриками.
Третье отличие полупроводников и диэлектриков,от металлов состоит в малой концентрации носителей. В металлах n сопоставимо с числом узлов кристаллической решетки (1022 ÷ 1023 см-3), а в полупроводниках – на много порядков меньше.
Четвертой особенностью являются необычные свойства контактов полупроводников с металлами либо двух разных полупроводников друг с другом. Зависимость возникающего напряжения от тока не линейна и не подчиняется закону Ома. Поэтому такие контакты называют неомическими. Это происходит потому, что в узкой приповерхностной зоне вблизи контакта изменяется концентрация или даже доминирующий тип носителей тока. Так, при контакте двух твердых тел (металл – металл, металл – полупроводник, полупроводник – полупроводник) электроны переходят из вещества с большей энергией уровня Ферми в вещество с меньшей энергией уровня Ферми до тех пор, пока не будет достигнута такая величина электрического поля (пространственного заряда), которая будет препятствовать дальнейшему переходу электронов. На рис.11.2 представлена зонная диаграмма выпрямляющего контакта металла с полупроводником. На диаграмме показано, что в состоянии равновесия уровень Ферми в контактирующих твердых телах выравнивается вследствие появления контактной разности потенциалов (напомним, что уровень Ферми – это наивысший заполненный при 0 К энергетический уровень в твердом теле).

а б
Рис. 11.2. Схема, иллюстрирующая образование на границе контакта металл полупроводник области пространственного заряда (помечена наличием зарядов в приповерхностном слое металла и полупроводника) EF – уровень Ферми, ESC – падение потенциала в области пространственного заряда:
а контакт с полупроводником p-типа, б контакт с полупроводником n-типа.
Если знак контактной разности потенциалов таков, что концентрация носителей становится меньшей, чем в объеме полупроводника, то приконтактный слой определяет электросопротивление всей системы. Приложенное внешнее электрическое поле в зависимости от знака разности потенциалов либо дополнительно уменьшает концентрацию носителей в приконтактной области, либо увеличивает их концентрацию. Таким образом, сопротивление контакта для токов в прямом и обратном направлениях существенно различается, что и обеспечивает выпрямляющие свойства контакта.
Протяженность области пространственного заряда в полупроводниках существенно больше, чем в металлах (10-6÷10-7м и 10-9÷10-10 м, соответственно), а концентрация зарядов, наоборот, меньше. Такие особенности позволяют широко использовать контактные явления на практике. Так, работа большинства полупроводниковых приборов (например, диодов, транзисторов) основана на использовании контактных явлений на границе между электронным и дырочным полупроводником
Пятое отличие состоит в величине термоэлектродвижущей силы (ЭДС), которая возникает в месте контакта двух твердых тел и зависит от их природы и температуры. Подобные явления подразделяются на ряд разновидностей, составляющих группу термоэлектрических явлений (эффекты Томсона, Пельте, Зеебека), на которых основана работа термопар, используемых для измерения температуры, термоэлектрических холодильных установок и термоэлектрических источников энергии.
Так, эффект Томсона обязан своему происхождению тем, что подвижность и кинетическая энергия носителей заряда возрастают с увеличением температуры. Поэтому при установившемся температурном режиме тепловая энергия электрона на горячем конце стержня больше, чем на холодном. Таким образом, от горячего конца к холодному переходит большее количество носителей заряда, чем в обратном направлении. В итоге между холодным и горячим концом стержня возникает разность потенциалов. Результирующая ЭДС задается соотношением
Е = ΔТ, (11.2)
в котором коэффициент пропорциональности называется коэффициентом Томсона, а Е составляет несколько милливольт.
Выделяющееся количество теплоты Q пропорционально силе тока I, времени t, разности температур ΔТ и равно
Q = ΔТ I t. (11.3)
В случае полупроводников знак термо ЭДС зависит от типа проводимости (р - или n - тип).
Эффект Пельтье состоит в том, что при пропускании электрического тока в определенном направлении на границе двух разнородных проводников (или полупроводника и металла) выделяется или поглощается теплота. Зонная структура контакта металл – полупроводник n-типа, характерная для приповерхностных областей обоих твердых тел после установления равновесия и, соответственно, создания области пространственного заряда, приведена на рис.11.3. В полупроводнике n-типа уровень Ферми расположен на глубине U ниже дна зоны проводимости. Поэтому для перемещения электронов в электрическом поле через контакт слева направо необходима энергия U для перехода из валентной зоны металла в зону проводимости полупроводника и еще дополнительно энергия, равная 3/2kT, соответствующая кинетической энергии свободных электронов. По этой причине прохождение электронов через место контакта приводит к его охлаждению, что используется, например, в термоэлектрических холодильных установках. При прохождении электрического тока в обратном направлении, справа налево, место контакта, наоборот, разогревается. Количество поглощаемой или выделяющейся теплоты определяется соотношением
Q = ПI t = I/е0(U + 3/2 kT), (11.4)
где П – коэффициент Пельтье.

Рис.11.3. Зонная структура на границе контакта металл – полупроводник, объясняющая возникновение эффекта Пельтье
Эффект Зеебека проявляется, когда ЭДС возникает в замкнутом контуре, образованном двумя разнородными проводниками, причем оба их контакта находятся при разной температуре. Поскольку градиенты температуры устанавливаются в обоих проводниках, в них возникает ЭДС Томсона. Помимо этого, на каждом из контактов двух разнородных тел возникает ЭДС Пельтье. Результирующая по всему контуру ЭДС равна алгебраической сумме двух ЭДС Томсона и двух ЭДС Пельтье. Коэффициенты Пельтье и Зеебека (α) связаны между собой соотношением
П = αТ, (11.5)
где Т – абсолютная температура.
Эффект Зеебека лежит в основе действия термопар, способных с высокой точностью измерять температуру, и что особенно важно – в области высоких температур, ограничиваемых лишь температурой плавления материалов, составляющих контур. Набор из n последовательно соединенных термопар образует термобатарею, ЭДС которой в n раз больше, чем у одной термопары. Такие термобатареи используются для преобразования солнечной энергии, в космических исследованиях. Материалы с большими коэффициентами Пельтье и Зеебека применяются в термоэлектрических источниках энергии и системах охлаждения. Поскольку полупроводники характеризуются гораздо большими значениями коэффициентов, чем металлы, казалось бы, их применение особенно эффективно. Однако следует отметить, что из-за низкой электропроводности большие потери энергии происходят вследствие выделения джоулевского тепла. По этой причине оптимальным является использование полупроводниковых материалов с малой теплопроводностью (например, Bi2Te3, Bi2Se3, PbTe). Полупроводниковую термопару изготавливают на основе халькогенида, причем одна ветвь имеет n-тип, а другая p-тип проводимости.
Шестое отличие полупроводников от металлов состоит в природе носителей заряда. В металлах носителями заряда являются только электроны, в то время как в полупроводниках – электроны, дырки, иногда – катионы или анионы (ионная проводимость).

Рис.11.4. Возникновение эффекта Холла в полупроводнике
Получить информацию о природе проводимости (если она электронная или дырочная) можно с помощью эффекта Холла. Этот эффект относится к гальваномагнитным явлениям и заключается в том, что если образец, через который протекает ток, поместить в магнитное поле напряженностью Н, но в направлении, перпендикулярном электрическому полю и току, возникает электрическое холловское поле и появляется электродвижущая сила (рис. 11.4). При не сильных магнитных полях холловское напряжение (Ен) пропорционально произведению силы тока и напряженности магнитного поля
ЕН = RH IH/d, (11.6)
где d – толщина пластинки, RH – коэффициент пропорциональности, называемый постоянной Холла, причем:
RH = 1/ne (см3/к). (11.7)
Перемножив уравнения (11.1) и (11.7) получим
RH = μ. (11.8)
Таким образом, экспериментально (и независимо) определяя удельную проводимость и постоянную Холла, можно вычислить подвижность носителей тока, а также их концентрацию. Большинство металлов имеет отрицательные коэффициенты Холла, а значит, носителями тока в них являются электроны. Положительное значение RH указывает на тот факт, что носителями заряда являются дырки (электронные вакансии). Последнее характерно для полупроводников с дырочным типом проводимости и некоторых металлов (например, цинк, кадмий).
Отметим, что в собственных полупроводниках число свободных электронов равно числу дырок, и при равенстве подвижности носителей заряда обоих знаков результирующая ЭДС Холла должна быть равной нулю. В действительности же электроны, как правило, более подвижны, чем дырки, в результате чего возникает результирующая RH, свидетельствующая о проводимости n-типа. В таких случаях концентрация носителей, вычисленная из коэффициента Холла, не соответствует действительности, что свидетельствует о необходимости осторожного отношения к интерпретации величины RH.
Ионные проводники обычно имеют очень низкие значения μ и n, что не дает возможности наблюдать эффект Холла, хотя в некоторых твердых электролитах с относительно большой подвижностью ионов эффект Холла может быть обнаружен (например, в RbAg4I5, где относительно высока Ag+-ионная проводимость, = 1 Ом-1 см-1 при 25 оС).
Исследования ионной проводимости состоят в определении относительной подвижности ионов. Для этого исследуемый кристалл помещают в электрическое поле между двумя металлическими электродами. При доминировании катионного тока увеличивается масса катода. Если доминирует анионный ток, возрастает масса анода.
Седьмой особенностью подавляющего большинства полупроводников в сравнении с металлами является способность к резкому изменению электрических свойств при введении ничтожно малого количества электрически активных примесей, а также чрезвычайная чувствительность к дефектам в кристаллах. Так, границей чувствительности к примесям, способным повлиять на величину сопротивления полупроводника,будет концентрация примеси 10-10 ат. %. Влияние примесей и дефектов иллюстрирует и тот факт, что кремний в зависимости от того, является он моно- или поликристаллическим, а также от уровня легирования и природы легирующей примеси, может иметь удельное сопротивление в широком диапазоне 0,005÷2000 Ом·см.
Собственная проводимость полупроводника становится заметной лишь при достаточно высокой температуре, значение которой зависит от ширины запрещенной зоны. Чем больше ΔЕ, тем выше эта температура. При комнатной температуре собственная проводимость становится ощутимой при ΔЕ ≈ 0,2 эВ, например, у антимонида индия. Практически более важной является примесная проводимость. Различают два вида примесных энергетических уровней: донорные и акцепторные. Первые располагаются в запрещенной зоне немного ниже дна зоны проводимости и именно с них электроны переходят в зону проводимости. При этом доноры превращаются в положительно заряженные ионы, которые не участвуют в электронной проводимости, а полупроводник имеет n-тип проводимости. Акцепторные уровни располагаются выше потолка валентной зоны и захватывают электроны от нее, оставляя свободные электронные состояния – дырки. Этот захват сопровождается превращением акцепторов в положительно заряженные ионы, которые также не участвуют в электропроводности. В таком случае полупроводник приобретает дырочный, или р-тип, проводимости. Энергия ионизации электрически активных примесей составляет обычно не более 0,1 эВ.
Восьмой особенностью полупроводниковых материалов является их высокая чувствительность к свету и ионизирующим излучениям. Под действием электромагнитного излучения в полупроводниках может возникать фототок, т. е. генерируются пары электрон – дырка, причем электроны и дырки обладают разной подвижностью и разным временем жизни; в результате фиксируют резко возросшую электронную (реже дырочную) проводимость. Собственное поглощение излучения (т. е. не электронами примеси, а собственными электронами валентной зоны) возможно лишь при энергии излучения не меньшей, чем ширина запрещенной зоны. Эта минимальная энергия hγ = ΔE называется порогом или краем поглощения. Это означает, что для длин волн λ > λмакс = 2π hc/ΔE чистый полупроводник прозрачен.
Такое свойство полупроводников находит применение для создания фоторезисторов, фотодатчиков, фотодиодов, приемников излучения, для записи информации.
Особенности химической связи в полупроводниковых материалах. Зонная теория твердого тела является разделом квантовой механики, в котором рассматривается движение электронов в твердом теле с периодическим расположением узлов. Следовательно, она удовлетворительно бъясняет специфические особенности кристаллических полупроводников. Однако открытие огромного разнообразия полупроводниковых соединений различной природы, в том числе аморфных и стеклообразных, органических полупроводников, жидких кристаллов, свидетельствует о том, что полупроводниковые свойства в первую очередь определяются не кристаллической структурой, а природой химической связи в соединениях или характером межатомных связей всех атомов, входящих в состав данного вещества.
Попытаемся определить особенности химической связи, характерной для веществ с полупроводниковыми свойствами. Для этого сравним характерные признаки металлической, ионной и ковалентной связи.
Основные признаки металлической связи – ее ненаправленность, ненасыщаемость, нелокализованность. Валентные электроны атомов металла, хотя и обобществлены, что характерно также для ковалентной связи, однако делокализованы по всей кристаллической решетке. Количество носителей заряда велико и сопоставимо с числом атомов, оно не может быть увеличено с повышением температуры или под воздействием света. Энергетические зоны, сформированные внешними s- и p- орбиталями, перекрываются. Значит запрещенная зона отсутствует. Рассмотренные выше электрофизические не могут реализовываться свойства для твердого тела с металлической связью.
Качественное и количественное описание ионной связи возможно без привлечения квантовой механики, поскольку доминирующим механизмом является электростатическое кулоновское взаимодействие: притяжение между разноименными ионами и отталкивание одноименных ионов. Сила этого взаимодействия (F) зависит от заряда ионов (еА и еВ) и расстояния между ними (rA + rB):
Fε = еАеВ:( rA + rB)2 (11.9),
где ε – диэлектрическая проницаемость твердого тела. Ионы одного знака окружены возможно большим числом противоионов, которые отталкиваются друг от друга, и система в целом характеризуется шаровой симметрией.
В идеальной кристаллической ионной решетке катионы и анионы имеют, как правило, устойчивую электронную оболочку инертного газа и поэтому только при сильных энергетических воздействиях способны принимать или отдавать электроны. В рамках представлений о зонной структуре ионных кристаллов указанная особенность приводит к тому, что на энергетической диаграмме имеется широкая запрещенная зона. По этим причинам чистые ионные кристаллы стехиометрического состава являются диэлектриками. Электронная проводимость в них ничтожно мала, и преобладает ионная проводимость, которая усиливается при появлении в кристаллах вакансий. Так, катионная проводимость наблюдается при введении галогенида щелочно-земельного металла в кристаллы галогенида щелочного металла вследствие возникновения катионных вакансий, которые компенсируют «лишний» положительный заряд в узлах решетки, занимаемых ионами Ме2+. В случае отклонений состава ионных кристаллов от стехиометрического наблюдается слабая электронная или дырочная проводимость, причины которой мы рассмотрим позже.
Идеально ионных соединений в природе практически не существует. К чисто ионным соединениям близки только галогениды щелочных металлов, хотя и для них степень ионности связи составляет 70 - 90 %. Кроме того, эффективные заряды на типических электроотрицательных атомах не превосходят 1е, в то время как заряды на атомах металлов могут быть больше единицы. Это объясняется тем, что энергия присоединения двух электронов к атомам отрицательна. Следовательно, оксиды, сульфиды не могут быть чисто ионными соединениями. Представления об ионной связи многих соединений сформировались исторически с учетом результатов исследований электролитической диссоциации в водной среде, а также под влиянием представлений об окислительно-восстано-вительных реакциях, согласно которым число отдаваемых или присоединяемых электронов определяется по условной степени окисления атомов. В большинстве реальных соединений связи являются ионно-ковалентными: шаровая симметрия нарушена, электронные облака деформированы, наблюдается явление поляризации. Дипольный момент (μ) определяется зарядом иона (z) и расстоянием между противоионами (Δd) или же напряженностью электрического поля, создаваемого катионом (Е), и поляризуемостью аниона (α):
μ = zΔd = Еα.. (11.10)
Чем больше заряд катиона и меньше его радиус, тем более сильное поле создает катион, оказывая поляризующее действие на анион. Последний тем более поляризован, чем сильнее электрическое поле, создаваемое катионом, и больше радиус (размытие электронных облаков) аниона.
Для веществ с полупроводниковыми свойствами характерна ковалентная связь. Эта связь в простейшем случае образуется путем обобществления электронов двух атомов и характеризуется такими признаками, как локализованность, направленность, насыщаемость. Так, при образовании ковалентных связей в кристаллической решетке кремния четыре валентных электрона (3s2, 3p2) участвуют в sp3 гибридизации и образуют электронные облака, направленные к вершинам тетраэдра таким образом, чтобы потенциальная энергия системы была минимальна. Каждая пара атомов связана парой электронов с симметричным распределением электронной плотности. У германия характер связи аналогичен, но в гибридизованном состоянии находятся 4 s и 4 p электроны, связывающие электронные облака более протяженны и имеют меньшую плотность в области перекрывания.
У химических соединений гомеополярная связь не возникает, поскольку электронная пара смещена в сторону более электроотрицательного атома. Возникает полярная или ионно-ковалентная связь. В случаях, когда электронные облака, осуществляющие ковалентную связь, деформированы и размыты, т. е. связь не особенно прочна, электроны могут возбуждаться, и уже при не особенно больших затратах энергии возможен разрыв химической связи с формированием подвижного электрона и электронной вакансии (дырки). Исходя из представлений о зонной структуре таких твердых тел, валентный электрон, повысив свою энергию на величину, равную или немного превышающую энергию ширины запрещенной зоны, попадает в зону проводимости и становится способным перемещаться по кристаллу. Важными характеристиками, позволяющими прогнозировать наличие полупроводниковых свойств в твердотельных материалах, являются степень ионности связи в соединениях и разность электроотрицательностей (pис. 11.5).
Напомним, что для CsF степень ионности связи максимальна и равна 1. Разность электроотрицательностей (Δx) по одной из наиболее распространенных шкал Полинга определяется экспериментально как разность между энергией диссоциации соединения АВ (D(A—B)) и полусуммой энергий диссоциации молекул А2 (D(A—А)) и В2 (D(В—B)):
Δx = D(A—B) – 1/2[D(A—А) + D(В—B)]. (11.11)
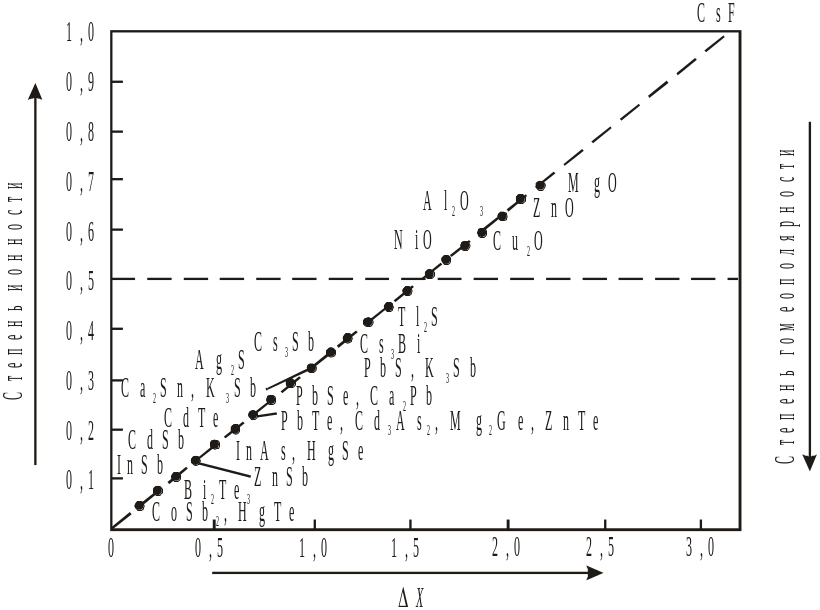
Рис. 11.5. Зависимость степени ионности от разности электроотрица-тельностей (x) в соединениях с разным типом связи
Как следует из рис.11.5, большинство полупроводниковых соединений имеют степень ионности связи менее 0,5, т. е. химическая связь в них носит преимущественно ковалентный характер.
Таким образом, вещества с полупроводниковыми свойствами это не металлы, не вещества с идеальной ионной связью и не вещества с очень прочной ковалентной связью (как, например, алмаз, у которого делокализация электронов энергетически крайне затруднена). Для полупроводниковых веществ характерны не особенно прочные ковалентные связи, ковалентные связи с определенной долей ионности или ионные поляризованные (т. е. с долей ковалентности) связи.
Количество материалов с полупроводниковыми свойствами очень велико. Одним из возможных способов их классификации является разделение на типы по признакам кристаллической структуры и химической природы. Этот способ позволяет выделить девять типов полупроводниковых материалов:
Полупроводники с алмазоподобной решеткой (кубическая гранецентрированная решетка) – кремний, германий, α-олово, антимонид индия, арсенид галлия.
Полупроводники с молекулярной решеткой: селен, теллур, органические полупроводники, например, антрацен.
Халькогениды, имеющие кристаллическую решетку типа сфалерита – сульфиды, селениды, теллуриды цинка, кадмия, ртути, свинца.
Ионные кристаллы (решетка типа NaCl): хлориды, бромиды серебра, меди (I).
Оксиды: Cu2O, NiO (тип NaCl), ZnO – (тип вюртцита).
Тройные полупроводниковые соединения: CuFeS2 – халькопирит (тип сфалерита); ZnGeAs2, SbSI.
Аморфные и стеклообразные полупроводники: Te, AsSe.
Полимеры с сопряженными связями: полиацетилен, полиакрилонитрил.
Комплексы с переносом заряда: фенилендиамин (донор π-электронов), тетрацианохинодиметан (акцептор π-электронов).
