1.2. Однофазный мостовой выпрямитель

В

Рис. 1.10. Однофазный мос­товой выпрямитель при активной нагрузке

ыпрямитель (рис. 1.10) состоит из понижающего трансформатора , имеющего одну первичную и одну вторичную обмотки. Вентили выпрямителя образуют мостовую схему выпрямления, в одну диагональ которой включено сопротивление нагрузки , другая диагональ моста соединена с вторичной обмоткой трансформатора с напряжением . Поскольку для работы выпрямителя не требуется трансформатор с нулевым выводом, выпрямительный мост может подключаться непосредственно к сети, что является преимуществом такого типа выпрямителя.

Принцип действия выпрямителя рассмотрим на примере чисто активной нагрузки . Диаграммы работы выпрямителя показаны на рис. 1.11.

Вентили выпрямителя работают попарно-поочередно. Первому полупериоду 0 –  соответствует полярность напряжения , показанная на рис. 1.10 без скобок. Это напряжение является прямым для вентилей и , через которые образуется контур протекания тока нагрузки по цепи:

. (1.49)

Напряжение подключается к нагрузке с полярностью, указанной на рис. 1.10. При нулевом падении напряжения на открытых вентилях напряжение на нагрузке повторяет форму напряжения вторичной обмотки трансформатора. Во втором полупериоде работы выпрямителя (полярность указана на рис. 1.10 в скобках) напряжение меняет знак на противоположный, и ток нагрузки замыкается через открытые вентили по контуру:

. (1.50)

Во втором полупериоде напряжение подключается к нагрузке с той полярностью, что и на интервале 0– , поэтому на рис. 1.11, в оно показано в виде однополярных положительных полуволн напряжения , повторяющих форму напряжения вторичной обмотки трансформатора. Поскольку кривые выпрямленного напряжения для мостового выпрямителя и выпрямителя с нулевым выводом идентичны по величине и по форме, то для мостового выпрямителя действительно полученное ранее соотношение: , где – действующее значение напряжения вторичной обмотки трансформатора. Для вычисления также справедливо выражение

. (1.51)

Рис. 1.11. Диаграммы работы мостового выпрямителя при активной нагрузке

При чисто активной нагрузке форма выпрямленного тока (рис. 1.11, г) повторяет форму напряжения на нагрузке (рис. 1.11, в). Среднее значение тока нагрузки зависит от величины напряжения и сопротивления нагрузки :

.

Ток нагрузки замыкается через вентили в первом полупериоде, а через – во втором, поэтому на интервале проводимости вентилей его ток повторяет форму тока нагрузки . Поскольку вентили выпрямителя работают поочередно, среднее значение тока одного вентиля вдвое меньше тока нагрузки , т. е.:

.

Определим величину обратного напряжения, которое прикладывается к закрытым вентилям выпрямителя. При работе выпрямителя под обратным напряжением находятся одновременно два вентиля на интервале проводимости двух других вентилей. В первом полупериоде 0 – (полярность напряжения показана без скобок) в проводящем состоянии находятся вентили  , к вентилям прикладывается обратное напряжение. Выясним на этом интервале величину напряжения на одном из закрытых вентилей, например . Отрицательное напряжение поступает на анод непосредственно с обмотки трансформатора (рис. 1.10), а положительное напряжение через открытый вентиль прикладывается к катоду . Таким образом, вентиль находится под обратным напряжением, определяемым напряжением обмотки трансформатора , а амплитудное значение обратного напряжения вентиля определяется соответственно амплитудным значением напряжения :

, (1.52)

где – действующее значение напряжения на вторичной обмотке трансформатора.

Из анализа выражений (1.6) и (1.52) следует, что в схеме мостового выпрямителя к вентилю обратное напряжение прикладывается вдвое меньше, чем в схеме выпрямителя с нулевым выводом.

Рассчитаем значения характерных мощностей и для мостового выпрямителя в соответствии с изложенной выше методикой. Вначале вычислим необходимые для расчета действующие значения токов и первичной и вторичной обмоток трансформатора для случая чисто активной нагрузки.

Поскольку токи первичной и вторичной обмотки имеют синусоидальную форму, действующее значение тока определим по величине действующего значения напряжения и сопротивлению нагрузки : . Выражая через действующее значение напряжения нагрузки (1.51), получим

. (1.53)

Действующее значение тока связано с известным соотношением:

, (1.54)

где – коэффициент трансформации трансформатора.

Действующему значению соответствует (1.51), действующее значение первичного напряжения в раз больше напряжения: : :

;

; (1.55)

.

Определим те же значения мощностей для случая активно-индуктивной нагрузки при . При таком условии форма переменных токов и является прямоугольной, для которой действующие значения токов и определяются из следующих соотношений с учетом знака тока :

;

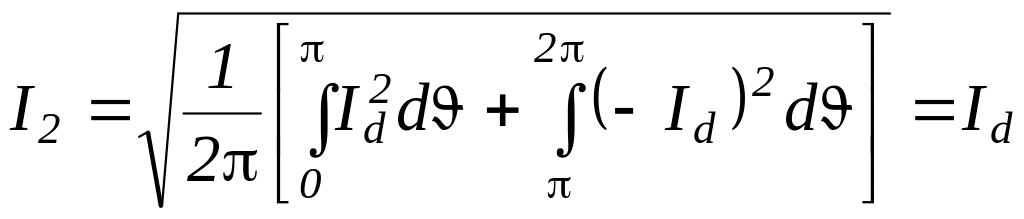. (1.56)

При известных выражениях действующих значений напряжений и , использованных при расчете мощностей (1.55), получаем следующие расчетные соотношения для вычисления мощностей для случая активно-индуктивной нагрузки:

;

; (1.57)

.