Раздел 6 Трёхфазные выпрямители 228

6.1. Трёхфазный выпрямитель с нулевым выводом 229

6.1.1. Работа выпрямителя при активной нагрузке 229

6.1.2. Работа выпрямителя при активно-индуктивной нагрузке 232

6.2. Трёхфазный мостовой выпрямитель 239

6.3. Трёхфазный мостовой управляемый выпрямитель 244

6.3.1. Учет коммутации в схеме трёхфазного управляемого выпрямителя 249

6.4. Энергетические характеристики трёхфазных выпрямителей 252

6.5. Преобразователь частоты с непосредственной связью 254

КОНТРОЛЬНЫЕ ВОПРОСЫ 262

ЗАКЛЮЧЕНИЕ 262

РЕКОМЕНДУЕМЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК 264

Введение

Локомотивное хозяйство железных дорог России является самым крупным потребителем электрической энергии. Только на тягу поездов ежегодно расходуется до 83 % электроэнергии, потребляемой всем железнодорожным транспортом. Снижение энергоемкости перевозочного процесса и повышение энергетической эффективности электроподвижного состава становится актуальной задачей. Программа «Энергетическая стратегия железнодо­рожного транспорта принята на период до 2010 г. и на перспективу – до 2020 года» ОАО «РЖД». Ее целью является полное и надежное энергообеспечение перевозочного процесса при минимизации энергетических составляющих себестоимости перевозок.

В локомотивном хозяйстве планируется внедрить технические решения, направленные на повышение энергетической эффективности, в частности бесколлекторный тяговый электропривод с современными полупроводниковыми преобразователями, а также устройства компенсации реактивной мощности. В целях улучшения показателей использования локомотивов предусматривается улучшение качества потребляемой энергии, при котором ожидается ее экономия до 3 %.

Квалифицированный специалист должен в совершенстве знать процессы преобразования энергии на подвижном составе, осуществляемые с помощью современных электронных устройств. Основой современных технологий является силовая и информационная электроника. С появлением новых, полностью управляемых силовых полупроводниковых приборов, расширилась область их применения, самой большой и важной частью которой является электропривод. Кроме того, современная полупроводниковая техника послужила основой для появления принципиально новых устройств, позволяющих значительно улучшить качество потребляемой энергии.

Целью этого пособия является углубление знаний студента в направлении развития электронной и преобразовательной техники. Полученные знания явятся основой для разработки и внедрения на предприятиях транспорта новых преобразователей, а также устройств, улучшающих качество электропотребления.

Раздел 1 неуправляемые выпрямители

Рекомендуемая литература: [2, 3, 10, 12].

1.1. Однофазный выпрямитель с нулевым выводом

1.1.1. Работа выпрямителя при активной нагрузке

В

Рис. 1.1. Однофазный выпрямитель с нулевым выводом при активной нагрузке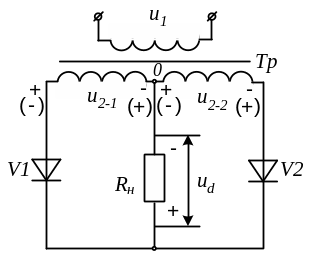

ыпрямитель (рис. 1.1) состоит из понижающего трансформатора , вторичные обмотки которого соединены с анодами вентилей и . Сопротивление нагрузка включено между общей точкой соединения катодов вентилей и средним (нулевым) выводом обмотки трансформатора.

Схема соединения обмоток трансформатора такова, что напряжения вторичных обмоток и сдвинуты на 180 эл. град относительно нулевого вывода трансформатора, т. е. мгновенные значения напряжений, поступающих на аноды вентилей и , равны по величине и противоположны по знаку.

Рассмотрим принцип действия выпрямителя для случая чисто активной нагрузки . Вентили выпрямителя принимаем идеальными, т. е. прямое падение напряжения в проводящем состоянии и обратный ток закрытого вентиля равны нулю. Диаграммы, поясняющие работу выпрямителя, представлены на рис. 1.2, а, б, в, г, д, ж.

На интервале , соответствующем положительной полуволне сетевого напряжения , во вторичных обмотках трансформатора действуют положительное напряжение и отрицательное напряжение относительно нулевого вывода трансформатора, имеющего нулевой потенциал. Полярность этих напряжений показана на рис. 1.1 без скобок. Поскольку к аноду вентиля  прикладывается напряжение положительной полярности, он переходит в проводящее состояние, а вентиль закрыт обратным для него отрицательным напряжением . Мгновенная схема замещения, соответст­вующая описываемому интервалу времени , представлена на рис. 1.3. Утолщенной линией на рисунке показан контур протекания тока нагрузки , а тонкой линией – та часть схемы, в которой ток отсутствует.

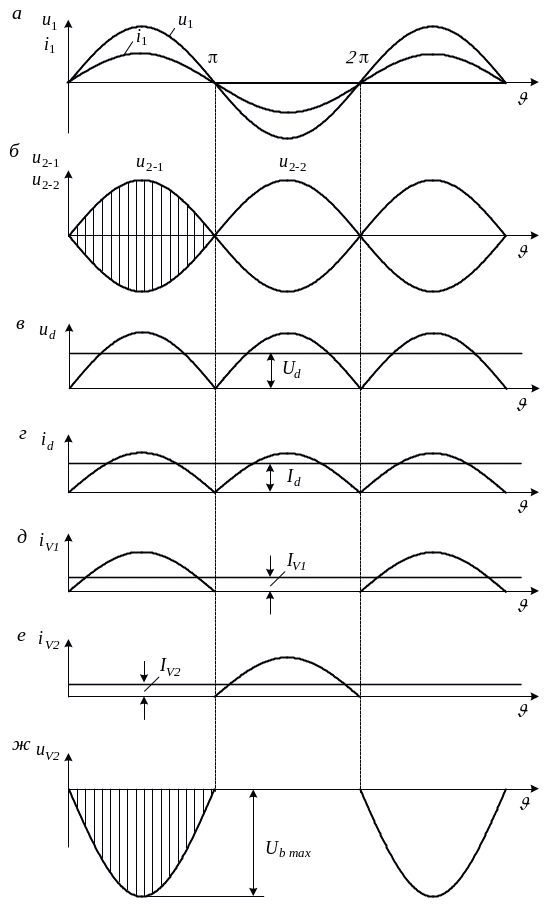
Рис. 1.2. Диаграммы работы выпрямителя при активной нагрузке

И

Рис. 1.3. Схема замещения преобразователя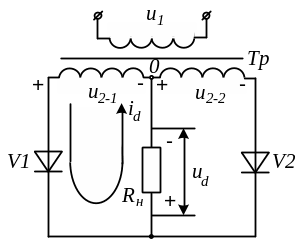

з рис. 1.3 следует, что при нулевом падении напряжения на вентиле все напряжение вторичной обмотки трансформатора прикладывается к нагрузке . В этом случае форма напряжения на нагрузке (рис. 1.2, в) повторяет напряжение (рис. 1.2, б). Полярность напряжения нагрузки также определяется полярностью напряжения . Поскольку напряжение , измеренное относительно нулевого вывода трансформатора, имеет положительную полярность, кривая показана в виде положительной полуволны напряжения на рис. 1.2, в. Ток в цепи нагрузки определяется величиной приложенного к ней напряжения = и сопротивлением нагрузки , т. е. . Для случая чисто активной нагрузки форма протекающего через нее тока (рис. 1.2, г) повторяет форму напряжения нагрузки . Ток нагрузки (рис. 1.3) замыкается через открытый вентиль , вторичную обмотку трансформатора и сопротивление нагрузки . Поскольку контур тока является замкнутым и неразветвленным, мгновенные значения тока вентиля составят . В этой связи на интервале диаграмма тока вентиля (рис. 1.2, д) повторяет форму тока нагрузки (рис. 1.2, г).

Выясним с помощью рис. 1.3 форму напряжения на вентиле , который на интервале находится в закрытом состоянии. Напряжение на определяется разностью потенциалов его катода и анода. На анод поступает отрицательное напряжение вторичной обмотки трансформатора, а к его катоду прикладывается положительное напряжение через открытый вентиль . При нулевом падении напряжения на всё напряжение поступает на катод вентиля .

Таким образом, вентиль находится под обратным напряжением двух обмоток трансформатора, мгновенные значения обратного напряжения на определяется разностью ординат кривых напряжений и (рис. 1.2, б), поступающих, соответственно, на его катод и анод. Перенося отрезки прямых рис. 1.2, б на рис. 1.2, ж и соединяя их плавной линией, получим кривую напряжения на вентиле на интервале .

Во втором полупериоде  – 2 работы преобразователя полярность напряжения вторичных обмоток меняется на противоположную, что показано в скобках (рис. 1.1). Вентиль переходит в открытое состояние под действием положительного напряжения , а вентиль закрывается отрицательным напряжением . К нагрузке через открытый вентиль прикладывается напряжение той же полярности, что и на ранее рассмотренном интервале 0 – . В этой связи на интервале  – 2 напряжение (рис. 1.2, в) показано в виде положительной полуволны напряжения, мгновенные значения которого повторяют форму напряжения (рис. 1.2, б).

Таким образом, к нагрузке прикладываются однополярные полуволны напряжения, определяемые формой напряжения вторичных обмоток трансформатора. В этом заключается принцип процесса выпрямления, при котором из переменного напряжения вторичных обмоток трансформатора формируются одинаковые по знаку положительные полуволны напряжения на нагрузке. В остальном электромагнитные процессы на интервале  – 2 не отличаются от процессов, рассмотренных в первом полупериоде .

Определим основные соотношения между токами и напряжениями в схеме выпрямителя, принимая за исходные параметры действующее напряжение  вторичной обмотки трансформатора и сопротивление нагрузки .

Напряжение на нагрузке определяется средним значением полуволн выпрямленного напряжения . Кривая на интервале повторяемости Т =  (0 – ,  – 2 …) повторяет форму напряжения вторичной обмотки трансформатора и описывается выражением

, (1.1)

где – действующее значение напряжения на обмотке трансформатора; – амплитудное значение напряжения на обмотке трансформатора.

Среднее значение напряжения за период Т =  определяется по формуле

. (1.2)

Для получения заданного значения выпрямленного напряжения по (1.2) можно рассчитать необходимое для этого действующее значение напряжения вторичной обмотки трансформатора:

. (1.3)

Среднее значение тока нагрузки (рис. 1.2, г) определяется приложенным к ней напряжением и сопротивлением нагрузки :

. (1.4)

Поскольку ток нагрузки замыкается через цепь вентилей , поочередно, среднее значение тока, протекающего через один вентиль , вдвое меньше среднего значения тока нагрузки :

. (1.5)

Выше было установлено, что к закрытому вентилю выпрямителя прикладывается обратное напряжение , определяемое суммарным напряжением обмоток трансформатора: . Амплитудное значение обратного напряжения вентиля равно, соответственно, сумме амплитудных значений напряжений обмоток трансформатора:

, (1.6)

где – амплитудное напряжение обмотки трансформатора.

Определим мощности первичной и суммарную мощность вторичных полуобмоток трансформатора , а также его типовую мощность . Расчетные мощности обмоток трансформатора и находим как произведение действующих значений напряжения на обмотке и протекающего через нее тока. Типовая мощность трансформатора определяется полусуммой мощностей и обмоток:

; ; , (1.7)

где и – действующие значения напряжений первичной и вторичной обмотки трансформатора; и – действующие значения токов первичной и вторичной обмотки трансформатора.

Значения мощностей выразим по величине мощности цепи выпрямленного тока: . При расчете используем известные соотношения, связывающие действующие значения напряжений и токов первичной и вторичной обмотки трансформатора:

; ( – коэффициент трансформации трансформатора), а также в общем виде соотношения для амплитудных и действующих соотношений напряжений и токов

; .

Действующее значение тока первичной обмотки , необходимое для расчета мощности , определим по амплитудной величине тока вторичной обмотки и коэффициенту трансформации трансформатора :

. (1.8)

Амплитудное значение тока вторичной обмотки трансформатора определяется отношением амплитудного значения напряжения обмотки и сопротивления нагрузки :

. (1.9)

Выражая напряжение в (1.9) через известное соотношение (1.3), а также принимая во внимание формулу (1.4), для тока I_2m получим следующее выражение:

. (1.10)

Подставляя полученное значение тока в (1.8), получим искомое выражение для действующего значения тока первичной обмотки трансформатора :

. (1.11)

Действующее значение тока вторичной обмотки трансформатора рассчитаем в соответствии с известным выражением для действующего значения периодической функции [1, 2].

. (1.12)

Ток вторичной обмотки трансформатора на интервале ( ) определяется током вентиля (рис. 1.2, д, е). Поскольку ток протекает через обмотку трансформатора только в течение одного полупериода, интегрирование тока по (1.12) осуществляется в пределах 0–. На интервале проводимости вентиля ток вторичной обмотки описывается выражением

, (1.13)

где – амплитудное значение тока.

С учетом выражения (1.9) уравнение (1.13) принимает вид

. (1.14)

Подставляя выражение (1.14) в уравнение (1.12) и осуществляя преобразование с учетом (1.4) и формулы неопределенного интеграла

, (1.15)

получим расчетную формулу для тока :

. (1.16)

Выразим входящие в формулу (1.7) действующие значения напряжений первичной и вторичной обмоток трансформатора через величину действующего значения напряжения на нагрузке . Значения и связаны соотношением (1.3). Подставляя в формулу (1.7) выражения (1.3) и (1.16) для расчета , с учетом , получим выражение для суммарной мощности вторичных обмоток трансформатора:

. (1.17)

Аналогично получим выражение для расчета мощности первичной обмотки путем совместного решения уравнений (1.3) и (1.11):

. (1.18)

Типовая мощность трансформатора рассчитывается по известным значениям мощностей его обмоток и [10]:

. (1.19)

Для оценки эффективности работы того или иного преобразователя необходимо определить его энергетические характеристики. Одним из основных показателей, характеризующих качество потребляемой энергии, является коэффициент мощности преобразователя. Он показывает степень потребления выпрямителем производительной активной мощности. Снижение коэффициента мощности сопровождается увеличением потребления преобразователем реактивной мощности и загрузки системы электроснабжения непроизводительным реактивным током. Протекание 1А реактивного тока в тяговой сети переменного тока вызывает в 5–7 раз большие потери напряжения по сравнению с активным током. Величина потерь напряжения в контактной сети составляет в среднем 2,4–4 кВ, это на 80 % обусловлено потреблением электровозом реактивной мощности [9]. Эти показатели подтверждают необходимость анализа рассматриваемых энергетических показателей преобразователей и выбора возможных путей их улучшения.

В общем виде для коэффициента мощности справедливо соотношение [10]

, (1.20)

где φ – угол сдвига основной гармоники потребляемого тока по отношению к питающему напряжению; – коэффициент искажения формы потребляемого тока, определяемый отношением первой гармоники тока к его действующему значению .

Из (1.20) следует, что для повышения следует приближать фазу потреб­­ляемого тока к питающему напряжению, а также улучшать форму этого тока.

Коэффициент мощности преобразователя характеризуется также отношением активной и полной потребляемых мощностей и рассчитывается как для синусоидальных, так и для несинусоидальных цепей по общей формуле:

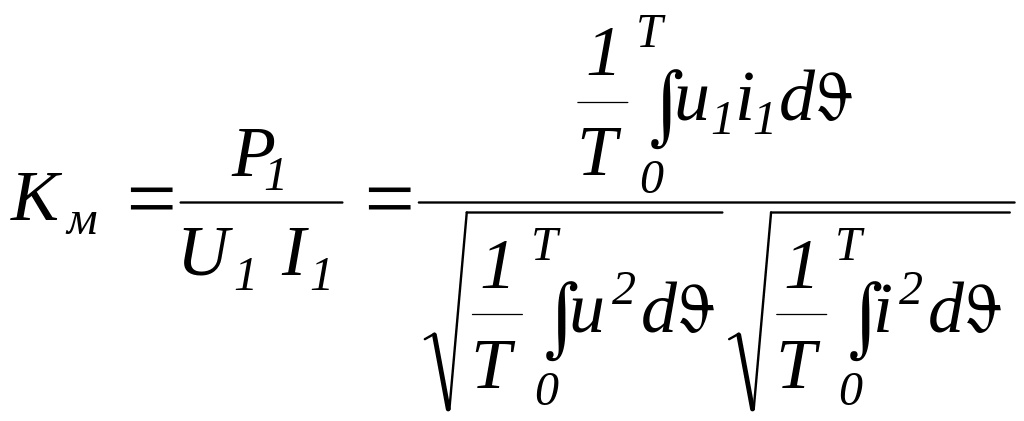, (1.21)

где , – мгновенные значения напряжения и тока первичной обмотки трансформатора; – действующие значения напряжения и тока первичной обмотки трансформатора.

Рассчитаем по формуле (1.21) величину коэффициента мощности однофазного выпрямителя, работающего на активную нагрузку. Диаграммы напряжения и тока первичной обмотки трансформатора показаны на рис. 1.2, а. Напряжение и ток имеют синусоидальную форму, для которой амплитудные и действующие значения напряжения и тока связаны соотношением: ; . Кривые входного напряжения и тока описываются выражениями:

; . (1.22)

Величину активной мощности рассчитаем в соответствии с выражением числителя (1.21), используя выражение (1.22) для мгновенных значений :

. (1.23)

С учетом (1.15) для активной мощности получим

. (1.24)

Подставив полученное выражение в (1.21), получим

. (1.25)

Таким образом, коэффициент мощности однофазного выпрямителя, работающего на активную нагрузку, имеет наибольшее значение: =1. В соответствии с (1.20) это объясняется тем, что фаза потребляемого тока совпадает с питающим напряжением ( = 0, cos  = 1), а для синусоидальной формы кривой тока коэффициент искажения формы тока (1.20) υ =1.