МММ

На доске написано следующее выражение

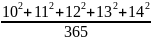
В позапрошлом веке крестьянские дети в сельской школе умели решать такие задачки в уме. Тому, кто не сможет в уме решить эту задачу, читать дальнейший текст бесполезно. Лучше уж сразу в сельскую школу на доучивание!

Раздел 1. Общие принципы построения математических моделей

Теоретические занятия (лекции) – 6 часов.

Лекция 1. Информационная. Рассматриваются общие принципы построения математических моделей. Вводятся классификации математических моделей по различным признакам. Рассматриваются примеры математических моделей двигателей летательных аппаратов и их элементов. Объясняются иерархические принципы построения сложных математических моделей. Рассматриваются взаимосвязи между различными моделями. Показывается цикл формирования математической модели двигателя или его элемента.

Классификация математических моделей. Регулярные и численные математические модели. Аналитические математические модели. Детерминированные и статистические математические модели. Математические модели идентификации. Особенности каждого класса математических моделей.

Геометрическое представление математических моделей. Кривые и поверхности отклика. Использование топографической проекции для изображения двумерных (многомерных) поверхностей отклика. Области допустимых значений. Ограничения 1-го и 2-го рода.

Унимодальные одномерные и многомерные модели. Частные виды унимодальных моделей.

Иерархические принципы построения математических моделей сложных систем. Принципы декомпозиции математических моделей. Пример иерархической структуры математической модели сложной системы (например, ЭСУ космического аппарата). Характеристики математических моделей, расположенных на различных уровнях иерархической структуры.

В рамках данного курса предполагается изучение методов математического моделирования двигателей летательных аппаратов. Задача совершенно необъятная. Хотя бы потому, что существует множество разнообразных типов двигателей с совершенно разными принципами работы, конструктивными особенностями, физическими процессами и т.д. Подробное рассмотрение всевозможных вариантов не представляется возможным в разумные сроки. Но базовые принципы и некоторые методы реализации математических моделей двигателей и их элементов рассмотреть можно. Вот этим и займемся.

Чтобы разобраться в том, что нам предстоит, рассмотрим стоящие перед нами задачи. Для начала проанализируем фразу «методы математического моделирования двигателей летательных аппаратов». Начнем с конца, то есть с «летательных аппаратов». Прежде, чем моделировать какой-то двигатель, необходимо понять какие требования к нему выдвигаются. А эти требования определяются летательным аппаратом и могут быть самыми разнообразными. Начиная с типичных (тяга, масса, геометрические размеры, расход топлива) и вплоть до заметности в радио- и инфракрасном диапазоне с определенного ракурса. Откуда и как эти требования берутся? Разработчики летательных аппаратов исходя из своих целей (опять же спущенных откуда-то, то ли из отдела маркетинга, то ли из постановления правительства) решают ряд вопросов. Сначала идут вопросы связанные с выбором. Какие двигатели им нужны: поршневые, турбовинтовые, реактивные одно- или двухконтурные? Сколько двигателей поставить и где? Затем начинается формулировка требований к двигателю. На этом этапе как раз и появляется тот перечень, который я упомянул выше. А дальше как правило возникают новые вопросы, когда двигателисты начинают в ходе разработки рассматривать различные варианты. Например, мы можем уменьшить расход топлива за счет увеличения массы двигателя. При каком соотношении этих двух параметров это окажется выгодным с точки зрения летательного аппарата? Особенно такие взаимодействия сказываются на гиперзвуковых аппаратах, где корпус самолета выполняет отчасти роль воздухозаборника и сопла.

Теперь перейдем к двигателям. Тут мы тоже видим сходный набор задач. Сначала идет выбор из некого набора вариантов. Например, вариантов компоновок, выбор материалов и т.п. Затем выработка требований к отдельным элементам конструкции. На последующих этапах возникают вопросы целесообразности внесения изменений и уточнений в задания на разработку отдельных элементов. Как правило, сходный набор задач возникает и если мы опустимся на уровень разработки элементов конструкции.

Далее (ранее) у нас слова идут «математическое моделирование». Смысл вроде бы понятен, но на некоторые нюансы все же стоит обратить внимание. Сами по себе математические модели не представляют никакой ценности. Если враг стоит у ворот, то бесполезно рассказывать ему, что согласно вашей гениальной математической модели нападение на вас противоречит его собственным интересам. Нужны вооруженные силы с самолетами и ракетами, для которых нужны вполне реальные двигатели. Гражданские авиакомпании тоже не будут в восторге от рассказов о математических моделях идеальных двигателей. Они будут платить только за вполне реальные, пусть даже с отдельными недостатками. Поэтому все модели (не только математические) имеют смысл, только если они полезны для разработки конкретного «железа». В обозримом будущем это «железо» по прежнему в процессе создания будет проходить через натурные испытания (пусть даже ускоренные, сокращенные или какие-то иные). Следовательно, математическое моделирование оправдано, если оно сокращает объем этих испытаний. Отсюда вытекает ряд требований к математическим моделям. Во-первых, они должны быть точными. Точность должна быть по крайней мере сопоставима с точностью эксперимента. Иначе объем испытаний не уменьшится. От повышения точности, казалось бы, будет только лучше. Но не всегда. И тут мы приходим ко второму требованию: затраты ресурсов (как материальных, так и времени) на математическое моделирование должны быть меньше, чем на проведение эксперимента. Никто не будет годами ждать результатов расчета, если за это время все можно проверить экспериментально. Поэтому простые (пусть даже не слишком точные) математические модели часто оказываются гораздо более полезными, чем точные, но сложные.

Ну и наконец, доберемся до «методов». Их количество не меньше, чем число решаемых задач. Не существует даже общепризнанной классификации методов математического моделирования. Этот факт не удивляет хотя бы потому, что не существует даже общепризнанной классификации решаемых задач. К тому же очень часто границы между различными задачами и методами размыты. Тем не менее один из возможных вариантов классификации мы здесь рассмотрим. Начнем с упомянутых выше задач. Во-первых, сразу можно отметить, что с точки зрения математики они делятся по конечному результату на два типа: дискретные и непрерывные. К первому типу относятся задачи выбора из некоторого набора вариантов (например, выбор компоновки). Ко второму задачи, где множество возможных результатов непрерывно: масса, тяга, размеры, поля скоростей, температур и т.д. Границы между этими типами тоже не очень четкие. Например, число ступеней компрессора может меняться только дискретно. Но для его определения можно придумать непрерывно меняющуюся функцию, чей результат потом будем округлять до ближайшего (большего) целого. Вообще говоря, дискретные алгоритмы – это отдельное направление математики и довольно интересное. Но при разработке двигателей редко встречаются сложные задачи этого класса (например, выбор из очень большого числа вариантов). Поэтому в этом курсе мы отведем им минимум места. Основное время мы отведем задачам, где входные и выходные параметры определены на непрерывных множествах.

Далее смотрим на следующую группу задач, связанную с формированием требований. На этом этапе нам нужно научиться рассчитывать параметры некого целого (летательный аппарат, двигатель, элементы конструкции) на основе данных о его составных частях. А также решать обратную задачу: при каких значениях входных параметров мы получим заданные результаты на выходе. Тут могут применяться разные подходы. Можно моделировать физические процессы, проходящие в рассматриваемом устройстве. В литературе такие методы иногда называют регулярными. Можно считать рассматриваемое устройство «черным ящиком», содержимое которого нам на данном этапе не очень интересно, главное установить зависимость выходных параметров от входных. Такие модели в литературе иногда называются моделями идентификации. В инженерном деле широко применяется промежуточный подход: учитывается часть физических процессов (как в регулярных моделях), а остальное считается как в методах идентификации. Такие модели иногда называются полуэмпирическими.

В свою очередь регулярные математические модели делятся на аналитические и численные. В аналитических моделях редко удается получить аналитическое решение. Если все же это удалось, то модель называют аналитически разрешимой. Чаще аналитическими методами удается лишь упростить задачу, а окончательный ответ приходится получать численно. Такие модели называют численно разрешимыми. Численные модели делят на детерминированные и статистические. В первом случае предполагается однозначная зависимость между входными и выходными параметрами. Во втором предполагается лишь вероятностная оценка. При этом на вход тоже часто подаются не значения переменных, а некие законы их распределения.

Часто численные методы классифицируют еще и по форме описания используемых в ходе решения функций. По этому признаку их можно разделить на линейные, квадратичные и т.п.

Модели идентификации могут строится на основе экспериментов (эмпирические модели) или на основе расчетов, построенных по другим моделям. Данные для них могут приходить из каких-то неконтролируемых составителем модели источником. Тогда говорят о «неорганизованном эксперименте». А можно поставить задачу о получении максимальной точности при минимальном количестве экспериментов. В этом случае имеем задачу об оптимальном планировании эксперимента.

Существует и еще одна своеобразная группа методов – аналоговое моделирование. Суть этих методов сводится к подмене одних объектов (физических процессов или устройств) на другие, но со схожей математической моделью.

Ну и вне предложенной классификации осталась группа методов, связанная с оценкой адекватности математических моделей.

А теперь еще раз вернемся к тем задачам, которые приходится решать. Там у нас еще остались нерассмотренными вопросы о взаимовлиянии системы с подсистемами (летательный аппарат с двигателем, двигатель со своими агрегатами и т.п.). Они приводят к необходимости оптимизации системы. Тут мы тоже имеем множество разнообразным математических моделей. Их классификация сходна с классификацией регулярных моделей.

Построив таким образом некую классификацию математических моделей мы несколько забыли о требовании экономии ресурсов. Если бы этого требования не было, то мы вполне могли бы ограничится всего одним классом моделей: взяли бы систему уравнений для описания основных физических процессов (уравнения Навье-Стокса, теплопередачи, напряженности в твердых телах и т.п), заложили все геометрические и прочие данные и посчитали бы сразу весь двигатель. Звучит очень заманчиво, но даже для современных суперкомпьютеров такая задача является слишком тяжелой. То есть это или невозможно, или слишком долго и дорого. А считать надо. Значит, начинаем разбивать исходную задачу на серию более простых.

При моделировании сложных систем существует способ, который часто дает большую экономию: иерархическое построение моделей. Если сложную систему насколько возможно раздробить и потом проследить за получающимися связями, то мы почти всегда увидим, что они распределяются крайне неравномерно. То есть образуются некие кластеры, внутри которых связей много, а с другими кластерами мало. Соответственно, можно создать модели для таких кластеров. Если кластеров много, то они как правило тоже собираются в некие скопления, слабо связанные между собой. Значит, можно создавать модели для таких скоплений. Чем сложнее была исходная система, тем больше уровней можно построить таким образом. В технических системах это легко прослеживается, так как иерархический подход существенно облегчает разработку и модернизацию. В результате получаем что-то вроде: летательный аппарат – двигатель – агрегат – элемент конструкции – физический процесс. Причем на каждом уровне интересны свои процессы, а подробностями строения подсистемы и надсистемы можно пренебречь, достаточно задать законы их взаимодействия. Это и позволяет существенно упрощать математические модели.

Например, можно разделить отдельные физические процессы. То есть отдельно проводить прочностные расчеты, отдельно газодинамические и т.д. Можно делить по геометрическому принципу. Например, если на одной ступени компрессора имеем много одинаковых лопаток, то вовсе необязательно считать их все. Достаточно посчитать одну. Можно пойти еще дальше. Вязкость оказывает существенное влияние только в пограничном слое. Из этого следует, что можно иметь одну модель для невязкого течения между лопаток и другую для пограничного слоя. Но при делении большой задачи на мелкие нельзя забывать об их взаимовлиянии. Например, результаты газодинамического расчета будут влиять на тепловые, те в свою очередь на прочностные и т.д. То есть если мы где-то проводим искусственную границу, то нужно иметь какую-то модель взаимодействия полученных отдельных частей.

Теперь несколько слов о графической интерпретации стоящих перед нами задач. Задача выбора из дискретного множества обычно визуализируется с помощью так называемых графов. Графом называется множество точек (вершин графа), соединенных между собою линиями или стрелками. Обычно вершинами графа изображают возможные варианты, а линиями – возможные переходы между ними.

Но нам чаще придется иметь дело с функциями, определенными на непрерывном множестве. Наглядная графическая интерпретация при этом возможна для случаев функции от одного и двух аргументов. В первом случае мы получим типичный график функции, во втором удобнее использовать так называемые «геодезические линии».

Введем сразу же некоторые термины, которыми мы будем пользоваться в нашем курсе. Множество точек, задаваемых рассматриваемой функцией называют поверхностью отклика. Для задач оптимизации важным является количество экстремумов в рассматриваемой области. В зависимости от числа минимумов или максимумов (в зависимости от постановки задачи) функции могут быть унимодальными (один оптииумум) или полимодальными. Функция в общем случае может быть и недифференцируемой. Она может иметь разрывы. Для нахождения оптимумов недифференцируемой функции очень полезным бывает свойство выпуклости. Выпуклой называется функция, если в каждой ее точке можно провести секущую такую, что все значения функции (кроме точки пересечения) лежат по одну сторону от секущей.

Далее рассмотрим вопрос о выборе модели или создании новой (на случай, если готовой подходящей не оказалось). Прежде, чем браться за решение какой-либо задачи, необходимо правильно поставить задачу¹. Для этого, прежде всего, рекомендуется получить ответ на следующие вопросы:

- Что нужно получить в конечном итоге?

- С какой точностью нужно получить результат?

- Какие ресурсы выделяются на решение задачи?

- Нельзя ли упростить задачу или свести ее к более простым?

Как помочь человеку, который не знает, что ему нужно, рассматривается в других курсах (например, по психологии). В случае четко сформулированной цели дальнейшие действия определяются ответами на вопросы о точности, ресурсах и возможности упрощения задачи.

Ответы на перечисленные выше вопросы, как правило, сводят к минимуму выбор методов, которыми может быть решена поставленная задача. С учетом предельной краткости данного курса, вероятно, несчастный читатель найдет здесь не более одного подходящего для его случая метода. Если известно несколько методов решения задачи, то выбирать следует тот, который привычнее.

Прежде, чем моделировать какое-либо устройство нужно провести ранжировку процессов. Нужно составить список всех значимых процессов. Обычно составляется сначала список всех процессов, которые потенциально могут оказаться значимыми. Затем проводятся оценки характерных значений физических величин, которые фигурируют в описаниях этих процессов². На основании этих данных оценивают погрешность, которую даст неучет каждого процесса, и сравнивают ее с желаемой погрешностью (см. Вопросы поставленные в начале). По этим данным принимают решение – какие процессы учитывать, а какие нет. Вообще говоря, существуют критерии о включении/не включении процессов в итоговый список. Например,

• сумма погрешностей отброшенных процессов должна быть меньше желаемой погрешности;

• сумма квадратов погрешностей отброшенных процессов должна быть меньше квадрата желаемой погрешности.

На практике, как правило, поступают проще: если оценка погрешности, получающаяся при отбрасывании какого-либо процесса, менее одной десятой от желаемой погрешности, то процесс отбрасывается, иначе – оставляется. Если какой-то процесс решено не учитывать, то полезно сформулировать условие, при котором его необходимо учитывать. Это позволит четко сформулировать область применимости той математической модели, которая будет составлена.

Теперь можно приступить к написанию системы уравнений и граничных и/или начальных условий, а также ограничений. Начнем с конца. Всегда нужно помнить, что математика занимается числами, которые живут самостоятельной жизнью и физикой совершенно не интересуются. Поэтому, с точки зрения математики, нет ничего страшного в отрицательных плотностях и абсолютных температурах. Если подобные вещи неприемлемы с точки зрения физики, то необходимо либо внести соответствующие ограничения в математическую модель, либо доказать, что в данном случае ничего страшного не произойдет. Обычно, легче поставить ограничения. Но на этом фокусы не кончаются. Сюда же следует включить как ограничения те условия, при которых следует учитывать неучтенные процессы.

При моделировании магнитных полей часто приходится учитывать, что рассчитываемое поле выходит за пределы устройства, в котором оно применяется. Приходится увеличивать расчетную область и ставить условия «на бесконечности». При моделировании двигателя аналогичная ситуация возникает на входе (воздухозаборник) и выходе (сопло) из двигателя. Но в большинстве инженерных задач расчетная область ограничена стенками. Часто характерные размеры для процессов, идущих в пристеночных (приграничных) областях, много меньше, чем характерный размер устройства. Это приводит к неприятному факту: если одними уравнениями описывать и процессы, проходящие в объеме, и процессы, проходящие вблизи границы, то задача становиться совершенно нерешабельной. Эту неприятность обычно обходят, разбивая задачу на две более простые: описание процессов только тех процессов, которые существенны в основном объеме, и описание приграничных областей (там, как правило, можно рассмотреть гораздо более простую с точки зрения геометрии задачу). При этом для решения этих двух задач могут использоваться принципиально различные подходы. Часто в объеме рассчитываются уравнения, моделирующие соответствующие процессы, а в качестве граничных условий используются полуэмпирические соотношения.

По сути, построение физико-математической модели после прохождения всех перечисленных выше этапов закончено. Но конечной целью, обычно, является не построение модели, а расчет конкретных параметров устройства. Прежде, чем приступить к реализации численного метода, как правило, нужно сделать еще несколько манипуляций.

• Во-первых, нужно посмотреть, нельзя ли воспользоваться еще чем-нибудь для упрощения расчетов. Например, наличие симметрии может в разы сократить объем вычислений.

• Во-вторых, для использования некоторых численных методов полезно записать уравнения какой-либо иной системе координат или в другом виде. Например, для метода конечных разностей желательно иметь так называемую «дивергентную» форму записи уравнений.

• В-третьих, если возможно введение потенциала какой-либо величины (что часто бывает, если можно пренебречь процессами вязкости и теплопроводности), то полезно бывает написать уравнения для потенциала (часто такие уравнения решаются с меньшими затратами ресурсов).

• Далее проверить, нельзя ли разбить задачу на несколько независимых. Например, если магнитное поле, создаваемое токами в плазме, много слабее поля, создаваемого внешней магнитной системой, то его можно рассчитывать независимо от расчета параметров плазмы.

• Наконец, в исследовательских задачах, часто бывает полезным записать уравнения в безразмерном виде. Это позволяет выявить (если до сих пор почему-то не были известны) параметры подобия, лишний раз проверить правильность модели и, в ряде случаев, избавиться от некоторых численных проблем.

Лекция 2. Информационная. Объясняются статистические методы проверки адекватности математических моделей. Излагаются основные положения теории проверки моделей. Рассматриваются критерии согласия хи-квадрат и Смирнова-Колмогорова, критерий Фишера. Объясняются заложенные в них принципы и области их применимости.

Датчики случайных чисел и их использование при статистическом моделировании.

Равномерное распределение случайных величин. Плотность распределения случайных величин. Использование равномерно распределенных случайных величин.

Равномерное распределение случайных величин. Формулы и график плотности распределения.

Нормальный закон распределения случайных величин. Плотность вероятности для нормально распределенных случайных величин. Что такое математическое ожидание и среднее квадратичное отклонение при нормальном распределении случайной величины? Почему нормальный закон распределения случайных величин часто встречается при изучении природных явлений? Где этот закон применять нельзя?

Экспоененциальное распределение случайных величин. Для решения каких задач используется экспоненциальное распределение.

Г – распределение случайных величин. Какие процессы описываются Г- распределением? Смысл и ограничения для всех параметров Г-распределения.

Постановка задачи доказательства адекватности математической модели действительности (верификация математических моделей). Пути верификации математических моделей. Использование статистических данных. Формулировка гипотез Н₀ и Н₁. Парадигмы Пирсона-Неймана и Вальда. Общая схема процедуры проверки адекватности моделей. Критерии адекватности. Параметрические и непараметрические статистические критерии.

Критерии согласия. Критерий хи-квадрат Пирсона. Математический аппарат проверки адекватности математических моделей с помощью критерия хи-квадарат. Доверительная вероятность и толерантный интервал. Условия применимости критерия Пирсона.

Дисперсионные критерии для проверки адекватности математических моделей. Критерии Стьюдента и Фишера. Их математический аппарат. Условия использования дисперсионных критериев.

Сравнение конкурирующих математических моделей с помощью критериев Фишера и регуляризационного критерия несмещенности.

Непараметрические критерии адекватности математических моделей действительности. Критерий Колмогорова- Смирнова. Ранговый критерий Уилкоксона. Использование непрараметрических критериев при проверке адекватности математических модлей действительности.

Проверка адекватности математических моделей действительности с использованием критерия Вальда.

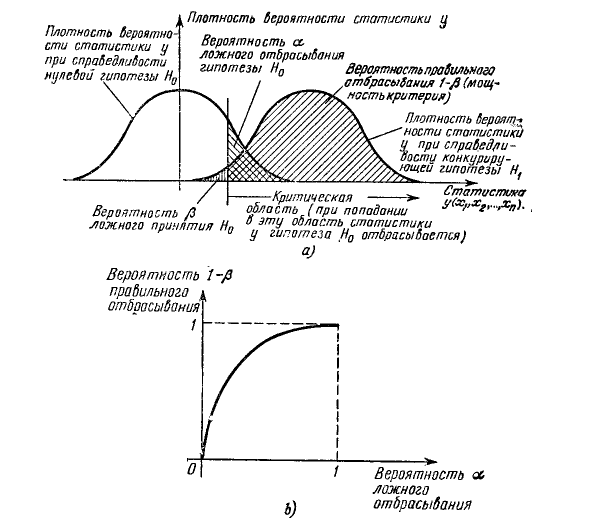
Риски «альфа» и «бета» при проверке адекватности математических моделей действительности и выбор значений этих рисков.

Изучение математических моделей начнем с конца. То есть с предположения, что уже есть готовая модель. Но прежде, чем ее применять, нужно ответить себе на вопрос об ее адекватности. То есть, а действительно ли она описывает то, что нужно, с требуемой точностью. Для этого нужно попробовать сравнить расчетные данные с экспериментальными. И тут мы неизбежно приходим к необходимости иметь дело со случайными величинами. Причем, случайными будут как расчетные, так и экспериментальные значения. Как минимум речь идет о погрешности расчетов и измерений, хотя источниками ошибок могут являться самые разнообразные процессы. Например, нельзя исключать человеческих ошибок при вводе информации. Отсюда уже следует потребность в достаточно большом объеме информации для сравнения. То есть по единичному сравнению нельзя делать однозначный вывод об адекватности (или неадекватности) модели. Вот тут мы и подошли к важному вопросу, который характерен для любых фильтров, то есть систем сортировки на «годных» и «не годных» по какому-то критерию (в данном случае на «адекватных» и «не адекватных»). Всегда возникают две возможные ошибки: отбраковать «годных» и пропустить «не годных». Часто их называют ошибками первого и второго рода. Конечно, очень хочется свести вероятности таких ошибок к нулю, но как правило это невозможно. Более того в большинстве практических случаев снижение вероятности одной из них приводит к повышению вероятности другой. Обычно допустимые вероятности ошибок назначаются волевым путем из каких-то внешних по отношению к рассматриваемой системе соображений. Например, для двигателя внешней системой (надсистемой) является летательный аппарат. Строго говоря, всегда следует контролировать вероятность ошибок обоего рода. То есть кроме случаев «адекватно» и «не адекватно» может возникнуть вариант «однозначный вывод сделать нельзя».

Прежде, чем заняться конкретными критериями оценки адекватности, рассмотрим несколько наиболее часто встречающихся в технике распределений вероятности случайных величин. В сложных системах почти никогда не встречается равномерное распределение. Оно типично лишь для отдельных процессов. Например, вероятность того, что птица попадет в воздухозаборник двигателя в данном месте, примерно равномерно распределена по площади миделя воздухозаборника. Как правило, в сложных системах (в том числе двигателях) приходится иметь дело с результатом действия многих процессов. Для них есть свои типичные распределения. Если наблюдаем несколько примерно одинаковых по своему воздействию независимых процессов (как вариант: результат многократного воздействия одного и того же процесса), то распределение будет близким к нормальному. В теории вероятности этот факт обосновывает центральная предельная теорема. На этом основании нормальное распределение использовалось почти повсеместно (то есть где надо и не надо). И в любом справочнике по статистике обязательно найдутся базирующиеся на этом распределении критерии оценки. Некоторые из них мы здесь рассмотрим. Нормальное распределение задается двумя параметрами: математическим ожиданием и дисперсией.

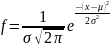
Но в сложных системах (в том числе и двигателях) как правило наблюдается иная ситуация. В серьез на это обратили внимание только в 60-х годах прошлого века. Поэтому до большинства учебников этот факт еще не добрался. Различных процессов много и их воздействие на конечный результат часто распределяется по степенному закону с отрицательным значением степени (распределение Парето). Например, турбулентность можно рассматривать как совокупность вихрей разного масштаба. Если мы построим распределение числа вихрей от их характерного размера, то получим как раз степенное распределение. Теоретически этот факт обосновал Колмогоров. Но у такого рода распределений есть свои особенности. В частности в природе не встречается объектов, для которых степенное распределение описывало бы происходящее во всем диапазоне какого-бы то ни было параметра. Обязательно «хвосты» распределения оказываются «обрезанными». Например, минимальный масштаб турбулентности определятся соответствует числу Рейнольдса порядка единицы. А максимальный масштаб для внутренних течений (типичных для двигателей) ограничивается размерами канала.

Но это мы обсудили влиятельность различных источников ошибок. А как при этом распределяются сами ошибки. Распределение тоже имеет колоколообразную форму, но описывается уже тремя переменными (третья связана со степенью в упомянутом степенном законе). К сожалению простой формулы тут не получается. Выходит неберущийся (в общем случае) интеграл (распределение Леви)

Формула

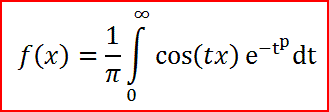
Но пару частных случаев, когда этот интеграл берется я тут приведу. Если параметр р=2, то получаем обычное нормальное распределение. Если р=1, то получаем распределение Коши, задаваемое формулой

Формула

У таких распределений есть очень неудобное свойство: при р<2 для них не определено понятие дисперсии, а для р<=1 не определено даже понятие математического ожидания. Строго говоря из-за того, что идеальных степенных распределений для источников не бывает, то получающиеся распределения плотности вероятности ошибок будут от описанных несколько отличаться и могут иметь и матожидание и дисперсию, но для каждого случая это нужно доказывать. Чем обычно пренебрегают. К чему приводит такое пренебрежение? Для ответа на этот вопрос сначала рассмотрим графики распределений.

Графики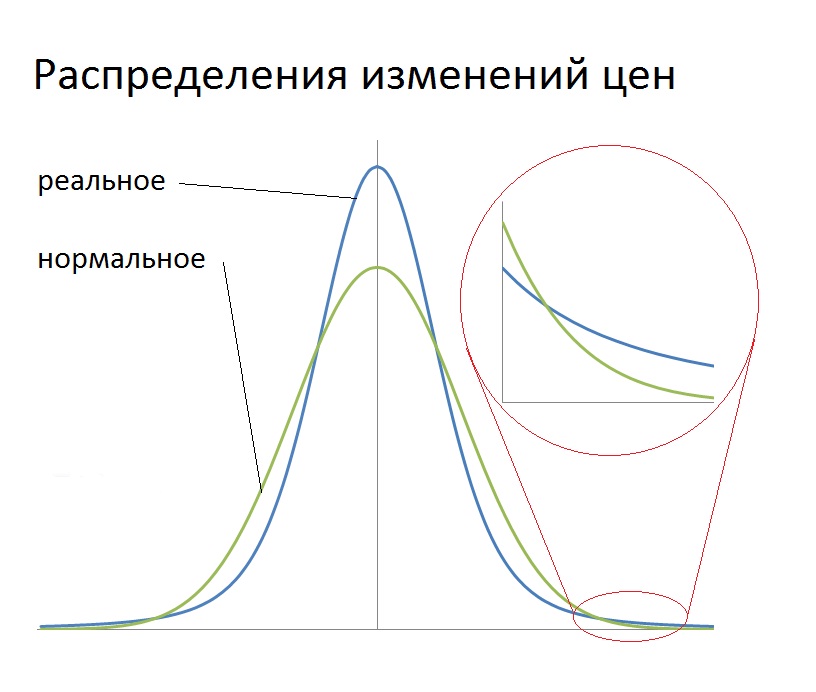

Как видим по сравнению с нормальным распределением получаются гораздо более «тяжелые хвосты». То есть вероятность получить большие отклонения оказывается гораздо больше (часто более чем на порядок), чем утверждает предположение о нормальности распределения. Тут следует также вспомнить, что в центральной предельной теореме использовалось предположение о независимости источников ошибок. В технике оно тоже часто нарушается и приводит к сходному влиянию на конечное распределение. Большие отклонения могут приводить к отказу отдельных подсистем, что в свою очередь сразу приводит к повышению нагрузки на другие подсистемы, что в свою очередь приводит к повышению вероятности их отказа и т.д. То есть народная мудрость «беда одна не приходит» справедлив и для технических систем (в том числе двигателей). Что в конечном итоге приводит опять же к «утяжелению хвостов» на графиках плотности вероятности ошибок. Об этом всегда следует помнить, особенно при расчетах, например, надежности.

И еще одно распределение, которое часто встречается в жизни и технике – экспоненциальное распределение. Оно характерно для процессов, равномерно расположенных во времени (слабо меняющихся с течением времени). Например, вероятность отказа двигателя в ближайшую минуту равна некой величине. Если в течение минуты отказа не произошло, то мы считаем, что вероятность отказа в следующую минуту остается примерно такой же. Плотность вероятности подобных событий как раз и описывается экспоненциальным законом

Формула

Теперь перейдем к вопросу об оценке адекватности модели. Предположим, что у нас имеется некоторый набор результатов экспериментов. С помощью математического моделирования мы попытались воспроизвести эти эксперименты и получили аналогичный набор результатов расчетов. Они не совпадают. Но этого и не требовалось. Как правило, нужно лишь, чтобы разница была небольшой (не превышала некоторую величину). И вот мы обнаруживаем, что в отдельных случаях это требование все же нарушается. Тут же встает вопрос: является ли это случайным отклонением (ошибка эксперимента, влияние посторонних возмущений и т.д.) или это неадекватность математической модели? Из самого вопроса следует необходимость рассмотрения двух гипотез. Одна утверждает, что модель адекватна, и нет достаточных оснований от нее отказываться. Другая, что модель не отвечает требованиям и должна быть отвергнута. На практике часто встречаются более интересные альтернативные гипотезы, но о них чуть позднее. Для принятия решения нужно сделать ряд предположений о распределении вероятности отклонений. То есть сначала построить некую математическую модель для ошибок и заняться вопросом ее адекватности. Для чего построить еще одну модель и т.д. Естественно, никто на практике подобные бесконечные цепочки не стоит и не собирается. Крайне редко можно увидеть два звена такой цепи. Обычно ограничиваются предположением о нормальном законе распределения со ссылкой на центральную предельную теорему. Для подтверждения или опровержения этой гипотезы часто данных не хватает. А на случай, если она окажется неверной, просто ужесточают критерии в надежде, что вероятность ошибки останется достаточно малой даже при ином законе распределения. Поэтому наиболее распространенные критерии проверки адекватности основаны на нормальном законе распределения ошибок.

Начнем с критерия χ² (он же критерий Пирсона). Он является наиболее распространенным критерием для проверки статистических гипотез. Этот критерий основан на расчете квадрата отклонения от рассматриваемой гипотезы и сравнении этого показателя с аналогичным для случайного отклонения. То есть для начала разбиваем все результаты на группы. В нашем случае таких всего две: с отклонением больше желаемого и меньше желаемого. В этом критерии фигурирует такое понятие как число степеней свободы. В нашем случае всего одна степень свободы: каждый результат может попасть или в одну группу, или в другую. Если бы у нас было бы большее число групп, то число степеней свободы было бы на единицу меньше, чем их число. Такой вариант обычно используется для проверок гипотез о заданном законе распределения.

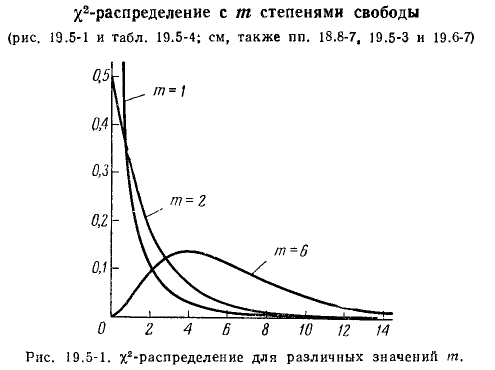
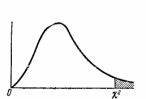
Однако вернемся к нашему случаю. Далее считаем величину χ² по формуле

где N – общее число измерений, Р – вероятности попадания в соотвтествующую группу. Наконец, нам понадобится установить допустимую вероятность ложного отбрасывания гипотезы, например 1%. Далее подразумевается следующий процесс. Предполагая, что отклонения от гипотезы распределены по нормальному закону, берутся «хвосты» распределения с заданной вероятностью ошибки. Для полученного распределения находится значение данного критерия. Естественно, нам это проделывать не нужно, ибо все уже давно посчитано и сведено в таблицы. Остается только сравнить наш результат с табличным. Если получилось больше табличного, значит скорее всего отклонения оказались больше, чем можно списать на случайность. Следовательно, гипотезу принять нельзя.

Другой широко распространенный критерий носит имена Смирнова и Колмогорова. Смирнов предложил, а позже Колмогоров обобщил идею. В отличие от предыдущего метода здесь учитывается не сумма квадратов отклонений, а наибольшее отклонение в функции распределения (не плотности вероятности, а именно вероятности). Например, для проверки соответствия экспериментального распределения теоретическому строим две функции распределения и находим максимальное расхождение. Полученное значение опять же сравнивается с табличным.

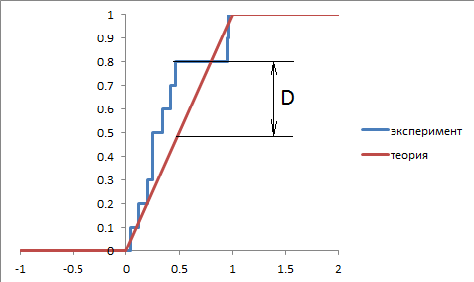
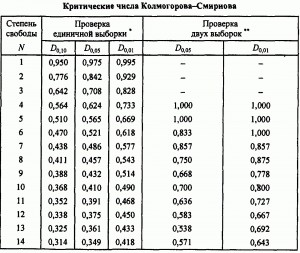
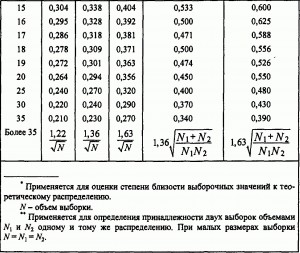
Для сравнения двух конкурирующих гипотез часто применяется тест (критерий) Фишера. Он основан на сравнении оценок дисперсий, полученных по разным гипотезам. В классическом виде рассчитывается отношение дисперсий

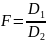
Принято в числителе помещать бОльшую дисперсию, чтобы значение принимало значение больше 1. Полученная величина сравнивается с табличным значением для заданных вероятностей ошибки и чисел степеней свободы для числителя и знаменателя. В русской версии Excel соответсвующая функция называется F.ОБР.ПХ и расшифровывается как обратное значение правостороннего распределения функции Фишера. Она показывает пороговое значение, выше которого с заданной вероятностью при нормальном распределении случайных величин соотношение дисперсий не поднимется. Соответственно, если мы получили меньшее значение критерия, то различия считаются статистически незначимыми.

На практике подход Фишера часто применяется к сравнению двух моделей. Если более сложная модель (использующая большее число параметров) дает меньшую оценку пограшности, то встает вопрос: насколько статистически значимо это улучшение? В этих случаях обычно применяют несколько модифицированный критерий Фишера – сравнивают улучшение с оценкой дисперсии более простой модели. Если обозначить за n число экспериментальных данных, m₁ и m₂ число параметров в моделях (m₂> m₁), то сначала считаются остаточные суммы квадратов для моделей и их улучшение.

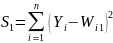
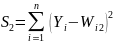
S=S₁-S₂

Затем считаются средние квадраты отклонений (аналоги дисперсии)

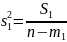
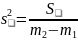
Наконец находится значение отношения улучшения к тому, что было в более простой модели

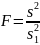
Это значение и сравнивается с табличным для заданных вероятности ошибки и чисел степеней свободы (m₂- m₁ в числителе, n-m₁ в знаменателе). Если мы получили величину большую табличной, значит улучшение значимое и есть смысл использовать более сложную модель. В противном случае лучше ограничиться более простой.

На последок нужно заметить, что человечество напридумло уже огромное множество разнообразных критериев. И довольно часто бывает, что один критерий утверждает одно, а другой противоположное. Разбираться в причинах таких явлений часто бывает нелегко. Обычно все списывают на случайность, а для желающих разобраться просто приводят данные расчетов по разным критериям. Поэтому всегда стоит относиться с большим скепсисом к выводам, где значения критериев близки к пороговым значениям.

Лекция 3. Информационная. Объясняются методы оценки роли отдельных переменных в математических моделях двигателей летательных аппаратов. Излагаются методы оценки взаимосвязи отдельных переменных и расчет коэффициента корреляции. Показываются методы оценки адекватности сложной системы по данным об адекватности моделей подсистем.

Проверка адекватности математической модели сложной системы данным об адекватности моделей подсистем.

Теперь поговорим об оценке влияния отдельных переменных. В первую очередь это нужно для того, чтобы создавать модели максимально простыми. То есть учитывать в них то, что необходимо. А от остального по возможности избавляться. Предположим, что у нас есть некий «черный ящик» с большим набором входных параметров. И нам нужно создать по возможности простую его математическую модель. Есть подозрения, что многие входные параметры не влияют (или не существенно влияют) на выходные. Следовательно, в окончательной модели их можно будет не учитывать. Но для этого сначала нужно получить какую-то численную оценку «влиятельности» для каждого параметра.

В большинстве случаев для этих целей ограничиваются линейным приближением. Тогда в качестве численной оценки используется коэффициент корреляции. Однако следует помнить, что в ряде случаев линейные оценки оказываются явно недостаточными. Например, если в одной части диапазона параметр оказывает одно влияние на результат, а в другой противоположное, то в линейном приближении его влияние будет близким к нулю. Даже если на самом деле этот параметр весьма существенен.

Однако вернемся к коэффициенту корреляции. С точки зрения математики это величина, показывающая насколько согласованно меняются две переменные. Коэффициент корреляции изменяется в диапазоне от -1 до 1. Если увеличение (уменьшение) одной переменной всегда приводит к пропорциональному увеличению (уменьшению) другой, то коэффициент должен быть равен 1. Аналогично, если переменные всегда пропорционально изменяются в противоположные стороны, то коэффициент должен быть равен -1. Если переменные независимы, то в результате должны получить 0. В большинстве случаев столь однозначной связи не наблюдается, и коэффициент может приобретать промежуточные значения. Но если переменные чаще меняются в одну сторону, значение должно быть положительным, в разные – отрицательным. Чем более согласованно изменяются переменные, тем больше должен быть модуль коэффициента.

Строго говоря, существуют разные формулы удовлетворяющие перечисленным выше требованиям. Но как правило в литературе приводят только одну.

К этой формуле сходу могу предъявить претензию. Она предполагает, что у распределений обеих переменных есть дисперсия. А это не всегда так. На практике спасает тот факт, что обычно приходится иметь дело с ограниченным дискретным набором значений, а в этом случае дисперсия точно существует. Правда, не стоит забывать, что особо въедливые оппоненты всегда могут потребовать дополнительных обоснований применимости полученных результатов. Единственным эффективным научным способом борьбы с такими оппонетами является накопление очень большого объема статистических данных. Но технари обычно используют более простой способ доказательства: если «железо» построенное по данной модели заработало, значит модель правильная. Этот критерий не является идеальным с точки зрения науки, но зато очень практичен. В качестве примера, где подобных подход оказался несправедлив, можно привести модель термодинамических циклов Сади Карно. Он разработал ее на основе теории флогистона (теплорода), в последтсвии опровергнутой. Тем не менее созданные на основе этой модели тепловые машины (включая и двигатели летательных аппаратов) и по сей день прекрасно работают.

Еще одна важная вещь, о которой всегда нужно помнить при работе с коэффициентами корреляции: они ничего нам не говорят о причинно-следственных связях. То есть даже если коэффициент указывает на высокий уровень корреляции, то этому могут соответствовать самые разнообразные варианты. Например, легко можно предположить, что изменение первой переменной является следствием изменения второй. Но ведь нумерация переменных в данном случае – это наш произвол. То есть с той же степенью уверенности можно утверждать, что причинно-следственная связь прямо противоположная. А может изменения обеих переменных являются следствием чего-то третьего. И это не говоря уже о чисто случайном совпадении.

Тем не менее судить о вероятности наличия связей по коэффициентам корреляции все же можно. И в первом приближении их можно использовать для ранжирования переменных. А по результатам этого ранжирования судить, какие переменные учитывать в модели, а какие нет. Тут мы подошли к еще одной проблеме: где именно подвести черту в списке переменных. Очевидно, что ответ зависит от требуемой точности. Но хочется иметь какую-нибудь формулу. Ее легко получить используя несколько упрощений и предположений. Первым из них идет использование линейного приближения. Тогда конечный результат в модели будет описываться простой формулой

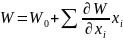
Далее вводим предположение о независимости переменных. Тогда можно получить достаточно простую формулу проделав следующие операции. Возводим приведенную выше формулу в квадрат. Сумму произведений различных производных приравниваем нулю (см. предположение о независимости). И наконец подставим вместо переменных ширину диапазона их изменения.

Если под шириной диапазона мы будем понимать ожидаемую ошибку, то мы получим формулу для оценки погрешности конечного результата через погрешность в отдельных переменных. А из такой формулы можно сделать много полезных выводов. Ранее мы упоминали, что можно оценивать погрешность из-за неучета отдельных процессов. Значит, по этой формуле можно определять где подвести черту в ранжированном списке. А можно зайти с другой стороны. Если у нас задана конечная точность, то по этой формуле можно получить допустимую погрешность определения той или иной переменной. А теперь представьте, что мы имеем дело с какой-то сложной системой (например двигателем). У нас есть модели отдельных его подсистем. Как по ним определить погрешность определения характеристик системы? По этой же формуле. Только теперь будем считать, что переменные описывают не отдельные процессы или параметры, а выходные характеристики подсистем. Отсюда же получаем требования к точности моделей подсистем. А еще ранее упоминалась задача взаимодействия моделей подсистем. То есть если нам говорят, что такую-то подсистему (скажем, насос) можно посчитать лишь с такой то точностью (хуже, чем предполагалось), то по этой же формуле мы можем оценить возможность получения заданной конечной точности за счет ужесточения требований к другим подсистемам.

Практические и семинарские занятия – 4 часа.

Занятие 1. Критерии согласия хи-квадрат и Смирнова-Колмогорова. Критерий Фишера. Форма проведения занятий – решение задач. Отрабатываемые вопросы: оценка адекватности математической модели.

Занятие 2. Оценка адекватности сложной системы по данным об адекватности моделей подсистем. Форма проведения занятий – решение задач. Отрабатываемые вопросы: Оценка адекватности модели двигателя по данным о моделях его элементов.

Управление самостоятельной работой студента 9 часов:

проработка материалов лекций – 4 часа; подготовка к практическим занятиям и анализ результатов полученных в ходе их проведения – 5 часов.