Приложение 3

Матрицы специального вида

Матрица Адамара (Hadamard matrix)

Матрицы Адамара встречаются в различных приложениях – комбинаторике, численном анализе, обработке сигналов. Это матрицы, элементы которых принимают значения 1 или -1, столбцы ортогональны, так что справедливо соотношение:

H’ * H = n * I,

где [n, n] = size(H) и I = eye(n, n).

Матрица Адамара порядка n > 2 существует только тогда, когда n кратно 4. Реализованный алгоритм вычисляет матрицы Адамара для случаев, когда величины n, n/12, n/20 являются двойки.

Синтаксис:

H = hadamard(n) – возвращает матрицу Адамара размерности nxn

Пример.

>> H = hadamard(8)

H =	1	1	1	1	1	1	1	1
	1	-1	1	-1	1	-1	1	-1
	1	1	-1	-1	1	1	-1	-1
	1	-1	-1	1	1	-1	-1	1
	1	1	1	1	-1	-1	-1	-1
	1	-1	1	-1	-1	1	-1	1
	1	1	-1	-1	-1	-1	1	1
	1	-1	-1	1	-1	1	1	-1

Картина линий уровня для этой матрицы напоминает ковер (рис. 1).

>> contour(hadamard(8)) % линии контура

>> pcolor(H) % закрашенные области (палитра summer)

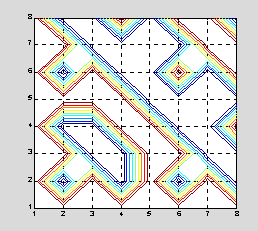
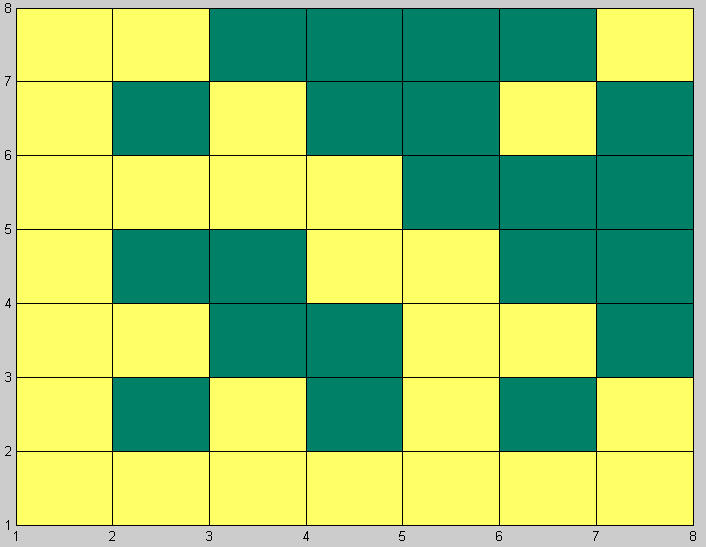
а) б)

Рис. 1 Графическое представление матрицы Адамара

а) линии уровня; б) закрашенные области

Матрица Адамара используется при кодировании информации.

Матрица Ганкеля (Hankel matrix)

Матрица Генкеля – квадратная матрица, у которой на всех диагоналях, перпендикулярных главной, стоят равные элементы.

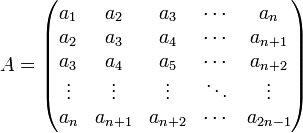
Ганкелевы матрицы полностью определяются элементами , , …, . Эти элементы называются образующими ганкелевой матрицы

Синтаксис:

H = hankel(c) – возвращает квадратную матрицу Генкеля H, которая строится по заданному вектору с Ганкеля, первый столбец которой совпадает с вектором c, а все остальные элементы H(i, j), i + j > n, лежащие ниже второй главной диагонали, равны нулю;

H = hankel(c, r) – возвращает матрицу Ганкеля, первый столбец которой совпадает с вектором c, а последняя строка с вектором r. Если последний элемент вектора c не равен первому элементу вектора r, то возникает конфликт на второй главной диагонали, когда предпочтение отдается элементу вектора c.

Примеры:

1) >> c = [1 2 3 4 5];

>> H = hankel(c) % построение матрицы Ганкеля

H =	1	2	3	4	5
	2	3	4500
	3	4	5	0	0
	4	5	0	0	0
	5	0	0	0	0

Выведем графическое представление матрицы (рис.2):

>> pcolor(H)

>> contourf(H)

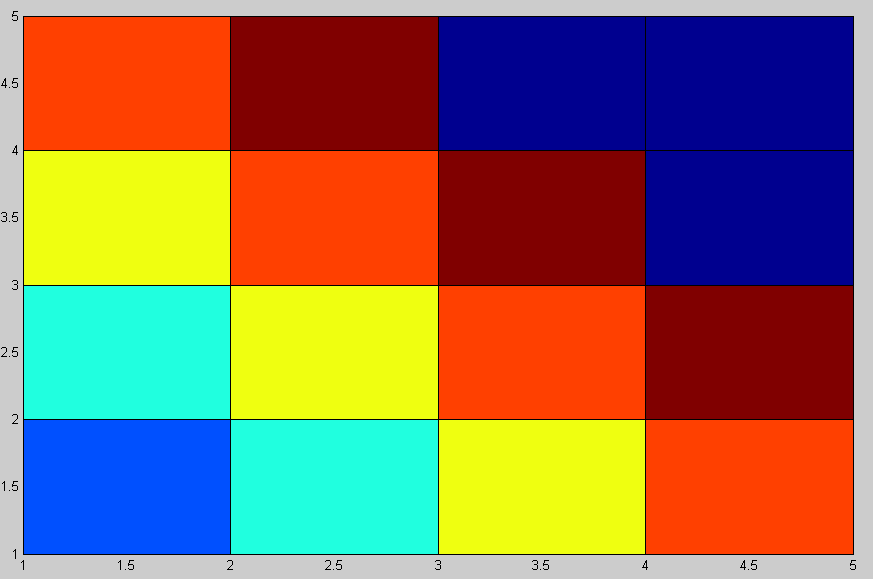
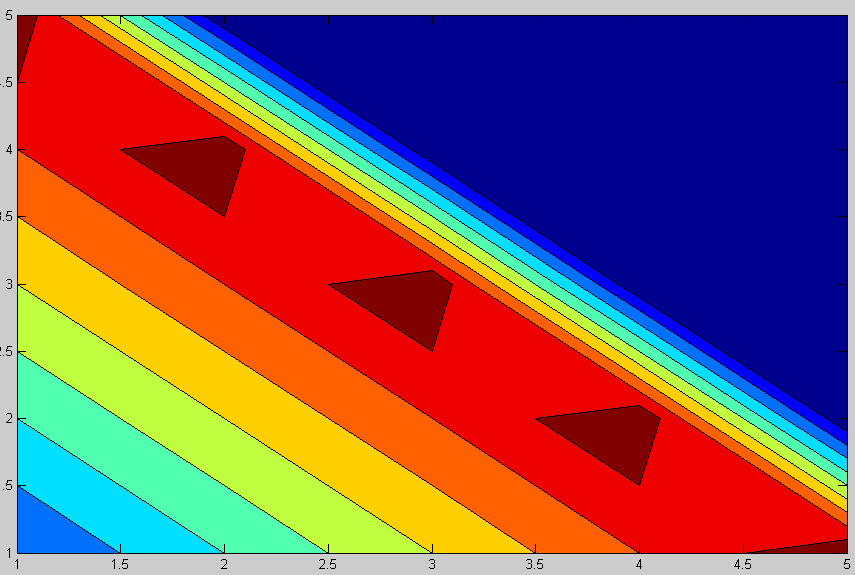
Рис. 2 Графическое представление матрицы Генкеля

2) >> c = 1:3; r = 7:10; H = hankel(c, r)

Warning: Column wins anti-diagonal conflict. – Столбец выигрывает конфликт на второй главной диагонали

> In d:\matlab5\toolbox\matlab\elmat\hankel.m at line 27

H =	1	2	3	8
	2	3	8	9
	3	8	9	0

Матрица Ганкеля используется при локализации и вычислении корней полинома.

Матрица Гильберта (Hilbert matrix)

Матрица Гильберта – это пример очень плохо обусловленной по отношению к операции обращения матрицы. Элементы этой матрицы определяются следующим образом: .

Синтаксис:

H = hilb(n) – формирует матрицу Гильберта порядка n;

H = invhilb(n) – формирует матрицу, обратную матрице Гильберта порядка n. Точная обратная матрица – это матрица, элементами которой являются целые числа. Точное представление такой матрицы в арифметике с плавающей точкой возможно только тогда, когда порядок матрицы не превышает 13. Для больших значений n функция invhilb формирует только приближенную матрицу.

Пример.

Матрица Гильберта порядка 4 имеет число обусловленности 1.5514e+004.

>> hilb(4)

ans =	1.0000	0.5000	0.3333	0.2500
	0.5000	0.3333	0.2500	0.2000
	0.3333	0.2500	0.2000	0.1667
	0.2500	0.2000	0.1667	0.1429

Ее обратная матрица – это целочисленная матрица вида:

>> invhilb(4)

ans =	16	-120	240	-140
	-120	1200	-2700	1680
	240	-2700	6480	-4200
	-140	1680	-4200	2800

а результат обращения в арифметике с плавающей точкой

>> format long e,     inv(hilb(4))

           1.0e+ 003*

ans =	0.0160	-0.1200	0.2400	-0.1400
	-0.1200	1.2000	-2.7000	1.6800
	0.2400	-2.7000	6.4800	-4.2000
	-0.1400	1.6800	-4.2000	2.8000

На графическом представлении матрицы Гильберта видно, что диапазон изменения значений очень велик (рис. 3).

>> pcolor(hilb(4))

>> contourf(hilb(4))

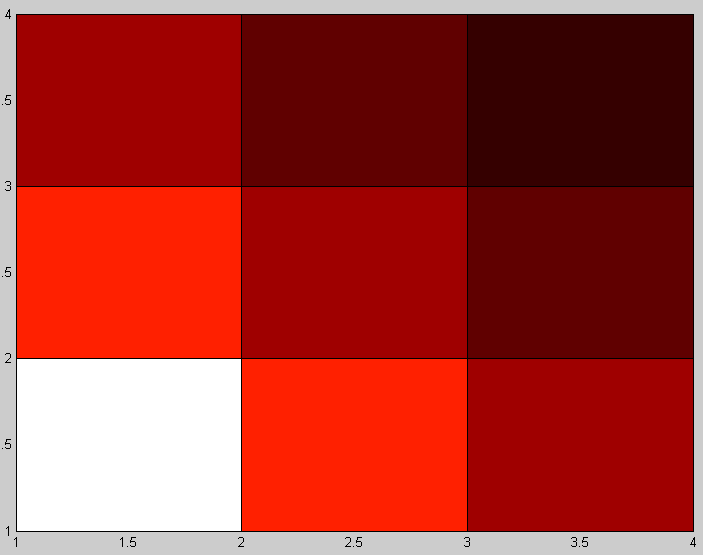
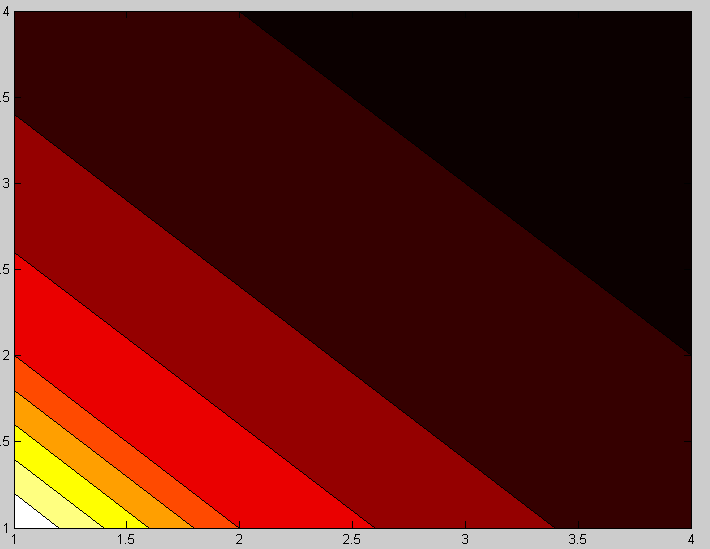
Рис. 3 Графическое представление матрицы Гильберта

Магический квадрат

Магический квадрат представляет собой матрицу, у которой сумма всех строк и столбцов одинакова. Сумму элементов по строкам (столбцам) называют инвариантом магического квадрата и обозначают mn. Значение инварианта зависит от n и равно m_n = n(n² +1)/2.

Синтаксис:

M = magic(n) –для n > 3 формирует специальную квадратную матрицу порядка n, элементами которой являются целые числа от 1 до n2, суммы элементов которой по строкам и столбцам равны.Значение суммы называется инвариантом магического квадрата.

Если матрицу магического квадрата ортонормировать делением на ее инвариант, то получим дважды стохастическую матрицу, обладающую тем свойством, что ее матричная норма любого порядка равна 1.

Ранг матрицы M зависит от n следующим образом:

График функции rank(magic(n)) для 3 <= n< = 32 показан на рис. 4:

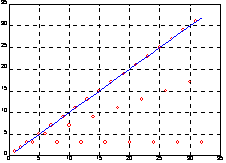
Рис. 4 Графическое представление ранга магического квадрата

С магическими квадратами связано много легенд. Самый древний магический квадрат обнаружен в надписи ХI века в индийском городе Кхаджурахо (рис. 5а)), а самый известный – изображен на гравюре Альбрехта Дюрера «Меланхолия I» и считается самым ранним в европейском искусстве (рис. 5б)).

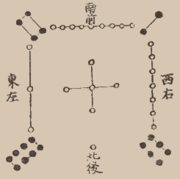
а) б)

Рис. 5 Исторические магические квадраты

Дьявольским магическим квадратом называют квадрат у которого также с магической константой совпадает сумма чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях (рис. 6). Такие магические квадраты еще называются пандиагональными.

3 61 19 37 43 31 5 41 7 11 73 29 67 17 23 13		1	15	24	8	17
		9	18	2	11	25
		12	21	10	19	3
		20	4	13	22	6
		23	7	16	5	14

Рис. 6 Дьявольские магические квадраты