
- •Пояснительная записка.
- •Тематика вопросов для самостоятельного изучения самостоятельные работы
- •Тема 1.1 Действительные числа. Приближенные вычисления и вычислительные средства.
- •Тема 1.2 Уравнения и неравенства первой и второй степени.
- •Тема 1.3 Определители.
- •Тема 2.1 Последовательности. Предел последовательности.
- •Тема 2.2 Числовая функция. Ее свойства и график.
- •Тема 2.3. Предел функции.
- •Тема 3.1.Степень и ее свойства.
- •Тема 3.2.Логарифмы и их свойства.
- •Тема 3.3.Показательная, логарифмическая и степенная функции, их свойства и график
- •Тема 3.4.Показательные и логарифмические уравнения и неравенства
- •Тема 4.1.Тождественные преобразования.
- •Тема 4.2.Свойства и графики тригонометрических функций.
- •Тема 4.3.Тригонометрические уравнения и неравенства.
- •Тема 5.1 Производная функции.
- •Тема 5.2. Исследование функций с помощью производной.
- •Тема 6.1 Неопределенный интеграл.
- •Тема 6.2. Определенный интеграл.
- •Тема 7.1. Действия над векторами.
- •Тема 8.1. Начальные понятия стереометрии. Взаимное расположение прямых и плоскостей в пространстве.
- •Тема 8.2. Двугранные углы.
- •Тема 9.1. Многогранники. Площадь поверхности многогранников.
- •Тема 9.2 Тела вращения. Площадь поверхности тел вращения.
- •Тема 10.1 Объемы геометрических тел.
- •Приложения
- •Характеристика заданий
- •4. Содержание и оформление опорных конспектов.
Тема 4.2.Свойства и графики тригонометрических функций.
Цель: углубление и систематизация знаний.
Форма работы: модель тригонометрического круга, опорный конспект
Задания для самостоятельной работы:
№1. Изготовить модель тригонометрического круга на плотной бумаге формата А4. Показать линии тангенса и котангенса.
№2. Составить опорный конспект по теме «Графики обратных тригонометрических функций».
Список рекомендуемой литературы:
1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
2. Мордкович А.Г., Алгебра и начала анализа, 10-11 классы, часть 1, М.: Мнемозина, 2007.
3.БашмаковМ.И.,Алгебра и начала анализа, 10-11 классы, М.: Просвещение, 1993.
Порядок проверки, защиты самостоятельной работы: опрос, проверка рабочей тетради.
Тема 4.3.Тригонометрические уравнения и неравенства.
Цель: развитие навыков по сбору, систематизации, переработке и оформлению информации, отработать основные приемы решения тригонометрических уравнений и неравенств.
Форма работы: Формирование информационного блока, решение задач.
Задания для самостоятельной работы:
Вариант 1.
№1. Сформировать информационный блок по теме «Решение тригонометрических уравнений и неравенств».
№2. Вычислить:
1)
 ;
;
2)
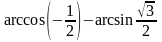 ;
;
3)
 .
.
№3. Решить уравнение:
1)
 ;
2)
;
2)
 ;
3)
;
3)
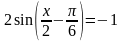 ;
4)
;
4)
 ;
5)
;
5)
 .
.
№4.Решить систему
уравнений:
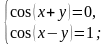
№5. Решить неравенство:
1)
 ;
2)
;
2)
 ; 3)
; 3)
 ;
;
4)
 ;
5)
;
5)
 .
.
№6.
Решить уравнение
 и
найти его корни, принадлежащие отрезку
и
найти его корни, принадлежащие отрезку
 .
.
Вариант 2.
№1. Сформировать информационный блок по теме «Решение тригонометрических уравнений и неравенств».
№2. Вычислить:
1)
 ;
;
2)
 ;
;
3)
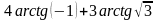 .
.
№3. Решить уравнение:
1)
 ;
2)
;
2)
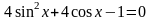 ;
3)
;
3)
 ;
;
4)
 ;
5)
;
5)
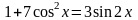 .
.
№4.Решить
систему уравнений

№5. Решить неравенство:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
;
4)
 ;
5)
;
5)
 ;
;
№6.
Решить уравнение
 и
найти его корни, принадлежащие отрезку
и
найти его корни, принадлежащие отрезку
 .
.
Список рекомендуемой литературы:
1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
2. Мордкович А.Г., Алгебра и начала анализа, 10-11 классы, часть 1, М.: Мнемозина, 2007.
3.БашмаковМ.И.,Алгебра и начала анализа, 10-11 классы, М.: Просвещение, 1993.
Порядок проверки, защиты самостоятельной работы: проверка рабочей тетради.
Тема 5.1 Производная функции.
Цель: отработать навыки вычисления производных функций, развивать умения применять полученные знания при решении физических задач.
Форма работы: тестирование
Задания для самостоятельной работы:
Вариант 1.
№1. Написать реферат на тему «Применение производной»
№2. Выполнить тест по теме «Производная».
1.
Производная функции
![]() равна:
равна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
2. Производная
функции
![]() в точке х=-1
равна:
в точке х=-1
равна:
а) –1,5; б) 1,5; в) –0,75; г) 0,75.
3.
Какая из приведенных функций является
производной функции
![]() ?
?
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
4. Уравнение
касательной к графику функции
![]() в
точке с абсциссой х0
= -3
имеет вид:
в
точке с абсциссой х0
= -3
имеет вид:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
5. Тело
движется по прямой так, что расстояние
S
(в метрах)
от него до точки B
этой прямой изменяется по закону
![]() (t
– время движения в секундах). Через
сколько секунд после начала движения
мгновенная скорость тела будет равна
72 м/с.
(t
– время движения в секундах). Через
сколько секунд после начала движения
мгновенная скорость тела будет равна
72 м/с.
а) 16; б)15; в) 14; г) 13.
6. На
рисунке изображён график
производной
некоторой функции
![]() ,
заданной на промежутке ( - 3; 3). Сколько
точек максимума имеет функция
,
заданной на промежутке ( - 3; 3). Сколько
точек максимума имеет функция
![]() на
этом промежутке?
на
этом промежутке?

7.
Найдите угловой коэффициент касательной
к графику функции
![]() в точке
в точке
![]() .
.
8.Найдите производные функций:
а)
![]() ;
б)
;
б)
![]() .
.
9*.
Найдите
сумму тангенсов углов наклона
касательных к параболе
![]() в точках пересечения параболы с осью
абсцисс.
в точках пересечения параболы с осью
абсцисс.
Вариант 2.
№1. Написать реферат на тему «Применение производной».
№2. Выполнить тест по теме «Производная».
1. Производная
функции
![]() равна:
равна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
2. Производная
функции
![]() в точке х=1
равна:
в точке х=1
равна:
а) 1,2; б) 2; в) –1,2; г) 2,5.
3. Какая из
приведенных функций является производной
функции
![]() ?
?
а)
![]() ;
б)
;
в)
;
б)
;
в)
![]() ;
г)
;
г)
![]() .
.
4.
Уравнение
касательной к графику функции
![]() в
точке с абсциссой х0
= -3
имеет вид:
в
точке с абсциссой х0
= -3
имеет вид:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
5. Тело
движется по прямой так, что расстояние
от начальной точки изменяется по
закону
![]() (м),
где t
– время движения в секундах. Найдите
скорость тела через 10 секунд после
начала движения .
(м),
где t
– время движения в секундах. Найдите
скорость тела через 10 секунд после
начала движения .
1) 10; 2) 9; 3) 8; 4) 7.
6. На рисунке изображён график производной некоторой функции , заданной на промежутке ( - 2; 2). Сколько точек минимума имеет функция на этом промежутке?

7.
Найдите угловой коэффициент касательной,
проведенной к графику функции![]() в точке
в точке
![]() .
.
8.Найдите производные функций:
а)
![]() ;
б)
;
б)
![]() .
.
9*.
Найдите
сумму угловых коэффициентов касательных
к параболе
![]() в точках пересечения параболы с осью
абсцисс.
в точках пересечения параболы с осью
абсцисс.
Список рекомендуемой литературы:
1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
2. Мордкович А.Г., Алгебра и начала анализа, 10-11 классы, часть 1, М.: Мнемозина, 2007.
3.БашмаковМ.И.,Алгебра и начала анализа, 10-11 классы, М.: Просвещение, 1993.
Порядок проверки, защиты самостоятельной работы: проверка рабочей тетради.
