Тема 2.2 Числовая функция. Ее свойства и график.
Цель: уметь по графику функции определить ее свойства; уметь строить графики функций.
Форма работы: тестирование
Задания для самостоятельной работы:
Вариант 1.
1. По графику функции
,
изображенному
на рисунке, определите промежуток
убывания функции:
1)
|
2)
|
3)
|
4)
|
;
;
;
.2. По графику функции , изображенному на рисунке, определить максимум и минимум функции.
3. По графику функции , изображенному на рисунке указать область определения и область значения функции.
4. По
графику функции
,
изображенному на рисунке, указать
промежутки, где
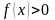
5. Найти область
определения функции
.
1)
|
2)
|
3)
|
4) . |
;
;
;
6. Укажите
наибольшее значение функции
на отрезке
.
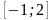1) -12; |
2) 8; |
3) -6; |
4) -2. |
7. При каких значениях
х
функция
принимает положительные значения?
1)
|
2)
|
3)
|
4)
|
;
;
;
.
8. Найдите нули
функции
.
1)
|
2)
|
3)
|
4)
|
;
;
;
.
9. Постройте график
функции:
.
Вариант 2.
1. По графику функции , изображенному на рисунке, определите промежуток возрастания функции:
1) ; |
2)
|
3)
|
4) . |
;
;
2. По графику функции , изображенному на рисунке, определить максимум и минимум функции.
3. По графику функции , изображенному на рисунке указать область определения и область значения функции.
4. По графику функции , изображенному на рисунке, указать промежутки, где .
5. Найти область
определения функции
.
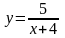1)
|
2)
|
3)
|
4) . |
;
;
;
6.
Укажите
наименьшее значение функции
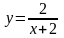на отрезке
.
1) -1; |
2) -0,5; |
3) 1; |
4) 0,5. |
7.
При каких
значениях
функция
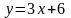принимает
отрицательные значения?
1) ; |
2)
|
3)
|
4)
|
;
;
.8.
Найдите нули
функции
.
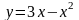1)
|
2) ; |
3)
|
4)
|
;
;
.9.
Постройте график функции:
.
Список рекомендуемой литературы:
1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
2. Мордкович А.Г., Алгебра и начала анализа, 10-11 классы, часть 1, М.: Мнемозина, 2007.
3.БашмаковМ.И.,Алгебра и начала анализа, 10-11 классы, М.: Просвещение, 1993.
4. Пратусевич М.Я., Алгебра и начала анализа. 10 класс, учеб. для общеобразоват. учреждений, М.: Просвящение, 2009.
Порядок проверки, защиты самостоятельной работы: проверка рабочей тетради.
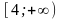
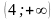
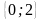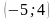
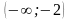
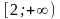