Тема 7.1. Действия над векторами.

Цель: систематизация и закрепление знаний и практических умений, развитие способности выделять главные понятия темы и формулировать их.

Форма работы: составление глоссария, решение задач,

Задания для самостоятельной работы:

Вариант 1.

№1. Составить глоссарий по теме «Вектор».

№2. При каких значениях длины векторов и

будут равны?

№3. Вычислить угол между векторами и .

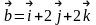№4.Определить угол между векторами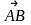 и , если А (1; -3; -4),

В (-1; 0; 2), С (2; -4; -6), D (1; 1; 1).

№5. Найти равнодействующую двух сил и , если 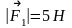, , угол между ними

Вариант 1.

№1. Составить глоссарий по теме «Вектор».

№2. Даны векторы и .При каком значении m .

№3. Вычислить угол между векторами и .

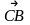№4.Определить угол между векторами и , если А (1; 3; 0),

В (2; 3; -1), С (1; 2; -1).

№5.Вычислить работу, которую производит сила , если ее точка приложения, двигаясь прямолинейно, перемещается из положения А (-1; 3), в положение В (3; 4).

Список рекомендуемой литературы:

1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. Атанасян А. С., Бутузов В.Ф., Кадомцев С.Б., Геометрия 10-11, М: Просвещение, 2010.

Порядок проверки, защиты самостоятельной работы: проверка рабочей тетради.

Тема 8.1. Начальные понятия стереометрии. Взаимное расположение прямых и плоскостей в пространстве.

Цель: систематизировать знания и умения по данной теме, развивать интерес к предмету.

Форма работы: подготовка реферата.

Задания для самостоятельной работы:

№1.Написать реферат на одну из тем:

1. Взаимное расположение двух прямых в пространстве (формулировки и примеры).

2. Взаимное расположение двух плоскостей (формулировки и примеры).

3. Взаимное расположение прямой и плоскости в пространстве (формулировки и примеры).

4. Свойства параллельных плоскостей (формулировки и примеры).

5. Перпендикуляр и наклонная к плоскости (формулировки и примеры).

6. Угол между прямой и плоскостью (формулировка и примеры).

7. Задачи по теме "Взаимное расположение прямых и плоскостей в пространстве».

8. История возникновения стереометрии.

9. Плоскость и прямая (историческая справка).

10. Основоположники стереометрии.

Список рекомендуемой литературы:

1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. Атанасян А. С., Бутузов В.Ф., Кадомцев С.Б., Геометрия 10-11, М: Просвещение, 2010.

Порядок проверки, защиты самостоятельной работы: защита реферата.

Тема 8.2. Двугранные углы.

Цель: повторение и закрепление темы, выработка умений и навыков по решению задач, развитие конструктивных навыков нахождения угла между плоскостями и пространственного воображения студентов

Форма работы: решение задач.

Задания для самостоятельной работы:

Вариант 1.

№1.В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁, у которого AB=6, CC₁=4, найдите тангенс угла между плоскостями ACD₁ и A₁B₁C₁.

№2. Найдите площадь полной поверхности правильной треугольной пирамиды, если сторона ее основания равна 6,а двугранный угол при основании равен 60⁰.

№3. В правильной треугольной пирамиде SABC с основанием ABC известны ребра: AB=5√3, SC=13. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.

Вариант 2.

№1. В правильной треугольной призме ABCA₁B₁C₁ высота равна 2, сторона основания равна 1. Найдите расстояние от точки B₁ до прямой  AC_1.

№2. Дана правильная треугольная призма ABCA₁B₁C₁, сторона основания которой равна 2, диагональ боковой грани . Найти угол между плоскостью A₁BC и плоскостью основания призмы.

№3. Сторона основания правильной треугольной призмы ABCA₁B₁C₁ равна 2, а диагональ боковой грани равна . Найдите угол между плоскостью A₁BC и плоскостью основания призмы.

Список рекомендуемой литературы:

1.Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. Атанасян А. С., Бутузов В.Ф., Кадомцев С.Б., Геометрия 10-11, М: Просвещение, 2010.

Порядок проверки, защиты самостоятельной работы: проверка рабочей тетради.